
次のページ
前のページ
目次
CAN-1-1-2
TEC-0-1-7
TEC-0-1-8
TEC-0-1-27
TEC-0-1-28
TEC-0-1-29
TEC-0-1-30
TEC-0-1-31
TEC-0-1-32
TEC-0-1-33
TEC-0-1-34
TEC-0-1-35
TEC-0-1-36
TEC-0-1-37
TEC-0-1-39
【補足説明欄】
1行目の [強制力を受ける減衰振動系] は、2~5行目の記事のタイトルです。2014.12.04
2行目の「先述の減衰振動系」とは、CAN-1-1-12-20~24で扱われている質点と力の法則の事です。2014.12.04
2行目の f とωは、両方とも正の実定数です。
このωは、TEC-0-1-25-5,6のωとは関係ありません。2014.12.04
2行目の外力の式に m が含まれている事についても、CAN-1-1-12-26の外力の式に m が含まれている事についての補足説明と、同様の事が言えます。2014.12.08
2行目の外力について、COM-1-12に補足説明が書かれています。2014.12.04
4行目の式の立式の根拠は、以下です。
F = -kxi -c(dx/dt)i + mf cos(ωt)i ∵CAN-1-1-4-4; CAN-1-1-12-20,21; CAN-1-1-13-2
= [-kx -c dx/dt + mf cos(ωt)]i
これとTEC-0-1-7-8から、
F1 = -kx -c dx/dt + mf cos(ωt)
F2 = 0
F3 = 0
これをTEC-0-1-7-21に代入すると、
m d2x/dt2 = -kx -c dx/dt + mf cos(ωt)
m d2y/dt2 = 0
m d2z/dt2 = 0
この方程式は明らかに、y = z = 0 の範囲内に解を持ちます。
y = z = 0ではない解も勿論ありますが、探索範囲をy = z = 0である様な解に限定する事が、CAN-1-1-13-2の「先述の減衰振動系に」という言葉と、CAN-1-1-12-21,22の「x軸上を運動する場合」という言葉によって、表現されています。2014.12.04,08
5行目のω0は、CAN-1-1-12-29のω0です。2014.12.04
5行目の式を微分方程式と見て解く事は、TEC-0-1-27-9~26で行われています。2014.12.04
6行目の「③中心力」は、CAN-1-1-13-7~CAN-1-1-14-8の記事のタイトルです。2014.12.09
7行目の [一般論] は、8~19行目の記事のタイトルです。2014.12.09
8行目の問題設定は、COM-1-5-11,12の理解に則っています。
ここで用いられている記号 f' には、「f の微分」という意味は有りません。
17,18行目の f と区別するために、f' という記号を用いました。
r,θ,φは、CAN-1-1-2-22~27で定義されている空間極座標です。
er は、CAN-1-1-2-22~27で定義されている方向ベクトルです。2014.12.09;2015.07.16
10,11行目の左の等号の成立根拠は、積の微分法です。2014.12.09
10,11行目の右の等号の成立根拠は、以下の2点です。
(dr/dt)×m(dr/dt) = 0 ∵同じ向きのベクトル同士の外積はゼロベクトル
m d2r/dt2 = F(r) ∵CAN-1-1-4-6;CAN-1-1-1-8,9
= f'(r,θ,φ)er ∵CAN-1-1-13-8
これら2点に留意すると、
(dr/dt)×m(dr/dt) + r×md2r/dt2
= 0 + r×f'(r,θ,φ)er
= f'(r,θ,φ)r×er
という風に計算できます。2014.12.09;2015.07.16
12行目の等号の成立は、er と r の向きが同じである事(CAN-1-1-3-1)と、同じ向きのベクトル同士の外積はゼロベクトルである事に、依ります。2014.12.09;2015.04.02
13,14行目に書かれている r が r×m(dr/dt) に垂直である事は、外積の定義から言える事です。
ベクトルAとベクトルBの外積A×Bは、AとBの両方に垂直なベクトルとして定義されていますね。2014.12.09;2015.04.05;2015.07.17
16行目の「TEC-0-1-7-28~8-6」は、TEC-0-1-7-28からTEC-0-1-8-6まで、という意味です。2015.04.05;2015.07.16
17,18行目の式の立式では、z軸の正の向きが r×m(dr/dt) の向きに一致する様な座標系を用いています。
r×m(dr/dt) がどんな向きのベクトルであっても、その様な座標系が存在する事は明らかです。
文献によっては、この事を「r×m(dr/dt) の向きはz軸の正の向きに一致すると仮定しても一般性を失わない」という言い方で表現している場合が、多分あると思います。
ベクトルを限定せずそれに合わせて座標系を選ぶのが本当ですが、その事を、ベクトルを限定するかの様な(良く見ると、ベクトルと座標系の関係を限定しているだけで、ベクトルを限定しているわけではないのだけれど)言い方で表現するわけです。
(いつでも出来る)=(一般的だ) という認識に立脚した表現です。
「一般性」という言葉のこの様な使い方を知っておく事は、当典以外の文献を読むためには必要です。
さて、この様な座標系を用いた場合、平面極座標(CAN-1-1-2-9~14)と空間極座標(CAN-1-1-2-22~27)を見比べる事によって、
(空間極座標のer) = (平面極座標のer)
(空間極座標の r) = (平面極座標の r)
(空間極座標のφ) = (平面極座標のθ)
(空間極座標のθ) = π/2
だと分かるので、TEC-0-1-7-29とCAN-1-1-13-8から、平面極座標では、
Fr = f'(r, π/2, θ)
Fθ = 0
F3 = 0
だと分かります。
ここで、f'(r, π/2, θ) を f(r, θ) と書く(TEC-0-1-28-15)事にすると、
Fr = f(r, θ)
これらをTEC-0-1-8-5,6の式に代入すると、CAN-1-1-13-17,18の式が得られます。2014.12.09,10;2015.04.05;2015.07.16,17
20行目の [逆2乗中心力] は、21~25行目の記事のタイトルです。
この問題は初等力学の顔です。
それは、この問題を解いた結果のTEC-0-1-29~TEC-0-1-35の中の[場合I][場合II][場合III]が太陽系の惑星の運動についてのケプラーの法則(観測結果)に一致するからです。
この一致は、ニュートンの運動方程式(CAN-1-1-4-6)と万有引力の法則(CAN-1-1-18-18~22)が正しい事の証拠と見なされました。
TEC-0-1-29~TEC-0-1-35の中の[場合IV][場合V]は彗星の運動に一致すると考えられています。2014.12.09;2019.07.05
21,22行目の式を見ると「逆2乗じゃなくて逆3乗じゃん」と思うかもしれませんが、力の大きさは
|F(r)| = |Z|・|r|/|r|3 = |Z|/|r|2
だから「逆2乗」という認識で間違っていません。
r/|r| は、向きがrと同じで長さが1のベクトル(方向ベクトルとか単位ベクトルと呼ばれる)です。
これをnと書けば、
F(r) = (Z/|r|2)n
この様に書くと、F(r)は大きさが |Z|/|r|2 で向きが Z > 0 なら n, Z < 0 なら -n だという事が分かり易い。2019.07.05,06
23行目の左の式は、17,18行目の左の式に、
f(r,θ) = Z/r2
を代入する事によって、得られます。
f(r,θ) = Z/r2
である事と、8~19行目の一般論の適用範囲内である事は、
F(r) = Zr/|r|3
= (Z/|r|2)r/|r|
= (Z/r2)er ∵|r| = r(CAN-1-1-2-22~27), er = r/r(CAN-1-1-3-1)
という風に計算した後で、この計算結果とCAN-1-1-13-8の式を比較して、
f'(r,θ,φ) = Z/r2
∴ f(r, θ) = f'(r, π/2, θ) = Z/r2
という風に考えれば、分かります。2014.12.09;2015.04.05;2015.07.16
23行目の右の式の成立根拠は、17,18行目の右の式です。
hは任意定数です。2014.12.09;2015.04.05
24行目の初期条件中の a と h は、正の任意定数です。2015.07.16
24行目の初期条件中の、
t = 0 で dθ/dt = h/a2
という部分は、
r2dθ/dt = h (23行目)
である事と、初期条件中の
t = 0 で r = a
という部分から導き出されます。2015.07.16,17
24行目の初期条件中の、
t = 0 で θ= 0, dr/dt = 0, r > 0
という部分は、t = 0での位置がx軸の正の部分内にある事と、その時の速度ベクトルがx軸に垂直である事を意味します。
この様に決めても一般性を失わないのか、という問題意識を持つべきですが、その点については、この問題の解に限って言えば失わない、というのが答えです。
しかし、それは解を全て求めた後でないと確認できない事だから、出発点としてこの初期条件を置いた事は、一般性への配慮の観点から言うと、マグレ当たりです。2014.12.14;2015.04.05;2015.07.17
24行目の初期条件中の、
t = 0 で dθ/dt > 0
という部分(hの値が正に限定されている事)は、17,18行目に対する補足説明における座標系と、z軸の正の向きが逆の座標系のどちらかを選択的に採用すれば、常に成立させる事が出来るので、一般性を損なわない条件です。
h = 0 の場合にはそうは言えませんが、h = 0 の場合は、興味深くないという理由で除外してあります。
その分だけ、一般性が損なわれています。
23行目の式に h = 0 を代入すれば、h = 0 の場合の解を求める事は簡単です。
a = 0 の場合を除外したのは、r = 0 での F(r) の値が存在しないからです。2015.04.05;2015.07.16,17
24,25行目の問題は、TEC-0-1-29~TEC-0-1-35で、解かれています。2014.12.09
26行目の [散乱] は、CAN-1-1-13-26~CAN-1-1-14-8の記事のタイトルです。2014.12.09
26行目の「逆2乗中心斥力の場合」とは、20~25行目の問題で Z > 0 とした場合の事です。
従って、TEC-0-1-30-18~21により、この場合を調べるに当たっては、TEC-0-1-29~TEC-0-1-35の内容の中の、一般論の部分と、VIIに該当する部分を、引用する事が出来ます。
「斥力」は、引力と逆向きの力です。2015.11.05,30
27行目の内容は、
| t → +∞ で θ(t) → θ+ とし、t → -∞ で θ(t) → θ- とすると、 散乱角φは、φ≡π- (θ+ - θ-) という式で定義される |
この様子は、CAN-1-1-14-2~8で図解されています。
この定義は、逆2乗中心斥力以外の斥力による散乱についても、適用されます。2015.11.05,16
28行目で定義されている衝突径数bの意味は、CAN-1-1-14-2~8で図示されています。
CAN-1-1-13-28の定義式とCAN-1-1-14-2~8の図中のbの関係は、下図を参考にすれば分かります。
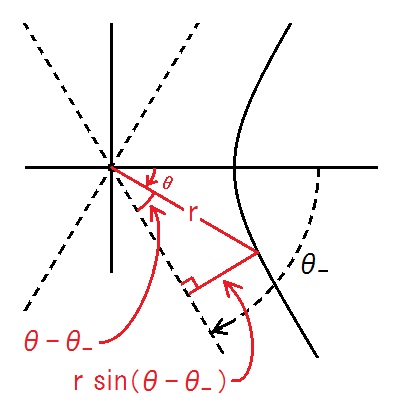
この衝突径数の定義は、逆2乗中心斥力以外の斥力による散乱についても、適用されます。2015.11.05,16,25
28~30行目については、TEC-0-1-37-26~30にも、補足説明が書かれています。2015.11.05
30行目の内容は、TEC-0-1-39-3~7で図解されています。2015.11.06
逆2乗中心斥力による散乱の微分断面積を求める事は、TEC-0-1-36-2~TEC-0-1-37-16で行われています。2015.11.16
【SEOテキスト】宇田雄一,03.10.5,第2章,質点の力学,[強制力を受ける減衰振動系],先述の減衰振動系に、さらに外力 mf cos(ωt)i が働く場合の質点の運動を求めよ。,m,=-kx-c,+mf cos(ωt),y=z=0,∴,+2μ,+(ω0)2x=f cos(ωt),μ=c/(2m),③中心力,[一般論],力の法則がF(r)=f'(r,θ,φ)erの形で与えられる場合、この力を中心力と呼ぶ。この場合、,d,-,dt,[r×m,]=,×m,+r×m,=f'(r,θ,φ)r×er=0,∴r×m,は定ベクトルであり、rはそのベクトルに垂直な定平面内に存し続ける。したがって平面極座標CAN-1-1-2-8~20を用いる事ができ、TEC-0-1-7-28~8-6より、,m(,-r,2)=f(r,θ),m,-,r,d,-,dt,(r2,)=0,とおく事ができ、r2,が一定となる事が分かる。,[逆2乗中心力],F(r)=Z,r,-,|r|3,の場合,m(,-r,2)=Z/r2,r2,=hとおける。,t=0でθ=0,=0,r=a>0,=h/a2>0として運動方程式を解け。,[散乱]逆2乗中心斥力の場合,散乱角φ≡π-(θ+-θ-),θ+≡θ(t→+∞),θ-≡θ(t→-∞),衝突径数b≡lim,t→-∞,r(t) sin[θ(t)-θ-],微分断面積σ≡2πb|db|/[2π(sinφ)|dφ|]