
次のページ
前のページ
目次
CAN-1-1-13
CAN-1-1-14
TEC-0-1-36
TEC-0-1-39
【補足説明欄】
1,2行目の等号の成立根拠は、TEC-0-1-36-28,29の計算結果と、TEC-0-1-34-28,29の式です。
TEC-0-1-34-28,29の式から、
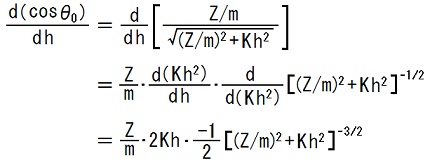
だと分かります。
この計算結果と、
dθ0/d(cosθ0) = 1/[d(cosθ0)/dθ0] = 1/(-sinθ0)
という計算の結果を、TEC-0-1-36-28,29の式に代入すると、TEC-0-1-37-1,2の式が得られます。2015.11.16,30
3,4行目の等号の成立根拠は、TEC-0-1-36-10,11に対する補足説明と同様です。
ここでは、sinθ0 = √[1 - (cosθ0)2] である事と、TEC-0-1-34-28,29の式を、使っています。2015.11.16,30
7,8行目の左の等号の成立根拠は、CAN-1-1-13-30の式です。2015.11.16
7,8行目の右の等号の成立根拠は、TEC-0-1-36-26,27の式と、TEC-0-1-37-1〜6の計算結果です。
db/dφ = (db/dh)/(dφ/dh)
という風に考えます。
絶対値記号を外す時に、
m > 0 (CAN-1-1-4の補足説明欄)
Z > 0 (CAN-1-1-13-26に対する補足説明)
K > 0 (TEC-0-1-30-18〜30VII)
である事を、使っています。2015.11.16,30
9,10行目の最も左の等号の成立根拠は、φ = π - 2θ0(TEC-0-1-36-2,3)です。2015.11.16,30
9,10行目の最も右の等号の成立根拠は、三角関数の倍角の公式です。2015.11.16,30
11,12行目の等号の成立根拠は、TEC-0-1-36-10,11に対する補足説明と同様です。
ここでは、sinθ0 = √[1 - (cosθ0)2] である事と、TEC-0-1-34-28,29の式を、使っています。2015.11.16,30
15,16行目の式の成立根拠は、7,8行目の式と、
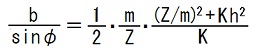
である事です。
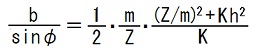
の成立は、9〜14行目の計算結果とTEC-0-1-36-4〜25の計算結果から分かります。2015.11.16;2016.02.01
15,16行目の微分断面積を使うと、全断面積(30行目の内容に対する補足説明)が無限大に成る事は、次の様にして、示されます。
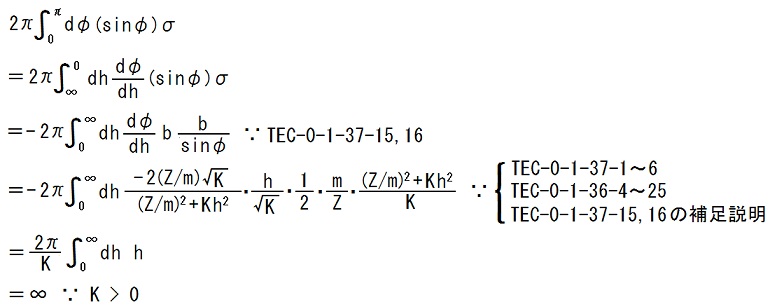
bは定数ではなくφの関数なので、
2π∫0π dφ (sinφ)σ = 2πb2∫0π dφ (1/sinφ) > 2πb2∫0π dφ (1/φ) = ∞
という風に計算するのは間違いです。2015.11.17;2016.02.01
15,16行目についての補足説明が、TEC-0-5-114-24〜TEC-0-5-115-7に、有ります。2015.11.30
第 19 行目の「範単」は「簡単」の誤りです。
19行目の式 r2dθ/dt = h は、TEC-0-1-29-8の式です。2015.11.25
20行目の最も左の等号の成立根拠は、TEC-0-1-29-13,14の式です。2015.11.25
20行目の式 vb = r2dθ/dt の成立は、22,23行目のvの定義を読んだ上で、CAN-1-1-14-2〜8の図で、面積速度(CAN-1-1-3-15〜24)が (1/2)vb であると同時に (1/2)r2dθ/dt でもある事(CAN-1-1-3-23,24)、を見極めれば分かります。
面積速度が (1/2)vb である事は、面積速度が一定である事(TEC-0-1-37-19)に依拠して、t → -∞ において、
(1/2)|r×dr/dt| = (1/2)|r||dr/dt|sin(rとdr/dtが為す角)
→ (1/2)rv sin[π- (θ-θ-)] = (1/2)rv sin(θ-θ-)
→ (1/2)vb ∵CAN-1-1-13-28
と成る事を考えれば、分かります。
t → -∞ で (rとdr/dtが為す角) → π- (θ-θ-)
である事は、CAN-1-1-13-28に対する補足説明の図と、t → -∞でdr/dtが破線に平行に成る事から、分かります。2015.11.25,30;2016.02.01
21行目の式 v2 = K の成立は、20行目の最も左の式が t → -∞でも成立し続ける事、から分かります。
t → -∞では、r → +∞ ∵TEC-0-1-35のVIIのグラフ
t → -∞では、dr/dt → |dr/dt| → v ∵TEC-0-1-37-22,23
だからです。2015.11.25
21行目の式 b = h/√K の成立は、
b = h/v ∵ 20行目の式
= h/√K ∵ 21行目の式 v2 = K
という風に考えれば、分かります。2015.11.25
26〜30行目の内容は、TEC-0-1-39-3〜7で図解されています。2015.11.06
28行目の2πb|db|が入射微小断面積を表す事は、TEC-0-1-39-3〜7の図中の左端の黒色でリング形の平面図形の面積を考える事によって、分かります。2015.11.25
29行目の2π(sinφ)|dφ|は、TEC-0-1-39-3〜7の図中の右端の単位球面上のリング形の領域の面積です。2015.11.25
30行目に書かれている事からすれば、2π∫0π dφ (sinφ)σ は、入射断面の中のφ = 0 に成らない領域の面積であるはずだから、どんなに大きなbに対してもφがゼロでない、ような斥力については、この積分は発散する(無限大に成る)はずです。
2π∫0π dφ (sinφ)σ は全断面積と呼ばれます。
逆2乗中心斥力(CAN-1-1-13-26に対する補足説明)の場合にも、全断面積を具体的に計算すると、結果は無限大に成ります。
学生時代の私は、この積分計算を紙に書かず頭の中で有限値に成ると早合点し、これが矛盾ではないのは何故か、という疑問を持っていて、この疑問を何度か対人的に口にしましたが、誰からも(先生からも)納得の行く答えを聞く事は出来ませんでした。
私の勘違いだったわけですが、無限大に成るよ、という指摘にも全く出会いませんでした。
矛盾だと思ってしまう、という方向へ間違えなかったのは、矛盾の存在が結論に成る事は無い、と知っていたからです。
矛盾の存在が結論に成る事は無い、という理屈は、数学の背理法という論法にも現れています。
その後、計算ミスに気付かないまま自分で考えて、矛盾ではない理由が分かった、と感じた事があります。
その時に私が考えた事は、φが力の中心から測った角度ではない事が原因で、この為に、有限球面の中心から測って同一の角度の方向にある面素片を通って出射する散乱が、異なるφとして重複してカウントされ、その事情が有限球面の半径を無限大に持って行く極限においても持ち越されるからだろう、という物でした。
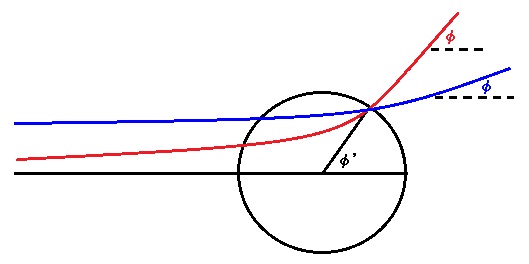
この様な図を思い浮かべて、分かったと感じ、その後は考えませんでしたが、TEC-0-1-37-15,16を執筆した時に、計算ミスに気付いた様です。
2015年11月にこの補足説明を書き始めた時には、その事を忘れていて、計算ミスに気付く前の考えに逆戻りしていました。
φ → 0 で b → ∞ ならば全断面積が無限大に成る事は、
2π∫0π dφ (sinφ)σ = 2π∫0π dφb|db|/|dφ|
= -2π∫0π dφb(db/dφ) ∵ db/dφ < 0
= -∫0π dφ(d/dφ)(πb2)
= -[π×(φ=πに成るbの値)2 - π×(φ=0に成るbの値)2]
= π×(φ=0に成るbの値)2 ∵(φ=πに成るbの値) = 0
という風に考えれば、具体的な計算を抜きしにして、一般論のまま分かります。
さらに、この考え方は、φを使おうが上図のφ'を使おうが変わらない事に、2015年11月09日に気付きました。
つまり、2π(sinφ)dφが斥力の中心から見た正しい微小立体角を表していようがいまいが、微分断面積の定義において 2π(sinφ) で割り、積分において 2π(sinφ) を掛けるのだから、そんな事は結果には影響しない、という事です。2015.11.06,07,08,09,30
TEC-0-5-114
【SEOテキスト】03.10.20宇田雄一dφ/dh=-2 -1/2 2KhZ/m/[(Z/m)2+Kh2]3/2・1/-sinθ0=-2KhZ/m/[(Z/m)2+Kh2]3/2・√ (Z/m)2+Kh2 / Kh2=-2Z/m √K 1/ (Z/m)2+Kh2,σ=b/sinφ|db/dφ|=1/2 m/Z (Z/m)2+Kh2 /K・b/sinφ,sinφ=sin(π-2θ0)=sin 2θ0=2(sinθ0)cosθ0=2√K h/√ (Z/m)2+Kh2・Z/m/√ (Z/m)2+Kh2=2Z/m √K h/ (Z/m)2+Kh2∴σ=[1/2・m/Z・(Z/m)2+Kh2 /K]2=(b/sinφ)2,CAN-1-1-13-28,29,TEC-0-1-36-4〜25衝突径数をもっと簡単に求めるためには、r2θ=h,r2=-h2/r2-2(Z/m)/r+Kを用いてvb=r2θ=h,v2=K∴b=h/√Kと考えれば良い事がCAN-1-1-14-1〜8の図より分かる。ただしvはt→-∞における質点の速さを表すものとする。CAN-1-1-13-26〜14-8,bは、質点の軌道の漸近線と、それに平行で原点を通る直線の、距離を表す。破線は漸近線に平行で原点を通る直線を表す。2πb|db|は入射微小断面積を表し、2π(sinφ)|dφ|はそれに対応する出射微小立体角を表す。σは単位出射立体角あたりの入射断面積を意味する。