
次のページ
前のページ
目次
【補足説明欄】
1〜16行目の内容は、TEC-0-1-30-18〜21の数直線で定義されている場合IV[Z = -mh2/(2a)]についてです。2015.02.26
2行目の式の成立根拠は、TEC-0-1-30-18〜21の数直線による場合IVの定義
Z = -mh2/(2a)
です。
「(19)より、」という文言は、TEC-0-1-29-22〜28の式がTEC-0-1-34-2の式の成立根拠だ、と主張するものですが、これは誤りです。2015.02.26
TEC-0-1-31のIVのグラフから、IVでは、1/r の値は
t → -∞ で 1/r → +0
から単調増加した後で、1/r = -2Z/(mh2) で折り返し、その後は
t → +∞ で 1/r → +0
まで単調減少する事が分かります。
1/r = 0 に達する事は出来ないので、1/r = 0 で折り返す事は有りません。
従って、r = -mh2/(2Z) に成る時刻をt軸の原点とし、
-mh2/(2Z) = a ∵TEC-0-1-34-2
である事に気を付けると、r と t の関係はTEC-0-1-34-10〜15の左のグラフの様に成る事が分かります。
TEC-0-1-32-4,5から、
du/dt < 0(dr/dt > 0) ならば dθ/du < 0
du/dt > 0(dr/dt < 0) ならば dθ/du > 0
だと分かるので、TEC-0-1-34-10〜15の左のグラフを参照すれば、u とθの関係がTEC-0-1-34-10〜15の右のグラフの様に成る事が分かります。
ただし、u = 1/a に成るθの値をθ軸の原点としました。
u → +0 でθ→±πである事は、ここまでの考察だけからでは、分かりません。
TEC-0-1-32-24〜29の右のグラフに記入されている様な時間経過の向きを表す矢印、を記入し忘れています。
TEC-0-1-34-10〜15の左右両方のグラフの詳細が決まれば、t → r → u →θという風に関数関係を繋げて行く事によって、r とθは t のどんな関数か、が決まります。
TEC-0-1-34-10〜15の左のグラフの詳細は、TEC-0-1-34-3,4の条件によって決まります。
TEC-0-1-34-10〜15の右のグラフの詳細は、TEC-0-1-34-7,8の左の等号で表されている条件によって決まります。2015.02.26;2015.07.30
3,4行目の等号の成立は、TEC-0-1-29-15,16の式とK=0である事(TEC-0-1-30-27)を基にして、次の様に考えれば、分かります。
t ≦ 0 の場合には、t の値が t から 0 まで増加する間に、r の値は r から a まで減少します。
従って、0 - t = ∫ra dr dt/dr = ∫ar dr (-dt/dr) = ∫ar dr |dt/dr| です。(∵ dt/dr < 0)
t ≧ 0 の場合には、t の値が 0 から t まで増加する間に、r の値は a から r まで増加します。
従って、t - 0 = ∫ar dr dt/dr = ∫ar dr |dt/dr| です。(∵ dt/dr > 0)
これら両方をまとめると、
|t| = ∫ar dr |dt/dr|
という風に書けます。2015.02.26;2015.07.26
5,6行目の等号の成立根拠は、以下の積分計算です。
まず不定積分を計算します。
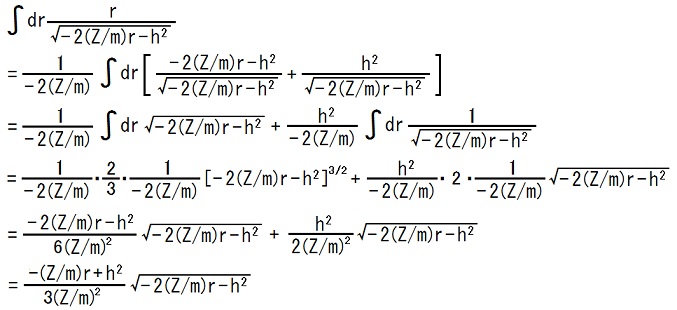
積分定数は省略しました。
不定積分の結果を使って、定積分は、次の様に計算できます。
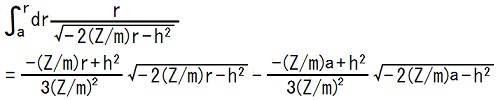
ところが、
-2(Z/m)a - h2 = 0 ∵TEC-0-1-34-2
だから、右辺第2項はゼロです。2015.02.26;2015.07.26
7,8行目の左の等号の成立は、TEC-0-1-32-4,5の式とK=0である事(TEC-0-1-30-27)を基にして、次の様に考えれば、分かります。
θ ≦ 0 の場合には、u の値が u から 1/a まで増加する間に、θの値はθから 0 まで増加します。
従って、0 - θ = ∫u1/a du dθ/du = ∫u1/a du |dθ/du| です。(∵ dθ/du > 0)
θ ≧ 0 の場合には、u の値が 1/a から u まで減少する間に、θの値は 0 からθまで増加します。
従って、θ - 0 = ∫1/au du dθ/du = ∫u1/a du (-dθ/du) = ∫u1/a du |dθ/du| です。(∵ dθ/du < 0)
これら両方をまとめると、
|θ| = ∫u1/a du |dθ/du|
という風に書けます。2015.02.26;2015.07.26,30
7,8行目の cos-1 の値としては、TEC-0-1-35-15の条件を満たす実数を、用います。2015.02.26
7,8行目の最右辺中の Z/mh2 は Z/(mh2) です。2015.07.30
7,8行目の右の等号の成立根拠は、TEC-0-1-32-16,17の等号の成立根拠として説明されている不定積分の結果にK = 0 を代入して得られる式です。
h > 0 である事は、TEC-0-1-29-9に書かれています。
Kh2 + (Z/m)2 > 0 である事は、TEC-0-1-30-27に、書かれています。
この不定積分を使って定積分を計算すると、
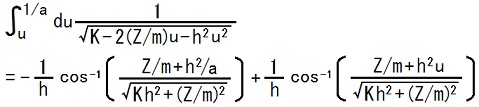
ここで、
Z/m + h2/a = -Z/m ∵TEC-0-1-34-2
√[Kh2 + (Z/m)2] = √[(Z/m)2] = √[(-Z/m)2] = -Z/m ∵ K = 0, -Z/m > 0 ∵ Z = -mh2/(2a)[TEC-0-1-30-18〜21]
および cos-1(1) = 0 である事を使うと、右辺の第1項はゼロだ、と分かり、第2項内の根号を外す事も出来ます。
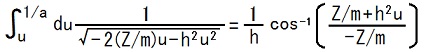
この結果に h を掛ける事によって、TEC-0-1-34-7,8行目の式を得る事が出来ます。2015.02.26;2015.07.26,30
10〜15行目の右のグラフに書かれている様に、u → +0 でθ→±πである事は、7,8行目の式で、極限 u → +0 を考え、ξ→ -1 で cos-1(ξ) → π である事を使うと、分かります。2015.02.26;2015.07.30
7,8行目の式と、IVではZ<0である事(TEC-0-1-30-18〜21)を使うと、
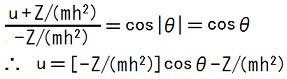
ここでTEC-0-1-32-1,2を使うと、
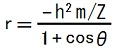
これは、半直弦の長さが-h2m/Zである放物線の方程式に一致しています。2015.02.26;2015.07.30
---
---
TEC-0-1-34-17〜TEC-0-1-35-14の内容は、TEC-0-1-30-18〜21の数直線で定義されている場合V[-mh2/(2a) < Z < 0]と場合VII(Z > 0)についてです。2015.02.26
TEC-0-1-31のV,VIIのグラフから、V,VIIでは、1/r の値は
t → -∞ で 1/r → +0
から単調増加した後で、1/r = 1/r1 で折り返し、その後は
t → +∞ で 1/r → +0
まで単調減少する事が分かります。
1/r = 0 に達する事は出来ないので、1/r = 0 で折り返す事は有りません。
従って、r = r1 に成る時刻をt軸の原点とし、
r1 = a ∵TEC-0-1-30-28,30
である事に気を付けると、r と t の関係はTEC-0-1-35-1〜7のグラフの様に成る事が分かります。
TEC-0-1-32-4,5から、
du/dt < 0(dr/dt > 0) ならば dθ/du < 0
du/dt > 0(dr/dt < 0) ならば dθ/du > 0
だと分かるので、TEC-0-1-35-1〜7のグラフを参照すれば、u とθの関係がTEC-0-1-35-8〜14のグラフの様に成る事が分かります。
ただし、u = 1/a に成るθの値をθ軸の原点としました。
TEC-0-1-35-1〜14のグラフの詳細が決まれば、t → r → u →θという風に関数関係を繋げて行く事によって、r とθは t のどんな関数か、が決まります。
TEC-0-1-35-1〜7のグラフの詳細は、TEC-0-1-34-18,19の条件によって決まります。
TEC-0-1-35-8〜14のグラフの詳細は、TEC-0-1-34-24,25の条件によって決まります。2015.02.26;2015.07.30
18,19行目の等号の成立は、TEC-0-1-29-15,16の式を基にして、次の様に考えれば、分かります。
t ≦ 0 の場合には、t の値が t から 0 まで増加する間に、r の値は r から a まで減少します。
従って、0 - t = ∫ra dr dt/dr = ∫ar dr (-dt/dr) = ∫ar dr |dt/dr| です。(∵ dt/dr < 0)
t ≧ 0 の場合には、t の値が 0 から t まで増加する間に、r の値は a から r まで増加します。
従って、t - 0 = ∫ar dr dt/dr = ∫ar dr |dt/dr| です。(∵ dt/dr > 0)
これら両方をまとめると、
|t| = ∫ar dr |dt/dr|
という風に書けます。2015.02.26
22,23行目の cosh-1 の値としては、TEC-0-1-35-15の条件を満たす実数を、用います。2015.02.26
20,21行目の等号の成立根拠は、以下の積分計算です。
まず不定積分は、TEC-0-1-32-10,11行目の等号の成立根拠として説明されている積分計算の赤枠で囲まれた部分を、以下の積分計算に置き換えます。

すると、TEC-0-1-32-10,11行目の等号の成立根拠として説明されている不定積分は、次の式に書き換えられます。
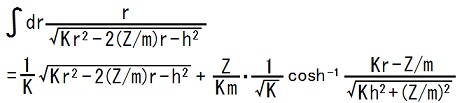
積分定数は省略しました。
K > 0 である事と、 Kh2 + (Z/m)2 > 0 である事は、TEC-0-1-30-28,30に書かれています。
coshψの置き方は、
Kr - Z/m ≧ √[(Z/m)2 + Kh2]
である事に依拠していますが、これは、
Ka - Z/m = √[(Z/m)2 + Kh2] ∵ r1 = a(TEC-0-1-30-28,30); TEC-0-1-30-4,5
r ≧ a ∵ r1 = a(TEC-0-1-30-28,30); r ≧ r1(TEC-0-1-31-V,VII)
によって保証されています。
不定積分の結果を使って、定積分は、次の様に計算できます。
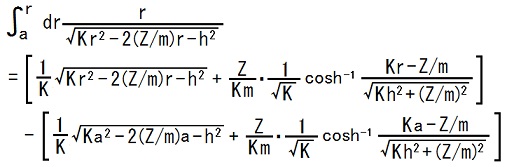
ところが、
a > 0(TEC-0-1-29-9)とTEC-0-1-29-13,14の式と、r=r1でdr/dt=0に成る事(TEC-0-1-31-V,VII)と、r1 = a(TEC-0-1-30-28,30)から
Ka2 - 2(Z/m)a - h2 = 0
が言える(TEC-0-1-29-13,14の式に r = a, dr/dt = 0 を代入すれば分かる)ので、右辺の第2角括弧[ ]内の第1項はゼロだ、と分かります。さらに、
r1 = a(TEC-0-1-30-28,30)とTEC-0-1-30-4,5の式から、
Ka - Z/m = √[(Z/m)2 + Kh2]
が言え、また cosh-1(1) = 0 だから、右辺の第2角括弧[ ]内の第2項もゼロだ、と分かります。2015.02.26;2015.07.30
24,25行目の左の等号の成立は、TEC-0-1-32-4,5の式を基にして、次の様に考えれば、分かります。
θ ≦ 0 の場合には、u の値が u から 1/a まで増加する間に、θの値はθから 0 まで増加します。
従って、0 - θ = ∫u1/a du dθ/du = ∫u1/a du |dθ/du| です。(∵ dθ/du > 0)
θ ≧ 0 の場合には、u の値が 1/a から u まで減少する間に、θの値は 0 からθまで増加します。
従って、θ - 0 = ∫1/au du dθ/du = ∫u1/a du (-dθ/du) = ∫u1/a du |dθ/du| です。(∵ dθ/du < 0)
これら両方をまとめると、
|θ| = ∫u1/a du |dθ/du|
という風に書けます。2015.02.26;2015.07.30
26〜29行目の cos-1 の値としては、TEC-0-1-35-15の条件を満たす実数を、用います。2015.02.26
26,27行目の等号の成立根拠は、TEC-0-1-33-14,15の等号の成立根拠と同様です。
Kh2 + (Z/m)2 > 0 である事は、TEC-0-1-30-28,30に、書かれています。2015.02.26;2015.07.26
28,29行目のθ0 は、u → +0, θ→±θ0 の時に24,25行目の等号が成立する様に選ばれた物です。
幸いな事に、条件は2つ(θ→+θ0 に対する条件とθ→-θ0 に対する条件)あるのに、その様なθ0 が存在しています。
この事が、TEC-0-1-35-8〜14で左右対称なグラフを仮定した事を正当化します。2015.02.26;2015.07.26
24〜27行目の式と、Vでは Z < 0 である事(TEC-0-1-30-18〜21)と、 m>0である事(CAN-1-1-4の質量に対する補足説明)を、使うと、
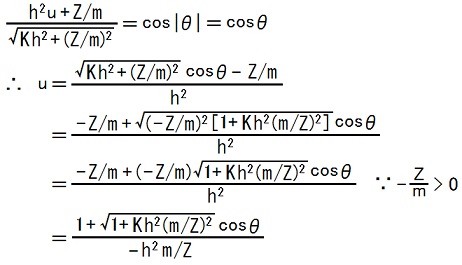
ここでTEC-0-1-32-1,2を使うと、
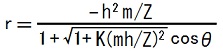
これは、半直弦の長さが-h2m/Zである双曲線の方程式に一致しています。
Vでは K > 0 である事(TEC-0-1-30-28)と、
m≠0 である事(CAN-1-1-4の質量に対する補足説明)と、
h≠0 である事(TEC-0-1-29-9)と、
Z≠0 である事(TEC-0-1-30-15,16に対する補足説明)から、
√[1+K(mh/Z)2] > 1
だと分かります。2015.02.26;2015.04.02;2015.07.26,30
24〜27行目の式と、VIIでは Z > 0 である事(TEC-0-1-30-18〜21)と、m>0である事(CAN-1-1-4の質量に対する補足説明)を、使うと、
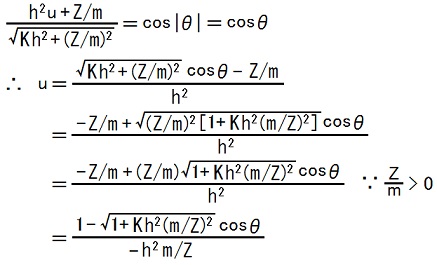
ここでTEC-0-1-32-1,2を使うと、
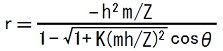
これは、半直弦の長さが-h2m/Zである双曲線の方程式に一致しています。
VIIでは K > 0 である事(TEC-0-1-30-30)と、
m≠0 である事(CAN-1-1-4の質量に対する補足説明)と、
h≠0 である事(TEC-0-1-29-9)と、
Z≠0 である事(TEC-0-1-30-15,16に対する補足説明)から、
√[1+K(mh/Z)2] > 1
だと分かります。2015.02.26;2015.04.02;2015.07.26,30
【SEOテキスト】03.10.20宇田雄一,逆2乗中心力問題IV,(19)より、-2Z/mh2=1/a,|t|=∫r,a rdr/√ -2(Z/m)r-h2=m2/3Z2(-Z/m r+h2)√ -2Z/m r-h2,|θ|=∫1/a,u hdu/√ -2(Z/m)u-h2u2=cos-1(u+Z/mh2 / -Z/mh2),r,a,O,t,u,1/a,-π,O,π,θ,V,VII,|t|=∫r,a rdr/√ Kr2-2(Z/m)r-h2=1/K √ Kr2-2(Z/m)r-h2 +Z/mK√K cosh-1[Kr-Z/m /√ (Z/m)2+Kh2],|θ|=∫1/a,u hdu/√ K-2(Z/m)u-h2u2=cos-1[h2u+Z/m / (Z/m)2+Kh2],θ0≡cos-1[Z/m / (Z/m)2+Kh2]