次のページ
前のページ
目次
【補足説明欄】
4,5行目の式の成立根拠は、1,2行目の式とTEC-0-1-29-8,15,16の式です。
∵TEC-0-1-32-1,2
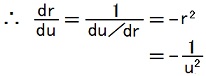∵TEC-0-1-32-1,2
= (-1/u2)×(TEC-0-1-29-15,16の式)×(TEC-0-1-29-8の式÷r2)
= -(TEC-0-1-29-15,16の式)×(TEC-0-1-29-8の式) ∵ (1/u2)(1/r2) = 1 ∵TEC-0-1-32-1,2
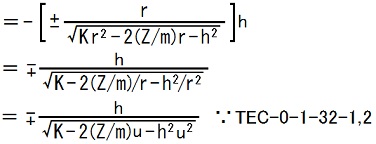
複号はTEC-0-1-29-15,16の式に由来するので、dr/dt > 0(dt/dr > 0)ならば上の符号が、dr/dt < 0(dt/dr < 0)ならば下の符号が、選択されます。
TEC-0-1-29-15,16の式とTEC-0-1-32-4,5の式では複号の順序が逆である事、に気を付けて下さい。2014.12.18;2015.02.17;2015.07.23
TEC-0-1-32-6〜TEC-0-1-35-15では、TEC-0-1-31のグラフと、TEC-0-1-29-15,16の式と、TEC-0-1-32-4,5の式を基にして、球面振り子(CAN-1-1-12-1〜11)についてTEC-0-1-23の補足説明欄の赤枠で囲まれている部分に書かれているの、と同様の考え方に従います。
1/r の値は、TEC-0-1-31のグラフから定まる|dr/dt|で r の値が変化する様に、1/r 軸上を運動します。
|dr/dt| = 0 ならば (d/dt)(1/r) = 0 なので、そこでは 1/r の値は(1/r = 0 は別ですが)運動の向きを変えて折り返します。2014.12.18,19;2015.02.17
TEC-0-1-32-6〜30の内容は、TEC-0-1-30-18〜21の数直線で定義されている場合I(Z < -mh2/a)についてです。2015.02.22
TEC-0-1-31-I,IIIのグラフから、Iでは 1/r の値は 1/r0 と 1/r1 の間を往復する事が分かります。
今考えているのは I の場合だから、TEC-0-1-30-24から r0 = a > r1 だと分かります。
従って、r = a に成る時刻の1つをt軸の原点とすると、r と t の関係は、TEC-0-1-32-24〜29の左のグラフの様に、成ります。
TEC-0-1-32-4,5から、
du/dt < 0(dr/dt > 0) ならば dθ/du < 0
du/dt > 0(dr/dt < 0) ならば dθ/du > 0
だと分かるので、TEC-0-1-32-24〜29の左のグラフを参照すれば、u とθの関係がTEC-0-1-32-24〜29の右のグラフの様に成る事が分かります。
ただし、u = 1/a に成るθの値の1つをθ軸の原点としました。
グラフ中の矢印は、時間経過の向きを表しています。
TEC-0-1-32-24〜29の左右両方のグラフの詳細が決まれば、t → r → u →θという風に関数関係を繋げて行く事によって、r とθは t のどんな関数か、が決まります。
tとθの対応には、左のグラフのどの1周期と右のグラフのどの1周期を対応させるか、に相当する任意性が存在しますが、左のグラフのどの1周期と右のグラフのどの1周期を対応させるかを変更する事は、θ軸の原点を変更する事と等価だから、この任意性は同一の物理的内容に対する数式表現の任意性に過ぎず、t = 0 でθ= 0 だ、という条件によって特定の対応を選択しても、物理的内容は減りません。
だから、t = 0 でθ= 0 だ、としておきます。
TEC-0-1-32-24〜29の左のグラフの詳細は、TEC-0-1-32-7〜9の条件によって決まります。
TEC-0-1-32-24〜29の右のグラフの詳細は、TEC-0-1-32-7,14,15の条件によって決まります。2014.12.18,19,20;2015.02.17,19,22
7行目の条件 0 ≦ |t - 2nt0| ≦ t0 は、t と 2nt0 の間隔が t0 以下だ、という条件だから、
2nt0 - t0 ≦ t ≦ 2nt0 + t0
つまり、
(2n - 1)t0 ≦ t ≦ (2n + 1)t0
という風に、書き直せます。2014.12.18,19
8,9行目の等号の成立は、TEC-0-1-29-15,16の式を基にして、TEC-0-1-23-18〜23(補足説明も)と同様に考えれば、分かります。
(2n - 1)t0 ≦ t ≦ 2nt0 の場合には、t の値が t から 2nt0 まで増加する間に、r の値は r から a まで増加します。
従って、2nt0 - t = ∫ra dr dt/dr = ∫ra dr |dt/dr| です。(∵ dt/dr > 0)
2nt0 ≦ t ≦ (2n + 1)t0 の場合には、t の値が 2nt0 から t まで増加する間に、r の値は a から r まで減少します。
従って、t - 2nt0 = ∫ar dr dt/dr = ∫ra dr (-dt/dr) = ∫ra dr |dt/dr| です。(∵ dt/dr < 0)
これら両方をまとめると、
|t - 2nt0| = ∫ra dr |dt/dr|
という風に書けます。2014.12.18;2015.02.19
12,13,16,17行目の cos-1 の値としては、TEC-0-1-35-15の条件を満たす実数を、用います。2014.12.25
10,11行目の等号の成立根拠は、以下の積分計算です。
まず、不定積分を計算します。
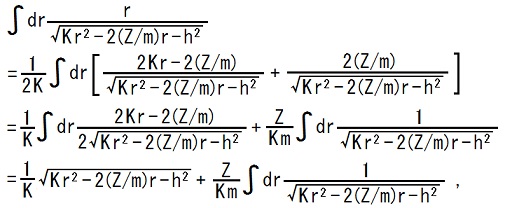
この式の第2項の積分は、以下の赤枠内で計算されています。
 |
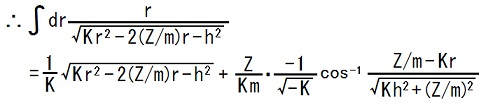
積分定数は省略しました。
-K > 0 である事と Kh2 + (Z/m)2 > 0 である事は、TEC-0-1-30-24に、書かれています。
高校数学ですが、念のために説明しておきます。
まず最初に、分母の根号の中身が r の2次式で、分子が r の1次式である事に着目します。
これを見て、分母の根号の中身の微分が分子に一致する様な形を捻出できる、という風に判断します。
その捻出で派生してしまった分子が定数の積分については、根号の中を
(正の定数) - (r の関数)2
とか
(正の定数) + (ｒ の関数)2
という形に変形する事を目指します。
(正の定数) - (r の関数)2
という形に変形できれば、(r の関数)部分を
(正の定数)1/2cosψ
と置く事によって、根号の中を
(正の定数)×(sinψ)2
の形にして、根号を外す事が出来るし、
(正の定数) + (r の関数)2
という形に変形できれば、(r の関数)部分を
(正の定数)1/2tanψ
と置く事によって、根号の中を
(正の定数)×(1/cosψ)2
の形にして、根号を外す事が出来ます。
私の場合、見通しはそこまでで、根号を外した後も上手く行くか否かは、事前には判断しません。
ここまでは、不定積分の計算について、です。
不定積分の結果を使って、定積分は、次の様に計算できます。
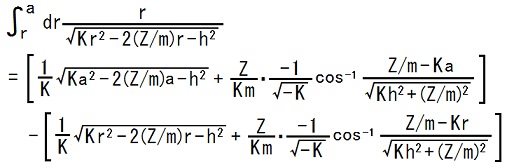
ところが、
a > 0(TEC-0-1-29-9)とTEC-0-1-29-13,14の式と、r=r0でdr/dt=0に成る事(TEC-0-1-31-I,III)と、r0 = a(TEC-0-1-30-24)から、
Ka2 - 2(Z/m)a - h2 = 0
が言える(TEC-0-1-29-13,14の式に r = a, dr/dt = 0 を代入すれば分かる)ので、右辺の第1角括弧[ ]内の第1項はゼロだ、と分かります。さらに、
r0 = a(TEC-0-1-30-24)とTEC-0-1-30-2,3の式から、
Z/m - Ka = √[(Z/m)2 + Kh2]
が言え、また cos-1(1) = 0 だから、右辺の第1角括弧[ ]内の第2項もゼロだ、と分かります。2014.12.25;2015.02.04,07,09,10,17,19;2015.07.22,30
14,15行目の等号の成立は、TEC-0-1-32-4,5の式を基にして、TEC-0-1-23-18〜23(補足説明も)と同様に考えれば、分かります。
(2n - 1)θ0 ≦ θ ≦ 2nθ0 の場合には、u の値が u から 1/a まで減少する間に、θの値はθから 2nθ0 まで増加します。
従って、2nθ0 - θ = ∫u1/a du dθ/du = ∫1/au du (-dθ/du) = ∫1/au du |dθ/du| です。(∵ dθ/du < 0)
2nθ0 ≦ θ ≦ (2n + 1)θ0 の場合には、u の値が 1/a から u まで増加する間に、θの値は 2nθ0 からθまで増加します。
従って、θ - 2nθ0 = ∫1/au du dθ/du = ∫1/au du |dθ/du| です。(∵ dθ/du > 0)
これら両方をまとめると、
|θ - 2nθ0| = ∫1/au du |dθ/du|
という風に書けます。2014.12.19;2015.02.19,22,23
16,17行目の等号の成立根拠は、以下の積分計算です。
まず、不定積分を計算します。
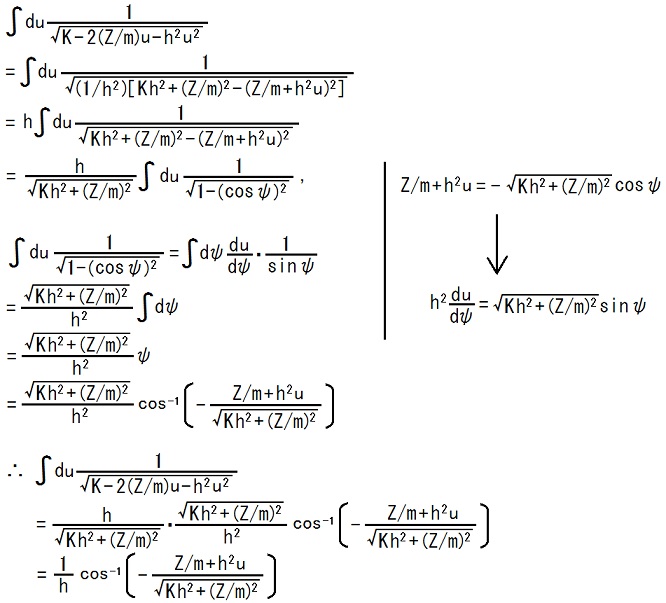
積分定数は省略しました。
上の赤枠で囲まれた積分において、Kを-h2に、-h2をKに、rをuに書き換えた場合と、同様ですが、cosψの置き方の符号が違います。
h > 0 である事は、TEC-0-1-29-9に書かれています。
Kh2 + (Z/m)2 > 0 である事は、TEC-0-1-30-24に、書かれています。
ここまでは、不定積分の計算について、です。
不定積分の結果を使って、定積分は、次の様に計算できます。
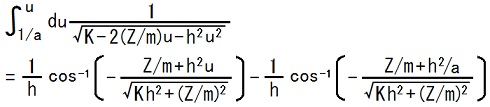
ところが、
Z < -mh2/a ∵TEC-0-1-30-18〜21
∴ Z/m + h2/a < 0
これとTEC-0-1-30-7の式から、
Z/m + h2/a = -√[Kh2 + (Z/m)2]
だと分かり、また cos-1(1) = 0 だから、右辺の第2項はゼロだ、と分かります。
cosψの置き方の符号は、こう成る様に決めました。
赤枠内の計算結果を利用する事も出来ます。
赤枠内の計算結果において、Kを-h2に、-h2をKに、rをuに書き換えれば、
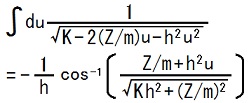
だと分かります。
この不定積分を使えば、定積分は、次の様に計算できます。
これは、cosψのもう一つの置き方を採用した場合と、ちゃんと同じに成っています。
この結果に h を掛ける事によって、TEC-0-1-32-16,17行目の式を得る事が出来ます。2015.02.04,07,08,10;2015.02.17,19,23;2015.07.25,26,30
19,20行目の t0 は、r = r1, t = (2n±1)t0 の時に8,9行目の等号が成立する様に選ばれた物です。
幸いな事に、全ての n に渡ってそう成る様な単一の t0 が存在しています。
この事が、TEC-0-1-32-24〜29の左のグラフで周期関数を仮定した事を正当化します。2014.12.19,20;2015.07.22
21,22行目のθ0は、 u = 1/r1, θ = (2n±1)θ0 の時に14,15行目の等号が成立する様に選ばれた物です。
幸いな事に、全ての n に渡ってそう成る様な単一のθ0が存在しています。
この事が、TEC-0-1-32-24〜29の右のグラフで周期関数を仮定した事を正当化します。2014.12.19,20;2015.07.22
19,20行目の右の等号の成立根拠は、10,11行目の等号の成立と、r = r1でdr/dt = 0に成る事(TEC-0-1-31-I,III)と、TEC-0-1-29-13,14の式と、TEC-0-1-30-4,5の右の等号です。
r = r1でdr/dt = 0に成る事と、TEC-0-1-29-13,14の式から、
Kr12 - 2(Z/m)r1 - h2 = 0
だと分かります。
従って、TEC-0-1-32-10,11の項に r = r1 を代入すると、ゼロに成ります。
TEC-0-1-30-4,5の右の等号から、
-Kr1 + Z/m = -√[(Z/m)2 + Kh2]
だと分かるので、TEC-0-1-32-12,13の項に r = r1 を代入すると、
という風に成ります。2015.02.15,19;2015.07.30
21,22行目の右の等号の成立根拠は、16,17行目の等号の成立と、TEC-0-1-30-4,5の右の等号の成立です。
TEC-0-1-30-4,5の右の等号の成立を根拠にして、中学数学で習う「分母の有理化」の技法を真似れば、
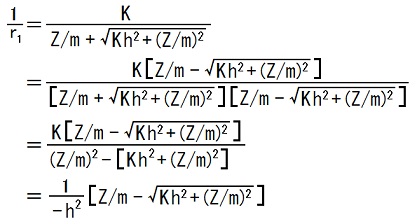
という風に計算できます。
この計算結果は、偶然の幸運ではなく、TEC-0-1-29-13,14の式を dr/dt=0 の場合に、1/r についての2次方程式と見て、これに解の公式を適用すれば、こう成るべくしてこう成った物だと分かります。
この計算結果から、
h2(1/r1) + Z/m = √[(Z/m)2 + Kh2]
だと分かります。
従って、TEC-0-1-32-16,17の辺に、u = 1/r1 を代入すると、
cos-1(-1) = π
という風に成ります。
u がθの周期関数であり、その周期が 2θ0 = 2π である事から、軌道は閉じている、と分かります。2015.02.15,22;2015.07.22,23,25
14〜17行目の式と、θ0 = πである事(21,22行目)と、IではZ<0である事(TEC-0-1-30-18〜21)と、m>0である事(CAN-1-1-4の質量に対する補足説明)を使うと、
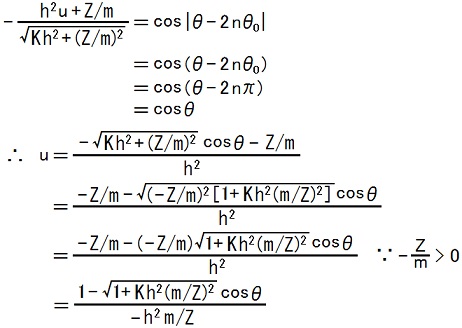
ここでTEC-0-1-32-1,2を使うと、
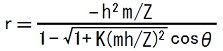
これは、半直弦の長さが-h2m/Zで、離心率が√[1+K(mh/Z)2]の楕円の方程式に一致しています。
Iでは K < 0 である事(TEC-0-1-30-24)と、
m≠0 である事(CAN-1-1-4の質量に対する補足説明)と、
h≠0 である事(TEC-0-1-29-9)と、
Z≠0 である事(TEC-0-1-30-15,16に対する補足説明)から、
√[1+K(mh/Z)2] < 1
だと分かります。
1+K(mh/Z)2 ≧ 0
である事は、TEC-0-1-30-7の式によって保証されています。
(Z/m)2 + Kh2 ≧ 0 ∵TEC-0-1-30-7
(m/Z)2 ≧ 0
だから、
1+K(mh/Z)2 = (m/Z)2[(Z/m)2 + Kh2] ≧ 0
だと分かります。2015.02.15,22,23,25;2015.04.02;2015.07.25,26,30
【SEOテキスト】03.10.19宇田雄一,逆2乗中心力問題u=1/r・・・・・・・・・(27)とおくと、(13)(14)より、dθ/du=-+h/√K-2(Z/m)u-h2u2,(-)r>0のとき(+)r<0のとき}(28),I,0≦|t-2nt0|≦t0ならば|t-2nt0|=∫a,r rdr/√Kr2-2(Z/m)r-h2=1/-K √Kr2-2(Z/m)r-h2+Z/mK√-K cos-1[-Kr+Z/m /√ (Z/m)2+Kh2],|θ-2nθ0|=∫u,1/a hdu/√ K-2(Z/m)u-h2u2=cos-1[- h2u+Z/m /√ (Z/m)2+Kh2]ただしt0≡∫a,r1 rdr/√ Kr2-2(Z/m)r-h2=πZ/ mK√-K,θ0≡∫1/r1,1/a hdu/√ K-2(Z/m)u-h2u2=π,r,a,r1,-t0,O,t0,t,u,1/r1,1/a,-θ0,θ0,θ