
次のページ
前のページ
目次
CAN-1-1-13
【補足説明欄】
7,8行目の式の根拠は、CAN-1-1-13-23の式です。2014.12.12
9行目の条件は、CAN-1-1-13-24の条件です。2014.12.12
11,12行目の式の成立は、
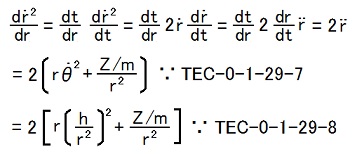
という風に考えれば、分かります。2014.12.12;2015.07.18
13,14行目の式は、11,12行目の式を不定積分する事によって得られます。
Kは積分定数です。2014.12.12;2015.07.19
15,16行目の式は、
という風に考えれば、分かります。2014.12.12;2015.07.19
18,19行目の式は、13,14行目の式が t についての恒等式である事に着目して、t = 0 での値を考える事によって、分かります。
13,14行目の式に、r = a(9行目) と dr/dt = 0(9行目) を代入すると、
これをKについて代数的に解けば、18,19行目の式が得られます。2014.12.12;2015.07.19
21行目に書かれている条件 m > 0 は、CAN-1-1-4の補足説明欄にも書かれています。2015.07.19
22〜28行目の場合分けでは、a, h を固定し Z を変化させて調べていますが、変数の意味を考えると本来は、与えられた m, Z に対して a, h の値を色々と変えて調べるのが正しいはずです。
つまり、私は a, h を定数として、Z を変数として扱っていますが、本当は m, Z が定数であり a, h が変数のはずだ、という疑問が考えられます。
この点については、変数か定数かという区分けは図形に引かれた補助線の様な物に過ぎず対象(式)そのものの属性ではない、という理解の仕方を私はしています。
たとえば、y = ax + b という御馴染みの式においては、a, b が定数で x, y が変数だ、という風に考えるのが普通ですが、言ってみれば、文字で書かれている以上は a, b も変数なんです。
22〜28行目の式では、a, h を定数、Z を変数と見なす補助線の引き方をしていますが、これは漏れを無くす為の工夫であり、その正当性は、図形の問題で補助線の引き方は任意であり補助線の引き方を変えても結論は変わらない、のと同様です。
23〜28行目の式を、Z の値を与えた時の a, h に対する条件、と見る事も出来ます。
そう見た時には、Z を定数、a, h を変数と見ている事に成ります。
定数か変数かについては、式が ∀a; ∀x; ・・・ という風に書かれていれば a が定数で x が変数、式が ∀x; ∀a; ・・・ という風に書かれていれば x が定数で a が変数、という風に判別でき、両者が論理的に同値ならば区別は客観的ではない、と言えます。2014.12.14;2015.07.19
【SEOテキスト】宇田雄一03.10.18逆2乗中心力問題CAN-1-1-13-20〜25以下において資料(宇田の昔のノート)からの引用の都合上、式番号が変ですが気にしないで下さい。r-rθ2=(Z/m)/r2・・・・・・・・・・(11)r2θ=h・・・・・・・・・・(13)t=0でr=a>0,θ=0,r=0,θ=h/a2>0・・・・・・・(17),(11)(13)より、dr2/dr=2h2/r3+2Z/m・1/r2∴r2=-h2/r2-2Z/m・1/r+K・・・・・・・・・・(14)'∴dt/dr=±r/√Kr2-2(Z/m)r-h2・・・・・・・・・・・(14),(17)と(14)'より、K=h2/a2+2Z/ma・・・・・・・・・・(16),(17)よりh>0・・・・・・・・・・(18)m>0は当然前提として、(17)(16)より、Z>0⇒K>0,-mh2/2a<Z<0⇒K>0,Z=-mh2/2a⇒K=0,Z<-mh2/2a⇒K<0}・・・・・・・・(19)