
次のページ
前のページ
目次
CAN-1-1-12
TEC-0-1-56
COM-1-10
【補足説明欄】
2,3行目の左の等号の成立は、
(d/dt)[(sinθ)2dφ/dt]
= {(d/dt)[(sinθ)2]}dφ/dt + (sinθ)2d2φ/dt2
= [(dθ/dt)(ds/dθ)(d/ds)s2]dφ/dt + (sinθ)2d2φ/dt2 (s ≡ sinθ)
= (dθ/dt)(cosθ)2s dφ/dt + (sinθ)2d2φ/dt2
という風に考えれば、分かります。2014.11.13
6行目に書かれている代入では、
dφ/dt = h/(sinθ)2
を代入します。2014.11.13
7行目の式を得るために、代入後両辺をmで割りました。2014.11.13
9,10行目の式の成立根拠は、以下の3つです。
2a(dθ/dt)(d2θ/dt2) = a(d/dt)(dθ/dt)2・・・(1)
-2ah2(dθ/dt)(cosθ)(sinθ)-3 = ah2(d/dt)(sinθ)-2・・・(2)
2g(dθ/dt)sinθ = -2g(d/dt)cosθ・・・(3)
(1)の成立は、w ≡ dθ/dt と書いて、
(d/dt)w2 = (dw/dt)(d/dw)w2 = 2w dw/dt
という風に考える事によって、分かります。
(2)の成立は、s ≡ sinθ と書いて、
(d/dt)(sinθ)-2
= (dθ/dt)(ds/dθ)(d/ds)s-2
= (dθ/dt)(cosθ)(-2s-3)
という風に考える事によって、分かります。
(3)の成立は、u ≡ cosθ と書いて、
du/dt = (dθ/dt)(du/dθ) = (dθ/dt)(- sinθ)
と考える事によって、分かります。2014.11.13,22
11,12行目の式は、9,10行目の式の両辺をtで不定積分する事によって得られた式です。
9,10行目の式から、
(d/dt)[a(dθ/dt)2 + ah2(sinθ)-2 + 2g cosθ] = 0
だと分かります。
この事と、微分して0に成るのは定数だけである事から、
a(dθ/dt)2 + ah2(sinθ)-2 + 2g cosθ = E'(定数)
と書けます。
この式を (dθ/dt)2 について解くと、
(dθ/dt)2 = E'/a - h2(sinθ)-2 - 2(g/a)cosθ
この式の E'/a を E と書く事にした物が、11,12行目の式です。2014.11.13,22
11〜17行目の右端に描かれているグラフは、11,12行目の式に対する物です。
グラフの概形の根拠は、11,12行目の式の右辺を u ≡ cosθ の関数とみなす事によって、分かります。
(sinθ)2 = 1 - u2 だから、
(dθ/dt)2 = F(u) ≡ E - h2/(1 - u2) - 2(g/a)u
(d/du)F(u) = -2h2u/(1 - u2)2 - 2g/a
(d/du)2F(u) = -2h2/(1 - u2)2 - 8h2u2/(1 - u2)3 = -2h2(1 + 3u2)/(1 - u2)3
増減表は、次の様に成ります。
| θ | π | π > θ > 0 | 0 |
| u | -1 | -1 < u < +1 | +1 |
| (d/du)2F(u) | -∞ | 負 | -∞ |
| (d/du)F(u) | +∞ | 単調減少 | -∞ |
| F(u) | -∞ | 単調増加後単調減少 | -∞ |
TEC-0-1-56に書かれている考え方でグラフの概形を知る事も出来ます。
特別な場合として、下図の様な場合も考えられます。
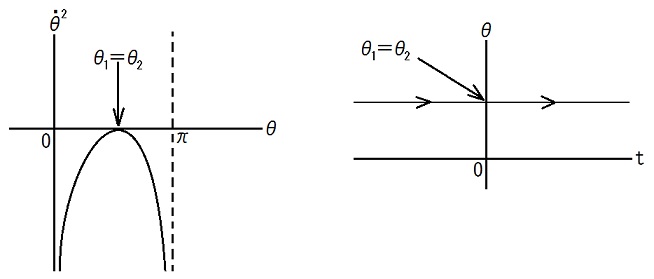
2014.11.13,15,16,19,22
| 11〜17行目の右端に描かれているグラフから、次の事が言えます。 θ1≦θ≦θ2 なるθの値の各々に対しては、グラフから |dθ/dt| が定まります。 θ1 < θ < θ2 なるθの値の各々に対しては、dθ/dt > 0 の場合と dθ/dt < 0 の場合の両方があります。 これは、θ軸上をθの値が、ある時刻にはその点を右向きに(増加しながら)通過し、また別の時刻にはその点を左向きに(減少しながら)通過する、からです。 θ= θ1 と θ = θ2 では dθ/dt = 0 です。 これは、θの値の変化が、θ1では左向き(減少)から右向き(増加)に、θ2では右向き(増加)から左向き(減少)に、向きを変える、からです。 従って、dθ/dt > 0 である様な時刻から話を始めるとθの値は、まずグラフから定まる |dθ/dt| を dθ/dt としてθ2 まで増加し、そこで折り返して今度は、グラフから定まる |dθ/dt| を -dθ/dt としてθ1 まで減少し、そこで再び折り返して、グラフから定まる |dθ/dt| を dθ/dt としてθ2 まで増加し、・・・・という運動(変化)を繰り返す事が分かります。 この様子を描いた物が、24〜28行目のグラフです。 θ = θ1 と成る時刻までは決まりませんが、t = 0 で θ = θ1 という初期条件(30行目)を採用しました。2014.11.15,22 15,16行目の式の成立は、Tが周期である事(17行目)に留意して、次の様に計算すれば分かります。2014.11.15,22 T = (θの値がθ1からθ2まで増加するのに掛かる時間) + (θの値がθ2からθ1まで減少するのに掛かる時間) θの値がθ1からθ2まで増加するのに掛かる時間は、 ∫θ1θ2 dθ dt/dθ = ∫θ1θ2 dθ (dθ/dt)-1 = ∫θ1θ2 dθ |dθ/dt|-1 θの値がθ2からθ1まで減少するのに掛かる時間は、 ∫θ2θ1 dθ dt/dθ = -∫θ1θ2 dθ (dθ/dt)-1 = -∫θ1θ2 dθ (-|dθ/dt|)-1 = ∫θ1θ2 dθ |dθ/dt|-1 ∴ T = 2∫θ1θ2 dθ |dθ/dt|-1 ∴ T/2 = ∫θ1θ2 dθ |dθ/dt|-1 = ∫θ1θ2 dθ [√F(cosθ)]-1 = ∫θ1θ2 dθ [F(cosθ)]-1/2 19,20行目の式の成立は、t = nT から t = nT + T/2 までの間にθの値がθ1 からθ2 まで増加する事(24〜28行目のグラフ)に留意して、θの値がθ1 からθまで増加する時間が t - nT = ∫θ1θ dθ' [F(cosθ')]-1/2 である事を考えれば、分かります。2014.11.15,22 22,23行目の式の成立は、t = nT - T/2 から t = nT までの間にθの値がθ2 からθ1 まで減少する事(24〜28行目のグラフ)に留意して、θの値がθからθ1 まで減少する時間が nT - t = ∫θθ1 dθ' dt/dθ' = -∫θ1θ dθ' (dθ'/dt)-1 = -∫θ1θ dθ' (-|dθ'/dt|)-1 = ∫θ1θ dθ' |dθ'/dt|-1 = ∫θ1θ dθ' [√F(cosθ')]-1 = ∫θ1θ dθ' [F(cosθ')]-1/2 である事を考えれば、分かります。2014.11.15,22 |
||
29,30行目に書かれている様に、
φ = ∫dt dφ/dt = ∫dt h/(sinθ)2
という不定積分を、θ=θ(t)を代入した後で計算すれば、φを t の関数として求める事が出来るはずです。2014.11.16,22
TEC-0-1-23へのコメントが、COM-1-10-18〜21に、TEC-0-1-23-20〜30へのコメントとして、書かれています。
楕円積分の結果を簡単な式で表せない事が原因で、θもφも t の関数として簡単な式で表せなかった事、を受けてのコメントです。2014.11.16,22
【SEOテキスト】2005.12.7更新2005.12.12更新,宇田雄一03.9.24,CAN-1-1-12-1〜11,d/dt[(sinθ)2φ]=2θφ(sinθ)cosθ+(sinθ)2φ=0↑CAN-1-1-12-11∴(sinθ)2φ=h(constant)これをCAN-1-1-12-10に代入すると、aθ-ah2(cosθ)/(sinθ)3=g sinθ両辺に2θをかけると、ad/dtθ2+ah2d/dt 1/(sinθ)2=-2gd/dt cosθ∴θ2=E-h2/(sinθ)2-2g/a cosθ↑const.(エネルギではない)θ2,O,θ1,θ2,π,θ,T/2=∫θ2,θ1,dθ[E-h2/(sinθ)2-2g/a cosθ]-1/2(Tは周期)nT≦t≦nT+T/2では、t=nT+∫θ,θ1,dθ'[E-h2/(sinθ')2-2g/a cosθ']-1/2,nT-T/2≦t≦nTでは、t=nT-∫θ,θ1,dθ'[E-h2/(sinθ')2-2g/a cosθ']-1/2ここで現れた積分は楕円積分と呼ばれるものに帰着し、簡単な式で表せぬ。θ,θ2,θ1,t,O,θがtの関数として求まったのでTEC-0-1-23-5よりφもtの関数として求まる。初期条件としてt=0でθ=θ1,φ=0とする。