
次のページ
前のページ
目次
CAN-1-1-12
TEC-0-1-23
【補足説明欄】
3,4行目の左辺は、TEC-0-1-23-11,12の式の右辺を、u = cosθ(TEC-0-1-56-2)を使って書き換える事によって得られた式であり、TEC-0-1-23-11〜17の右端のグラフに対する補足説明における F(u) に一致します。2014.11.17,19
5行目の式は、3,4行目の式の両辺に 1 - u2 を掛ける事によって得られた式です。2014.11.17
6行目の式の最左辺は、5行目の式の左辺を整理した物です。2014.11.17
6行目で定義されている f(u) は、(1 - u2)F(u) に一致します。
これは、6行目の最左辺が (3,4行目の左辺)×(1 - u2) に等しく、3,4行目の左辺はTEC-0-1-23-11〜17の右端のグラフに対する補足説明における F(u) に等しい、からです。2014.11.17,19
7行目の式は、h = 0 である場合を除外せずに書かれていますが、h = 0 である場合は、dφ/dt = 0(∵TEC-0-1-23-5)だから、鉛直面内の滑らかな円周上に束縛された質点の運動であり、球面振子の問題としてわざわざ本件で取り扱うには値しません。
だから、本件では h ≠ 0 の場合だけを考える事にします。
すると、f(-1) < 0 and f(1) < 0 です。2014.11.18
8〜16行目のグラフの概形の根拠は、f(u) が3次関数であり u3 の係数が正である事と、f(1) < 0 and f(-1) < 0 である事です。
f(u) > 0 なる u が -1 ≦ u ≦ 1 内に必ず有る事までは言えませんが、有る場合には8〜16行目のグラフの様に成らざるを得ません。
この事と、-1 < u < 1 で常に 1 - u2 > 0 である事が、TEC-0-1-23-11〜17の右端のグラフの概形の根拠です。
ただし、ここ(TEC-0-1-56)での考察だけからでは、TEC-0-1-23-11〜17の右端のグラフの -1 < u < 1 部分での F(u) の符号しか分からず、(d/du)2F(u) が常に負である事、等の詳しい特徴は分かりません。
因みに、ここで「8〜16行目のグラフの様に成らざるを得ない」と判断した際の思考内容は、人は考える時には必ず言葉で考える、という主張への反例に成っている、事が分かると思います。
あなたも、知恵の輪を外す時に行なうのと同種の頭の使い方を、したはずです。
これは言葉による思考ではありませんね。
f(u) > 0 なる u が -1 ≦ u ≦ 1 内に全く無い場合であっても下図の様な場合は、球面振子の運動として考察するに値します。
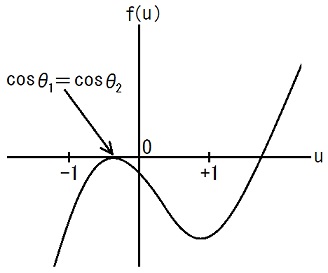
これは、θが一定のまま経時変化しない場合、に該当します。2014.11.17,18,19,22
【SEOテキスト】宇田雄一04.2.22,TEC-0-1-23,CAN-1-1-12-1〜11,u=cosθとおくとE- h2/ 1-u2 -2g/a u=0となるのは、E(1-u2)-h2-(2g/a)u(1-u2)=0,(2g/a)u3-Eu2-(2g/a)u+(E-h2)≡f(u)=0の時。f(-1)=-h2≦0,f(1)=-h2≦0,f(u),cosθ2,-1,O,1,u,cosθ1