
次のページ
前のページ
目次
CAN-1-1-11
TEC-0-1-22
【補足説明欄】
TEC-0-1-22-11,12の式の両辺の逆数を考える事によって、
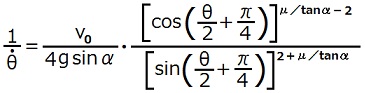
だと分かります。2014.10.26
2〜14行目が μ > tanα の場合について、15〜23行目が μ = tanα の場合について、24〜29行目がμ < tanα の場合についてです。2014.10.29
3,4行目の等号の成立根拠は、TEC-0-1-55補足説明欄冒頭の式です。
7行目以降の積分に持ち込むために、分母と分子にsin(θ/2 + π/4)を掛けておきました。2014.10.25,26
5,6行目の不等号≦の成立理由は、
0≦θ≦π/2 では sin(θ/2 + π/4) ≧ 1/√2 である事、
です。
3 + μ/tanα > 0 である事や、負の因子が無い事も、チェックポイントに成ります。2014.10.25,26
9,10行目の等号の成立は、
φ = θ/2 + π/4,
w = cosφ
と置いて、
(d/dθ){[-2/(μ/tanα - 1)]wμ/tanα-1}
= [-2/(μ/tanα - 1)](dφ/dθ)(dw/dφ)(d/dw)wμ/tanα-1
= [-2/(μ/tanα - 1)](1/2)(-sinφ)(μ/tanα - 1)wμ/tanα-2
= (sinφ)wμ/tanα-2
という風に計算する事によって、確認できます。2014.10.26
13,14行目の不等号≦の成立は、7〜12行目の積分結果と5,6行目の不等号の成立から、言えます。2014.10.25,26
16,17行目の等号の成立は、TEC-0-1-55補足説明欄冒頭の式に μ = tanα(TEC-0-1-55-15)を代入する事によって、得られます。
20行目以降の積分に持ち込むために、分母と分子を[sin(θ/2 + π/4)]2cos(θ/2 + π/4)で割っておきました。2014.10.25,26
18,19行目の不等号≧の成立理由は、
0 < sin(θ/2 + π/4) ≦ 1
∴ [sin(θ/2 + π/4)]-2 ≧ 1
です。
負の因子が存在しない事も、チェックポイントです。2014.10.25,26
20,21行目の等号の成立は、
φ = θ/2 + π/4,
w = tanφ
と置いて、
(d/dθ)(2 ln w)
= 2(dφ/dθ)(dw/dφ)(d/dw)ln w
= 2(1/2)(cosφ)-2|w|-1
= (cosφ)-2/w
という風に計算する事によって、確認できます。2014.10.26
22,23行目の等号(22行目の等号ではない)の成立は、20〜22行目の積分結果と18,19行目の不等号の成立から、言えます。2014.10.25
25,26行目の不等号≧の成立根拠は、TEC-0-1-55補足説明欄冒頭の式と、
[sin(θ/2 + π/4)]-2-μ/tanα ≧ 1 ≧ sin(θ/2 + π/4)
である事です。
TEC-0-1-55補足説明欄冒頭の式に負の因子が存在しない事、もチェックポイントです。2014.10.25,26
27行目について。
7〜10行目については同様ですが、μ < tanα の場合には、11,12行目の様には成りません。
9,10行目の式の角括弧内に θ → π/2 - 0 を代入すると、→ +∞ に成るからです。
この積分結果と25,26行目の不等号の成立から、28,29行目の等号の成立が言えます。2014.10.25
【SEOテキスト】このページは05.11.23に書き直した,宇田雄一04.2.22,CAN-1-1-11-12〜30,TEC-0-1-22,μ>tanαの場合1/θ=v0/4gsinα・sin(θ/2+π/4)・[cos(θ/2+π/4)]μ/tanα-2/[sin(θ/2+π/4)]3+μ/tanα≦v0/4gsinα・sin(θ/2+π/4)・[cos(θ/2+π/4)]μ/tanα-2/(1/√2)3+μ/tanα,∫π/2 0 dθsin(θ/2+π/4)・[cos(θ/2+π/4)]μ/tanα-2=[-2/μ/tanα-1・(cos(θ/2+π/4))μ/tanα-1]π/2 0=2/μ/tanα-1(1/√2)μ/tanα-1∴∫π/2 0 1/θdθ≦v0/4gsinα・2/μ/tanα-1・(√2)4=有限,μ=tanαの場合 1/θ=v0/4gsinα・[sin(θ/2+π/4)]-2[cos(θ/2+π/4)]-2/tan(θ/2+π/4)≧v0/4gsinα・[cos(θ/2+π/4)]-2/tan(θ/2+π/4),∫π/2 0 dθ[cos(θ/2+π/4)]-2/tan(θ/2+π/4)=[2ln tan(θ/2+π/4)]π/2 0=∞∴∫π/2 0 1/θdθ=∞,μ<tanαの場合1/θ≧v0/4gsinαsin(θ/2+π/4)・[cos(θ/2+π/4)]μ/tanα-2ここでTEC-0-1-55-7〜10と同様に考えて、∫π/2 0 1/θdθ=∞以上のように1/θが積分できなくても不等式で答が分かる場合あり。