CAN-1-1-11 初等力学正典 CANONICAL NOTE

CAN-1-1-11

次のページ
前のページ
目次

TEC-0-1-7

TEC-0-1-19

TEC-0-1-20

TEC-0-1-21

TEC-0-1-22

TEC-0-1-55

TEC-0-1-57

TEC-0-1-58

TEC-0-1-59

TEC-0-1-60

【補足説明欄】

1行目から3行目までの項は、CAN-1-1-9-9～14の式の右辺第3項(CAN-1-1-9-9～11の最右項)に、
ω'¹ = -ωcosα, ω'² = 0, ω'³ = ωsinα
を代入して得られた式です。
4行目から6行目までの項は、CAN-1-1-9-9～14の式の右辺第4項(CAN-1-1-9-12～14の左の項)に、
ω'¹ = -ωcosα, ω'² = 0, ω'³ = ωsinα
を代入して得られた式です。
ω'¹ = -ωcosα, ω'² = 0, ω'³ = ωsinα
である事は、CAN-1-1-9-1～3の式と、CAN-1-1-9-4～6の左の式と、CAN-1-1-10-22～24の式と、CAN-1-1-8-12～14の式、から分かります。
まず、CAN-1-1-10-22～24の式と、CAN-1-1-8-12～14の式から、
R₁₁ = (sinα)cos(ωt), R₂₁ = (sinα)sin(ωt), R₃₁ = -cosα,
R₁₂ = -sin(ωt), R₂₂ = cos(ωt), R₃₂ = 0,
R₁₃ = (cosα)cos(ωt), R₂₃ = (cosα)sin(ωt), R₃₃ = sinα
だと分かります。
これを、CAN-1-1-9-1～3の式に、代入すると、
ω¹ = 0, ω² = 0, ω³ = ω
だと分かります。
CAN-1-1-8-15に対する補足説明から R^-1 = R^t だと分かるので、
(R^-1)₁₁ = R₁₁ = (sinα)cos(ωt), (R^-1)₁₂ = R₂₁ = (sinα)sin(ωt), (R^-1)₁₃ = R₃₁ = -cosα,
(R^-1)₂₁ = R₁₂ = -sin(ωt), (R^-1)₂₂ = R₂₂ = cos(ωt), (R^-1)₂₃ = R₃₂ = 0,
(R^-1)₃₁ = R₁₃ = (cosα)cos(ωt), (R^-1)₃₂ = R₂₃ = (cosα)sin(ωt), (R^-1)₃₃ = R₃₃ = sinα
です。
これと、ω¹ = 0, ω² = 0, ω³ = ω と、CAN-1-1-9-4～6の左の式から、
ω'¹ = (R^-1)₁₁ ω¹ + (R^-1)₁₂ ω² + (R^-1)₁₃ ω³ = -ωcosα,
ω'² = (R^-1)₂₁ ω¹ + (R^-1)₂₂ ω² + (R^-1)₂₃ ω³ = 0,
ω'³ = (R^-1)₃₁ ω¹ + (R^-1)₃₂ ω² + (R^-1)₃₃ ω³ = ωsinα
が得られます。
この結果は、また、以下の様に、図形的に求める事も出来ます。
まず、TEC-0-1-16-23,24とCOM-1-18-5～13の図を基にして、TEC-0-1-6-26～30の様に考えれば、
ω＝ωk
だと分かります。
この事とCOM-1-18-14～20の図から、
ω＝-ω(cosα)i' + ω(sinα)k'
だと分かります。
ところが、
ω¹i+ω²j+ω³k=ω'¹i'+ω'²j'+ω'³k' (CAN-1-1-9-4～6に対する補足説明)
ω=ω¹i+ω²j+ω³k (TEC-0-1-16-25～30に対する補足説明)
∴ω＝ω'¹i'+ω'²j'+ω'³k'
であるから、
-ω(cosα)i' + ω(sinα)k'＝ω'¹i'+ω'²j'+ω'³k'
である事に成り、この事とi',j',k'の線形独立性から、
ω'¹ = -ωcosα, ω'² = 0, ω'³ = ωsinα
だと分かります。2013.06.30;2013.07.01,02,03,04,07,09,12,15,16

1行目から3行目までの項を、TEC-0-1-15-24～26に従って計算すれば、

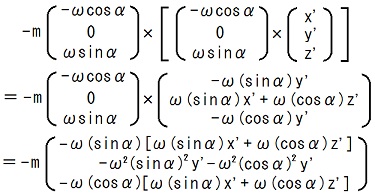
と成ります。2013.07.24

7,8行目の式は、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第1行) = (右辺の計算結果の第1行)
を具体的に書いた物です。
CAN-1-1-11-1～3の項の第1行は、
mω(sinα)[ω(sinα)x'+ω(cosα)z']
である事が、この項についての補足説明から、分かります。
CAN-1-1-11-4～6の項の第1行は、TEC-0-1-15-24～26に従って計算すれば、
-2m(-ωsinα)dy'/dt
だから、CAN-1-1-10-27～CAN-1-1-11-6の式の右辺の計算結果の第1行は、
-ma(cosα)ω²sinα + mω(sinα)[ω(sinα)x' + ω(cosα)z'] - 2m(-ωsinα)dy'/dt
= -maω²(sinα)cosα + mω²(sinα)²x' + mω²(sinα)(cosα)z' + 2mω(sinα)dy'/dt
= m[-aω²(sinα)cosα + ω²(sinα)²x' + ω²(sinα)(cosα)z' + 2ω(sinα)dy'/dt]
= m{-aω²(sinα)cosα + ω²[1 - (cosα)²]x' + ω²(sinα)(cosα)z' + 2ω(sinα)dy'/dt}
= m{-aω²(sinα)cosα + ω²(cosα)[(sinα)z' - (cosα)x'] + ω²x' + 2ω(sinα)dy'/dt}
と成ります。
一方、CAN-1-1-10-27～CAN-1-1-11-6の式の左辺の計算結果の第1行はmd²x'/dt²だから、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第1行) = (右辺の計算結果の第1行)
を具体的に書くと、
m d²x'/dt² = m{-aω²(sinα)cosα + ω²(cosα)[(sinα)z' - (cosα)x'] + ω²x' + 2ω(sinα)dy'/dt}
この式の両辺をmで割れば、7,8行目の式が得られます。
7,8行目の式は、CAN-1-1-10-28の符号ミスに由来するミスを含んでいます。2013.06.20,24;2013.07.17,21,24,28

9行目の式は、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第2行) = (右辺の計算結果の第2行)
を具体的に書いた物です。
CAN-1-1-11-1～3の項の第2行は、
-m[-ω²(sinα)²y' - ω²(cosα)²y'] = mω²y'
である事が、この項についての補足説明から、分かります。
CAN-1-1-11-4～6の項の第2行は、TEC-0-1-15-24～26に従って計算すれば、
-2m[ω(sinα)dx'/dt + ω(cosα)dz'/dt]
だから、CAN-1-1-10-27～CAN-1-1-11-6の式の右辺の計算結果の第2行は、
mω²y' - 2m[ω(sinα)dx'/dt + ω(cosα)dz'/dt] = m[ω²y' - 2ω(sinα)dx'/dt - 2ω(cosα)dz'/dt]
だと分かります。
一方、CAN-1-1-10-27～CAN-1-1-11-6の式の左辺の計算結果の第2行は m d²y'/dt² だから、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第2行) = (右辺の計算結果の第2行)
を具体的に書くと、
m d²y'/dt² = m[ω²y' - 2ω(sinα)dx'/dt - 2ω(cosα)dz'/dt]
この式の両辺をmで割れば、9行目の式が得られます。2013.06.20;2013.07.22,24,29

10,11行目の式は、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第3行) = (右辺の計算結果の第3行)
を具体的に書いた物です。
CAN-1-1-11-1～3の項の第3行は、
mω(cosα)[ω(sinα)x'+ω(cosα)z']
である事が、この項についての補足説明から、分かります。
CAN-1-1-11-4～6の項の第3行は、TEC-0-1-15-24～26に従って計算すれば
2mω(cosα)dy'/dt
だから、CAN-1-1-10-27～CAN-1-1-11-6の式の右辺の計算結果の第3行は、
-mg - ma(cosα)ω²cosα + mω(cosα)[ω(sinα)x' + ω(cosα)z'] + 2mω(cosα)dy'/dt
= -mg - ma(cosα)ω²cosα + m[ω²(sinα)(cosα)x' + ω²(cosα)²z' + 2ω(cosα)dy'/dt]
= m{-g - a(cosα)ω²cosα + ω²(sinα)(cosα)x' + ω²[1 - (sinα)²]z' + 2ω(cosα)dy'/dt}
だと分かります。
一方、CAN-1-1-10-27～CAN-1-1-11-6の式の左辺の計算結果の第3行は m d²z'/dt² だから、CAN-1-1-10-27～CAN-1-1-11-6の式の
(左辺の計算結果の第3行) = (右辺の計算結果の第3行)
を具体的に書くと、
m d²z'/dt² = m{-g - a(cosα)ω²cosα + ω²(sinα)(cosα)x' + ω²[1 - (sinα)²]z' + 2ω(cosα)dy'/dt}
この式の両辺をmで割れば、10,11行目の式が得られます。
10,11行目の式は、CAN-1-1-10-28の符号ミスに由来するミスを含んでいます。2013.06.20,24;2013.07.24,30

7～11行目の式に含まれる、CAN-1-1-10-28の符号ミスに由来するミス、を修正するには、CAN-1-1-11-7～11の式中の a を -a に書き換えるだけで良い事が、CAN-1-1-10-28に対する補足説明に、書かれています。2014.10.30

7～11行目の連立微分方程式を解く事は、TEC-0-1-19-18～TEC-0-1-21-11, TEC-0-1-57～TEC-0-1-60で、行われています。2014.10.30

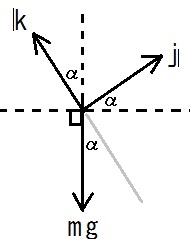
17行目のkは、27～30行目の図の様な、斜面の2つの法線ベクトルのうちで上向きの法線ベクトル、だとします。
重力ベクトルとjとkの位置関係は、下図の様に成ります。
重力ベクトルの灰色線への射影を考える事によって、重力ベクトルのk方向成分は-mg(cosα)だと分かります。
重力ベクトルの先端から灰色線に下した垂線に着目すると、重力ベクトルのj方向成分は-mg(sinα)だと分かります。
以上より、重力ベクトルは-mg(sinα)j-mg(cosα)kだと分かります。2013.10.19,21,22,26,28

20,21行目について。
動摩擦力の向きは速度ベクトルの向きの逆です。
したがって-dr/dtの向きは動摩擦力の向きと同じです。
したがって動摩擦力の向きの単位ベクトルは(-dr/dt)/|-dr/dt|です。
この事と、動摩擦力の大きさがμNである事から、動摩擦力ベクトルは
μN(-dr/dt)/|-dr/dt| = -μN(dr/dt)/|dr/dt|
だと分かります。2013.10.29,30

23行目の式は、TEC-0-1-7-21の最も左の等式に
F¹ = -μN(dx/dt)/|dr/dt|　(理由は下方※に別記しました)
を代入する事によって得られます。2013.10.30;2013.11.07,12

24行目の式は、TEC-0-1-7-21の中央の等式に
F² = -mg(sinα)-μN(dy/dt)/|dr/dt|　(理由は下方※に別記しました)
を代入する事によって得られます。2013.11.03,07,12

25行目の右の等号の成立は、TEC-0-1-7-21の最も右の等式に
F³ = -mg(cosα)+N　(理由は下方※に別記しました)
を代入する事によって分かります。2013.11.03,07,12

※

25行目の左の等号の成立は、26行目に書かれている条件 z = 0 をtで2回微分する事によって、分かります。2013.11.19

12～30行目の問題に対する解答は、TEC-0-1-21-19からTEC-0-1-22-30までに、書かれています。2013.11.20

▲このページの上端へ行く

【SEOテキスト】03.9.15,宇田雄一,第2章,質点の力学,-m(,-ωcosα,0,ωsinα,)×[(,-ωcosα,0,ωsinα,)×(,x',y',z',)]-2m(,-ωcosα,0,ωsinα,)×(,),∴{,=-aω2(sinα)cosα+ω2(cosα)(z'sinα-x'cosα)+ω2x'+2ω(sinα),=ω2y'-2ω(sinα),-2ω(cosα),=-g-aω2(cosα)2-ω2(sinα)(z'sinα-x'cosα)+ω2z'+2ω(cosα),[束縛放物問題],水平とαの角をなす粗い斜面（摩擦係数μ）の上に原点Oがあり、Oを通りi方向の直線が斜面内に収まり、かつ水平で、Oを通りj方向の直線も斜面内に収まり、jが斜面を昇る方向を向いているとする。質点がこの斜面からの抗力と重力mg[-(sinα)j-(cosα)k]のみを受けた結果、t≧0の間ずっと斜面上に存し続け、t=0の瞬間r=0,=v0iだったとすると、t>0における質点の運動は、どうなるか？垂直抗力をNkとすると摩擦力は-μN,/|,|となるから、運動方程式から次式が導かれる(TEC-0-1-7-13～21)mは質量。,m,=-μN,/√,2+,2,m,=-mg sinα-μN,/√,2+,2,0=m,=-mg cosα+N,束縛条件はz=0、初期条件は,(0)=v0,(0)=0,x(0)=y(0)=0です。,k,j,α,水平,α,i(水平),O