
次のページ
前のページ
目次
【補足説明欄】
このページTEC-0-1-60の内容が、CAN-1-1-11-7~11の連立微分方程式の厳密解です。
CAN-1-1-10-19以降に対する補足説明に書かれている様に、静止系での運動方程式を使ってx,y,zを求めた後で、それを座標変換する事によってx',y',z'を求めた場合には、頻出の関数だけを使って解を書く事が出来るでしょう。
TEC-0-1-60の式は、それと同じ事を無限級数で表した物だ、と見なせます。2014.10.31
1~10行目の式には、TEC-0-1-57-18,19の式が誤りである事に由来する誤りが含まれています。
それを正すと、次の様に成ります。
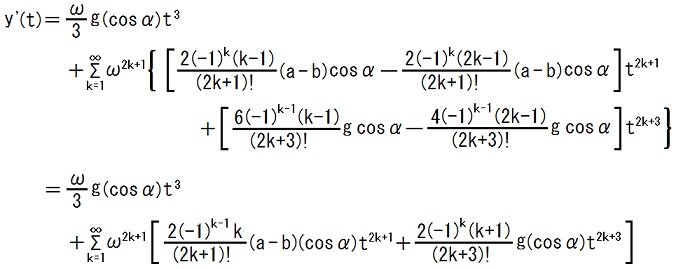
2014.11.02,08
1~10行目の式は、TEC-0-1-19-21の式に、
y'0 = 0 (TEC-0-1-21-3)
y'1 = (1/3)g(cosα)t3 (TEC-0-1-21-5)
y'n = 0 (n = 2, 4, 6, ・・・) ∵TEC-0-1-57-29,30
y'n = antn + bntn+2 (n = 3, 5, 7, ・・・) ∵TEC-0-1-57-27,28
を代入し、得られた式に、TEC-0-1-59-1~8の式から得られる a2k+1 の式と、TEC-0-1-59-20~27の式から得られる b2k+1 の式を代入し、さらに、得られた式に、
α2 = (1/2)(b - a)(cosα)2 ∵ TEC-0-1-57-9,30
β2 = (1/8)g(cosα)2 ∵ TEC-0-1-57-9,30
a3 = -(1/3)(b - a)cosα ∵ TEC-0-1-57-18,19,27(18,19については修正された式)
b3 = -(1/30)g(cosα) ∵ TEC-0-1-57-18,19,27(18,19については修正された式)
を代入する事によって、得られます。2014.10.30;2014.11.08,10
11~20行目の式には、TEC-0-1-57-18,19の式が誤りである事に由来する誤りが含まれています。
それを正すと、次の様に成ります。
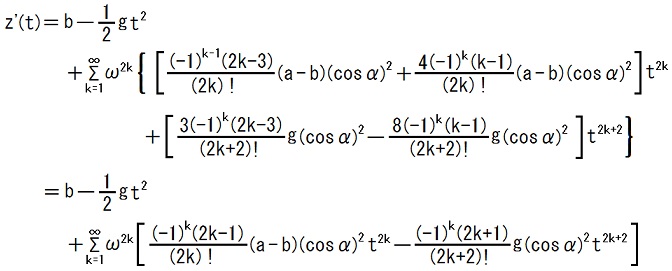
この修正を行う過程で、TEC-0-1-60-11~20にはTEC-0-1-57-18,19の式が誤りである事に由来する誤り以外にも計算ミスが含まれているらしい事、に気付きました。
上掲の式は、そのミスを受け継いでいません。2014.11.02,08,10
11~20行目の式は、TEC-0-1-19-22の式に、
z'0 = b - (1/2)gt2 (TEC-0-1-21-3)
z'1 = 0 (TEC-0-1-21-6)
z'n = 0 (n = 3, 5, 7, ・・・) ∵TEC-0-1-57-27,28
z'n = αntn + βntn+2 (n = 2, 4, 6, ・・・) ∵TEC-0-1-57-29,30
を代入し、得られた式に、TEC-0-1-59-1~8の式から得られる α2k の式と、TEC-0-1-59-20~27の式から得られる β2k の式を代入し、さらに、得られた式に、
α2 = (1/2)(b - a)(cosα)2 ∵ TEC-0-1-57-9,30
β2 = (1/8)g(cosα)2 ∵ TEC-0-1-57-9,30
a3 = -(1/3)(b - a)cosα ∵ TEC-0-1-57-18,19,27(18,19については修正された式)
b3 = -(1/30)g(cosα) ∵ TEC-0-1-57-18,19,27(18,19については修正された式)
を代入する事によって、得られます。2014.10.30;2014.11.08,10
21,22行目の式を得るには、次の様に考えます。
まず、TEC-0-1-19-20の式に、
x'0 = 0 (TEC-0-1-21-3)
x'1 = 0 (TEC-0-1-21-5)
x'n = (tanα)z'n (n ≧ 2) ∵TEC-0-1-57-12
を代入すれば、
x'(t) = Σn=2∞ ωn (tanα)z'n(t)
= (tanα)[Σn=0∞ ωn z'n(t) - z'0(t) - ωz'1(t)]
だと分かります。この式に、
Σn=0∞ ωn z'n(t) = z'(t) (TEC-0-1-19-22)
z'0(t) = b - (1/2)gt2 (TEC-0-1-21-3)
z'1(t) = 0 (TEC-0-1-21-6)
を代入すると、
x'(t) = (tanα)[z'(t) - (b - gt2/2)]
だと分かります。2014.10.30,31
21,22行目の式に、11~20行目の式を代入すれば、x'(t)に対する明示的な級数展開を、得る事が出来ます。2014.10.31
1~22行目の式をCAN-1-1-11-7~11の式に代入する事によって、TEC-0-1-60-1~22の式が本当に解に成っているかどうかを、直接調べる事が出来ます。
TEC-0-1-60-1~22の式に含まれるミスを訂正して得られた補足説明欄の式を使って私が確認すると、ちゃんと解に成っていました。2014.11.09
ここまでで、CAN-1-1-10-28の符号ミスに由来するミス、の修正は全くしていません。2014.11.02
TEC-0-1-57~60の推論に含まれる、CAN-1-1-10-28の符号ミスに由来するミス、を修正するには、TEC-0-1-57~60の式中の a を -a に書き換えるだけで良い事が、CAN-1-1-10-28に対する補足説明に、書かれています。
したがって、TEC-0-1-60の式中の a を -a に書き換えた式が正しい結論だ、と考えられます。2014.10.30,31
【SEOテキスト】宇田雄一04.2.23,y'(t)=ω/3g(cosα)t3+∞∑k=1ω2k+1[(2(-1)k(k-1)/(2k+1)!(a-b)(cosα)+2(-1)k-1(2k-1)/(2k+1)!(a-b)(sinα)2cosα)t2k+1+(6(-1)k-1(k-1)/(2k+3)!・g(cosα)+2(-1)k-1(2k-1)/(2k+3)![1-3(sinα)2]gcosα)t2k+3],z'(t)=b-1/2gt2+∞∑k=1ω2k[((-1)k-1(2k-3)/(2k)!(a-b)(cosα)2+4(-1)k(k-1)/(2k)!(a-b)(sinα)2(cosα)2)t2k+(3(-1)k/(2k+1)!・2k-3/k+1・g/2(cosα)2+2(-1)k/(2k+1)!・k-1/k+1[1-3(sinα)2]g(cosα)2)t2k+2],x'(t)=(tanα)[z'(t)-(b-1/2gt2)]確認済