次のページ
前のページ
目次
CAN-1-1-8
CAN-1-1-9
TEC-0-1-7
TEC-0-1-21
COM-1-18
【補足説明欄】
1行目の [2]色々な力と運動 は、このページの2行目からCAN-1-1-14-18までの記事、のタイトルです。2013.03.10
2行目の ①一様な重力の下での運動 は、このページの3行目からCAN-1-1-12-11までの記事、のタイトルです。2013.03.10
3行目の[放物運動]は、4行目から18行目までの記事、のタイトルです。2013.03.10
9行目の3つの式の導出方法は、F1=0,F2=0,F3=-mgを代入してTEC-0-1-7-13～21を読むと、分かります。2013.03.19;2013.04.01,03
12, 15, 17行目のv01, v02, v03の上付き添え字1, 2, 3は、冪指数(1乗, 2乗, 3乗)ではなく、ベクトルの成分の番号です。2013.04.11,14
14行目から16行目までの式を見れば、
t=0の瞬間のrの値 = x0i + y0j + z0k
t=0の瞬間の dr/dt の値 = v01i + v02j + v03k
だと分かります。2013.04.14
19行目の[Neilの放物線]は、このページの19行目から次ページの11行目までの記事、のタイトルです。2013.03.10
このページの第19行目から次ページの第11行目までの内容についての補足説明が、TEC-0-1-19-18～TEC-0-1-21-11とCOM-1-18に、書かれています。
この問題では、静止系での運動方程式を使ってx,y,zを求めた後で、それを座標変換する事によってx',y',z'を求める事も出来ますが、ここでは、慣性力や摂動法の説明をするために、非慣性系での運動方程式と摂動級数を使ってx',y',z'を求めています。2013.02.19;2013.03.13;2013.06.05
20,21行目の式の成立は、CAN-1-1-8-10の定義式とCOM-1-18の図を基にして、TEC-0-1-21-14～16に書かれている様に考え、
cos(π/2-α)＝sinα, sin(π/2-α)＝cosα
である事を使えば、分かります。2013.04.15,20,21
22,23,24行目の式の成立は、COM-1-18の図を基にして、TEC-0-1-21-14～16に書かれている様に考え、
cos(π/2-α)＝sinα, sin(π/2-α)＝cosα
である事を使えば、分かります。2013.04.16,20,21
25行目の式は、質点に働く力の向きが地球の中心に向かう向きである事と、質点に働く力の大きさがmgである事を、表しています。
この式が、この問題の力の法則(COM-1-5-11～12)を表しています。
COM-1-18の図から、-k'は地球の中心に向かう向きを持つ単位ベクトルだ、と分かります。2013.04.22,23
このページの27行目から次ページの6行目までの式の右辺第1項(CAN-1-1-10-27～29の等号の右隣の項)は、CAN-1-1-9-9～14の式の右辺第1項に、
F1i + F2j + F3k = 0i' + 0j' -mgk' ∵TEC-0-1-7-8, CAN-1-1-4-4, CAN-1-1-10-25
で定まる F1, F2, F3 を、代入して得られた物です。
この事は、a = F1, b = F2, c = F3 を代入してTEC-0-1-18-10～17を読むと、分かります。
まず、TEC-0-1-18-13～17と F1i + F2j + F3k = 0i' + 0j' -mgk' より、
R11F1 + R21F2 + R31F3 = 0, R12F1 + R22F2 + R32F3 = 0, R13F1 + R23F2 + R33F3 = -mg
だと分かります。
この事とTEC-0-1-18-10～12から、
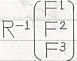
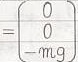
だと分かります。2013.04.23,24,28,29
このページの27行目から次ページの6行目までの式の右辺第2項(CAN-1-1-10-27～29の最右項)は、CAN-1-1-9-9～14の式の右辺第2項に、
x0 = a(cosα)cos(ωt), y0 = a(cosα)sin(ωt), z0 = a(sinα) ∵CAN-1-1-8-11; CAN-1-1-10-20,21
を代入して得られたものです。
その事は、以下の様に考えれば、分かります。
まず、上記の3つの式
x0 = a(cosα)cos(ωt), y0 = a(cosα)sin(ωt), z0 = a(sinα)
をtで繰り返し微分する事によって、
dx0/dt = -aω(cosα)sin(ωt), dy0/dt = aω(cosα)cos(ωt), dz0/dt = 0
= -aω2(cosα)cos(ωt), 
= -aω2(cosα)sin(ωt), 
= 0だと分かります。
故に、
i + j + k = -aω2(cosα)cos(ωt)i -aω2(cosα)sin(ωt)j + 0kこの式に、CAN-1-1-8-12～14の逆変換はTEC-0-1-18-17の等号に対する補足説明の式である事とCAN-1-1-10-22～24、から導かれる式
i = (sinα)cos(ωt)i' -(sinωt)j' + (cosα)cos(ωt)k'
j = (sinα)sin(ωt)i' + (cosωt)j' + (cosα)sin(ωt)k'
k = -(cosα)i' + 0j' + (sinα)k'
を代入すると、
i + j + k= -aω2(cosα)cos(ωt)[(sinα)cos(ωt)i' -(sinωt)j' + (cosα)cos(ωt)k']
-aω2(cosα)sin(ωt)[(sinα)sin(ωt)i' + (cosωt)j' + (cosα)sin(ωt)k']
+ 0[-(cosα)i' + 0j' + (sinα)k']
= -aω2(cosα)(sinα)i' + 0j' - aω2(cosα)(cosα)k'
だと分かります。
これに基づき a =
, b = , c = を代入してTEC-0-1-18-10～17を読みます。まず、TEC-0-1-18-13～17と
i + j + k = -aω2(cosα)(sinα)i' + 0j' - aω2(cosα)(cosα)k' より、R11
+ R21 + R31 = -aω2(cosα)(sinα),R12
+ R22 + R32 = 0,R13
+ R23 + R33 = -aω2(cosα)(cosα)だと分かります。
この事とTEC-0-1-18-10～12から、
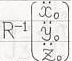
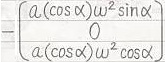
だと分かります。
これに-mを掛けた物が、このページの27行目から次ページの6行目までの式の右辺第2項(CAN-1-1-10-27～29の最右項)であるべきだから、CAN-1-1-10-28の負号(-)は、ミスであり、正号(+)に書き換えられねばなりません。
このミスは、CAN-1-1-11-1～11, TEC-0-1-19-18～TEC-0-1-21-11, TEC-0-1-57～TEC-0-1-60での推論に、受け継がれています。
これらの推論の中の該当箇所を特定し修正して行く事は、大変です。
一つでも見落とすと、その努力は無駄に成ってしまいます。
しかし、CAN-1-1-10-27～29の式を良く見れば、右辺第2項の符号を反転する事は、a を -a に書き換える事と等価です。
だから、この後の推論過程で新規に別のミスが発生していなければ、推論の結果得られた式の中の a を -a に書き換える事によって、大変な修正作業を全く行なう事なく、正しい結果を得る事が出来るはずです。
百行は一案に如かず、です。
したくてしたミスではありませんが、ミスした事が図らずも小技を伝授するのに役立ちました。
転んでもタダでは起きぬ、といった所でしょうか。2013.04.30;2013.05.01,04,06,07,11,12,13,14,15,21,27;2014.10.30,31
【SEOテキスト】宇田雄一,03.9.15,第2章,質点の力学,[2]色々な力と運動,①一様な重力の下での運動,[放物運動],kが鉛直上向きの場合、質量mの質点には常に-mgkの力が働く、という力の法則が成り立つ。ただしgは重力加速度と呼ばれg≒9.8[m/s2]質点に働く-mgkの力は重力と呼ばれる。質点が重力のみを受ける場合には、運動方程式より、,m,=0,m,=0,m,=-mg,が導かれる(TEC-0-1-7-13～21),この連立方程式の一般解は、,x=x0+v01t,y=y0+v02t,z=z0+v03t-(g/2)t2,すなわち、,r=xi+yj+zk=(x0i+y0j+z0k)+(v01i+v02j+v03k)t-(g/2)t2k,ただしx0,y0,z0,v01,v02,v03は積分定数であり、任意。,[Neilの放物線]CAN-1-1-8-4～9-14において、,=0,r0=a(cosα)cos(ωt)i+a(cosα)sin(ωt)j+a(sinα)k,i'=(sinα)cos(ωt)i+(sinα)sin(ωt)j-(cosα)k,j'=-sin(ωt)i+cos(ωt)j,k'=(cosα)cos(ωt)i+(cosα)sin(ωt)j+(sinα)k,F=-mgk'(力の法則),とすると、CAN-1-1-9-9～14の運動方程式は、,m(,)=(,0,0,-mg,)-m(,a(cosα)ω2sinα,0,a(cosα)ω2cosα,)