次のページ
前のページ
目次
CAN-1-1-9
TEC-0-1-17
【補足説明欄】
第3行目の等号の成立根拠は、TEC-0-1-17-23〜25の式の最左辺の第2行第3列と最右辺の第2行第3列が等しい事です。
TEC-0-1-17-23〜25の式の最左辺の第2行第3列＝-ω1,
TEC-0-1-17-23〜25の式の最右辺の第2行第3列＝(
)21(Rt)13+()22(Rt)23+()23(Rt)33＝()21R31+()22R32+()23R33これらが等しい事より、
-ω1＝(
)21R31+()22R32+()23R33だと分かります。2013.03.05,06
第4行目の等号の成立根拠は、TEC-0-1-17-23〜25の式の最左辺の第3行第1列と最右辺の第3行第1列が等しい事です。
TEC-0-1-17-23〜25の式の最左辺の第3行第1列＝-ω2,
TEC-0-1-17-23〜25の式の最右辺の第3行第1列＝(
)31(Rt)11+()32(Rt)21+()33(Rt)31＝()31R11+()32R12+()33R13これらが等しい事より、
-ω2＝(
)31R11+()32R12+()33R13だと分かります。2013.03.05,06
第5行目の等号の成立根拠は、TEC-0-1-17-23〜25の式の最左辺の第1行第2列と最右辺の第1行第2列が等しい事です。
TEC-0-1-17-23〜25の式の最左辺の第1行第2列＝-ω3,
TEC-0-1-17-23〜25の式の最右辺の第1行第2列＝(
)11(Rt)12+()12(Rt)22+()13(Rt)32＝()11R21+()12R22+()13R23これらが等しい事より、
-ω3＝(
)11R21+()12R22+()13R23だと分かります。2013.03.05,06
このページの第10行目から次ページの第7行目までは、CAN-1-1-9-16〜21の式の導出方法の説明です。
CAN-1-1-9-9〜14の式は、
この式の左辺の第1行＝この式の右辺の第1行
この式の左辺の第2行＝この式の右辺の第2行
この式の左辺の第3行＝この式の右辺の第3行
という意味だから、この式については、
[左辺の第1成分(第1行)]i'+[左辺の第2成分(第2行)]j'+[左辺の第3成分(第3行)]k'
＝[右辺の第1成分(第1行)]i'+[右辺の第2成分(第2行)]j'+[右辺の第3成分(第3行)]k'
が成り立ちます。
この事と以下によって、CAN-1-1-9-16〜21の式の成立が、根拠付けられます。
CAN-1-1-9-9〜14の式の左辺の(第1成分)i'+(第2成分)j'+(第3成分)k'は、CAN-1-1-9-16に、一致しています。
TEC-0-1-18-10〜TEC-0-1-19-7には、CAN-1-1-9-9〜14の式の右辺の(第1成分)i'+(第2成分)j'+(第3成分)k'を項別に計算する方法、が書かれています。
CAN-1-1-9-9〜14の式の右辺第1,2項については、TEC-0-1-18-10〜17が該当する説明です。
CAN-1-1-9-9〜14の式の右辺第1項については、a=F1,b=F2,c=F3を代入してTEC-0-1-18-10〜17を読む事によって、
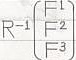の(第1成分)i'+(第2成分)j'+(第3成分)k'=F1i+F2j+F3kである事が、分かります。
この事とTEC-0-1-7-8の式F=F1i+F2j+F3kから、CAN-1-1-9-9〜14の式の右辺第1項については、
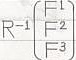の(第1成分)i'+(第2成分)j'+(第3成分)k'=Fだと分かります。
これは、CAN-1-1-9-17と一致します。
CAN-1-1-9-9〜14の式の右辺第2項については、a=-m
,b=-m
,c=-m
を代入してTEC-0-1-18-10〜17を読む事によって、
の(第1成分)i'+(第2成分)j'+(第3成分)k'=-mi-mj-mkである事が、分かります。
この事とCAN-1-1-8-11の式r0=x0i+y0j+z0kをtで2階微分して得られる式から、
の(第1成分)i'+(第2成分)j'+(第3成分)k'=-m
だと分かります。
これは、CAN-1-1-9-18と一致します。
CAN-1-1-9-9〜14の式の右辺第3項については、TEC-0-1-18-18〜22の計算結果を2回繰り返して適用します。
, 
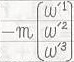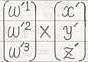を代入した場合と、
, 
を代入した場合、の2回です。まず
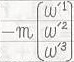と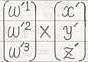を代入した場合の結果から、
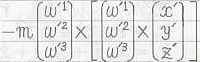の(第1成分)i'+(第2成分)j'+(第3成分)k'=(-mω'1i'-mω'2j'-mω'3k')×[
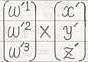の(第1成分)i'+(第2成分)j'+(第3成分)k']だと分かります。
次に、
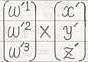とを代入した場合の結果から、の(第1成分)i'+(第2成分)j'+(第3成分)k'=(ω'1i'+ω'2j'+ω'3k')×(x'i'+y'j'+z'k')だと分かります。
両者から、
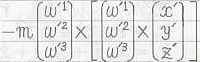の(第1成分)i'+(第2成分)j'+(第3成分)k'=(-mω'1i'-mω'2j'-mω'3k')×[(ω'1i'+ω'2j'+ω'3k')×(x'i'+y'j'+z'k')]
だと分かります。
この結果と、
ω'1i'+ω'2j'+ω'3k'=ω1i+ω2j+ω3k ∵CAN-1-1-9-4〜6の左の式とTEC-0-1-18-10〜17
ω=ω1i+ω2j+ω3k(TEC-0-1-16-25〜30に対する補足説明)
x'i'+y'j'+z'k'=r-r0 ∵r=r0+x'i'+y'j'+z'k'(CAN-1-1-8-5,6)
から、
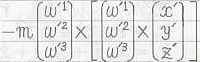の(第1成分)i'+(第2成分)j'+(第3成分)k'=-mω×[ω×(r-r0)]だと分かります。
これは、CAN-1-1-9-19と一致します。
CAN-1-1-9-9〜14の式の右辺第4項については、まずTEC-0-1-18-18〜22の計算結果に、a'=-2mω'1, b'=-2mω'2, c'=-2mω'3; α'=
, β'=
, γ'=
を代入すれば、
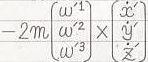の(第1成分)i'+(第2成分)j'+(第3成分)k'=(-2mω'1i'-2mω'2j'-2mω'3k')×(i'+j'+k')だと分かります。
この結果と、
ω'1i'+ω'2j'+ω'3k'=ω1i+ω2j+ω3k ∵CAN-1-1-9-4〜6の左の式とTEC-0-1-18-10〜17
ω=ω1i+ω2j+ω3k(TEC-0-1-16-25〜30に対する補足説明)
から、
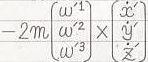の(第1成分)i'+(第2成分)j'+(第3成分)k'=-2mω×(i'+j'+k')だと分かります。
これは、CAN-1-1-9-20と一致します。
TEC-0-1-18-24〜TEC-0-1-19-7は、TEC-0-1-18-18〜22の計算結果をCAN-1-1-9-9〜14の式の右辺第5項に適用するための計算です。
CAN-1-1-9-9〜14の式の右辺第5項については、まずTEC-0-1-18-18〜22の計算結果に、a'=-m
, b'=-m
, c'=-m
; α'=x', β'=y', γ'=z'を代入すれば、
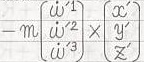の(第1成分)i'+(第2成分)j'+(第3成分)k'=(-mi'-mj'-mk')×(x'i'+y'j'+z'k')だと分かります。
この結果に、
i'+j'+k'=
∵TEC-0-1-19-7x'i'+y'j'+z'k'=r-r0 ∵r=r0+x'i'+y'j'+z'k'(CAN-1-1-8-5,6)
を代入すると、
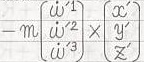の(第1成分)i'+(第2成分)j'+(第3成分)k'=-m×(r-r0)だと分かります。
これは、CAN-1-1-9-21と一致します。2012.12.28,30;2013.01.05,06,07,08,09,12,14,15,18,20,21,22,25,26,28,29,30;2013.02.04
第11行目の左の等号が成り立つのは、R-1=Rt(CAN-1-1-8-15)だからです。
第11行目の右の等号の成立は、行列の掛け算の第1行の計算が
(Rt)11a+(Rt)12b+(Rt)13c=R11a+R21b+R31c
という風に成る事と、行列の掛け算の第2行の計算が
(Rt)21a+(Rt)22b+(Rt)23c=R12a+R22b+R32c
という風に成る事と、行列の掛け算の第3行の計算が
(Rt)31a+(Rt)32b+(Rt)33c=R13a+R23b+R33c
という風に成る事から、分かります。2012.11.11,12
第17行目の等号が成り立つのは、
R11i'+R12j'+R13k'=i
R21i'+R22j'+R23k'=j
R31i'+R32j'+R33k'=k
だからです。
これら3つの式は、以下の様にして導出されます。2012.11.12,13,17,19
R11i'+R12j'+R13k'
=R11(R11i+R21j+R31k)+R12(R12i+R22j+R32k)+R13(R13i+R23j+R33k) ∵CAN-1-1-8-12〜14
=(R11R11+R12R12+R13R13)i+(R11R21+R12R22+R13R23)j+(R11R31+R12R32+R13R33)k
=δ11i+δ12j+δ13k ∵Σn=13RrnRsn=Σn=13Rrn(Rt)ns=(RRt)rs=(13)rs=δrs ∵R-1=Rt(CAN-1-1-8-15)
=1i+0j+0k
=i
R21i'+R22j'+R23k'
=R21(R11i+R21j+R31k)+R22(R12i+R22j+R32k)+R23(R13i+R23j+R33k) ∵CAN-1-1-8-12〜14
=(R21R11+R22R12+R23R13)i+(R21R21+R22R22+R23R23)j+(R21R31+R22R32+R23R33)k
=δ21i+δ22j+δ23k ∵Σn=13RrnRsn=Σn=13Rrn(Rt)ns=(RRt)rs=(13)rs=δrs ∵R-1=Rt(CAN-1-1-8-15)
=0i+1j+0k
=j
R31i'+R32j'+R33k'
=R31(R11i+R21j+R31k)+R32(R12i+R22j+R32k)+R33(R13i+R23j+R33k) ∵CAN-1-1-8-12〜14
=(R31R11+R32R12+R33R13)i+(R31R21+R32R22+R33R23)j+(R31R31+R32R32+R33R33)k
=δ31i+δ32j+δ33k ∵Σn=13RrnRsn=Σn=13Rrn(Rt)ns=(RRt)rs=(13)rs=δrs ∵R-1=Rt(CAN-1-1-8-15)
=0i+0j+1k
=k
第18〜20行目の最も左の式の成立は、TEC-0-1-15-24〜26によります。2012.11.19
第18〜20行目の真ん中の式は、a',b',c'の定義式です。2012.11.19
第18〜20行目の最も右の式は、α',β',γ'の定義式です。2012.11.19
第22行目の等号の成立は、
i'×i'=j'×j'=k'×k'=0, i'×j'=-j'×i'=k', j'×k'=-k'×j'=i', k'×i'=-i'×k'=j' (∵CAN-1-1-8-7〜9)
である事と、TEC-0-1-15-24〜26に対する補足説明の考え方から、分かります。2012.11.19
第23行目の等号の成立根拠は、第13〜17行目の計算の結果から、分かります。
第10〜12行目の式と第18〜20行目の真ん中の式から
a'=R11a+R21b+R31c
b'=R12a+R22b+R32c
c'=R13a+R23b+R33c
だと分かります。
これを使って第13〜17行目の計算の結果を書き換えると、
a'i'+b'j'+c'k'=ai+bj+ck・・・(1)
と成ります。
第10〜12行目でa,b,cをα,β,γに書き換えて得られる式と第18〜20行目の最も右の式から
α'=R11α+R21β+R31γ
β'=R12α+R22β+R32γ
γ'=R13α+R23β+R33γ
だと分かります。
これと、第13〜17行目でa,b,cをα,β,γに書き換えて得られる式から、
α'i'+β'j'+γ'k'=αi+βj+γk・・・(2)
だと分かります。
(1)と(2)から、
(a'i'+b'j'+c'k')×(α'i'+β'j'+γ'k')=(ai+bj+ck)×(αi+βj+γk)
だと分かります。2012.11.20,23,24,27
第25行目の左の等号の成立は、CAN-1-1-9-4〜6の左の式の両辺をtで微分して積の微分法を使うと、分かります。2012.11.27
第25行目の右の等号の成立は、
(d/dt)(R-1)
=(d/dt)(Rt) ∵R-1=Rt(CAN-1-1-8-15)
=(dR/dt)t
と考えれば、分かります。
という書き方では、(d/dt)(Rt)のことなのか(dR/dt)tのことなのか、どちらなのか分かりませんが、ここでは両者が等しいので、そういう書き方をしました。2012.12.04,08,09,21第27行目の3つの等式は、TEC-0-1-16-23,24の式です。2012.12.09
第28〜30行目の左の式は、TEC-0-1-16-25〜27の式です。2012.12.10
第28〜30行目の右の式は、TEC-0-1-17-20〜22の式です。
第28〜30行目の左の式から右の式を導出する方法は、TEC-0-1-17-20〜22に対する補足説明に、書かれています。2012.12.11,14
【SEOテキスト】03.9.1宇田雄一[問題29]次式の根拠がどこに書かれているか述べよ。ω1=-R31R21-R32R22-R33R23,ω2=-R11R31-R12R32-R13R33,ω3=-R21R11-R22R12-R23R13答:TEC-0-1-17-23〜25の式の第2行第3列、第3行第1列、第1行第2列。[問題30]CAN-1-1-9-16〜21の式を導出せよ。R-1(abc)=Rt(abc)=(R11a+R21b+R31c,R12a+R22b+R32c,R13a+R23b+R33c),(R11a+R21b+R31c)i'+(R12a+R22b+R32c)j'+(R13a+R23b+R33c)k'=a(R11i'+R12j'+R13k')+b(R21i'+R22j'+R23k')+c(R31i'+R32j'+R33k')=ai+bj+ck//(a'b'c')×(α'β'γ')=(b'γ'-c'β',c'α'-a'γ',a'β'-b'α'),(a'b'c')=R-1(abc),(α'β'γ')=R-1(αβγ),(b'γ'-c'β')i'+(c'α'-a'γ')j'+(a'β'-b'α')k'=(a'i'+b'j'+c'k')×(α'i'+β'j'+γ'k')=(ai+bj+ck)×(αi+βj+γk)//(ω'1ω'2ω'3)=dR-1/dt(ω1ω2ω3)+R-1(ω1ω2ω3)=Rt(ω1ω2ω3)+R-1(ω1ω2ω3),di'/dt=ω×i',dj'/dt=ω×j',dk'/dt=ω×k'より、(R1iR2iR3i)=(ω1ω2ω3)×(R1iR2iR3i)∴R=(0,-ω3,ω2,ω3,0,-ω1,-ω2,ω1,0)R