
次のページ
前のページ
目次
CAN-1-1-8
【補足説明欄】
第1,2行目の記事は、前頁の第28,29行目の記事の続きです。2012.01.25,31
第1,2行目の左の式の成立は、次の様に考えれば分かります。2012.02.13,14,19,26,27,28
1=i'・i' (CAN-1-1-8の補足説明欄に書かれている様にi'は単位ベクトルだから)
=(R11i+R21j+R31k)・(R11i+R21j+R31k) ∵CAN-1-1-8-12
=(R11)2i・i+R11R21i・j+R11R31i・k+R21R11j・i+(R21)2j・j+R21R31j・k+R31R11k・i+R31R21k・j+(R31)2k・k
=(R11)2+(R21)2+(R31)2 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk1Rk1
1=j'・j' (CAN-1-1-8の補足説明欄に書かれている様にj'は単位ベクトルだから)
=(R12i+R22j+R32k)・(R12i+R22j+R32k) ∵CAN-1-1-8-13
=(R12)2i・i+R12R22i・j+R12R32i・k+R22R12j・i+(R22)2j・j+R22R32j・k+R32R12k・i+R32R22k・j+(R32)2k・k
=(R12)2+(R22)2+(R32)2 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk2Rk2
1=k'・k' (CAN-1-1-8の補足説明欄に書かれている様にk'は単位ベクトルだから)
=(R13i+R23j+R33k)・(R13i+R23j+R33k) ∵CAN-1-1-8-14
=(R13)2i・i+R13R23i・j+R13R33i・k+R23R13j・i+(R23)2j・j+R23R33j・k+R33R13k・i+R33R23k・j+(R33)2k・k
=(R13)2+(R23)2+(R33)2 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk3Rk3
0=i'・j' (CAN-1-1-8の補足説明欄に書かれている様にi'とj'は直交するから)
=(R11i+R21j+R31k)・(R12i+R22j+R32k) ∵CAN-1-1-8-12,13
=R11R12i・i+R11R22i・j+R11R32i・k+R21R12j・i+R21R22j・j+R21R32j・k+R31R12k・i+R31R22k・j+R31R32k・k
=R11R12+R21R22+R31R32 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk1Rk2=Σk=13Rk2Rk1
0=j'・k' (CAN-1-1-8の補足説明欄に書かれている様にj'とk'は直交するから)
=(R12i+R22j+R32k)・(R13i+R23j+R33k) ∵CAN-1-1-8-13,14
=R12R13i・i+R12R23i・j+R12R33i・k+R22R13j・i+R22R23j・j+R22R33j・k+R32R13k・i+R32R23k・j+R32R33k・k
=R12R13+R22R23+R32R33 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk2Rk3=Σk=13Rk3Rk2
0=k'・i' (CAN-1-1-8の補足説明欄に書かれている様にk'とi'は直交するから)
=(R13i+R23j+R33k)・(R11i+R21j+R31k) ∵CAN-1-1-8-14,12
=R13R11i・i+R13R21i・j+R13R31i・k+R23R11j・i+R23R21j・j+R23R31j・k+R33R11k・i+R33R21k・j+R33R31k・k
=R13R11+R23R21+R33R31 ∵i・i=j・j=k・k=1, i・j=i・k=j・i=j・k=k・i=k・j=0
=Σk=13Rk3Rk1=Σk=13Rk1Rk3
第1,2行目のRtは、Rの転置行列であり、
(Rt)ij≡Rji
で定義されます。2012.03.04
第1,2行目のR-1は、Rの逆行列であり、
R-1R=RR-1=13
で定義されます。
ただし、3行3列の単位行列を13と書きました。2012.03.06
第1,2行目の式Rt=R-1の成立は、RtRが単位行列に成る事を示す事によって、証明できます。
RtRが単位行列に成る事は、[(Rt)R]ij=δijを示す事によって、証明できます。
[(Rt)R]ij=δijの成立は、次の様に考えれば、分かります。2012.02.29,2012.03.02
[(Rt)R]ij=Σk=13(Rt)ikRkj=Σk=13RkiRkj=δij
第5行目の式i'・i'=j'・j'=k'・k'=1の成立根拠は、i'もj'もk'も単位ベクトルである事です。
i'もj'もk'も単位ベクトルである事は、CAN-1-1-8の補足説明欄に書かれています。2012.04.21
第6,7行目の式は、次の様にして導出されます。2012.04.22,25
0=d1/dt=(d/dt)(i'・i') ∵1=i'・i'
=(di'/dt)・i'+i'・(di'/dt) ∵積の微分法
=2i'・(di'/dt)
∴i'・(di'/dt)=0
0=d1/dt=(d/dt)(j'・j') ∵1=j'・j'
=(dj'/dt)・j'+j'・(dj'/dt) ∵積の微分法
=2j'・(dj'/dt)
∴j'・(dj'/dt)=0
0=d1/dt=(d/dt)(k'・k') ∵1=k'・k'
=(dk'/dt)・k'+k'・(dk'/dt) ∵積の微分法
=2k'・(dk'/dt)
∴k'・(dk'/dt)=0
第8~10行目で定義されているω1,ω2,ω3は、i',j',k'の角速度(CAN-1-1-3-25~29)です。
第6,7行目の式からi'⊥di'/dt,j'⊥dj'/dt,k'⊥dk'/dtが言えるので、TEC-0-1-7-2,3に対する補足説明の様に考えれば、この様なω1,ω2,ω3が存在する事が、分かります。2012.04.29,30;2012.05.09
第11,12行目の式は、i'・j'=j'・k'=k'・i'=0の全ての辺をtで微分する事によって得られます。
i'・j'=j'・k'=k'・i'=0の成立根拠は、i',j',k'が互いに直交する事です。
i',j',k'が互いに直交する事は、CAN-1-1-8の補足説明欄に書かれています。2012.05.11
第13行目の左の式の成立は、
0=(d/dt)(i'・j') ∵第11,12行目の式
=(di'/dt)・j'+i'・(dj'/dt) ∵積の微分法
=(ω1×i')・j'+i'・(ω2×j') ∵第9,10行目の式
という風に考えれば分かります。2012.05.13,14
第13行目の右の式の成立は、第13行目の左の式から出発して、
0=(ω1×i')・j'+i'・(ω2×j')
=(ω1×i')・j'+(ω2×j')・i' ∵i'・(ω2×j')=(ω2×j')・i'・・・内積の対称性
=ω1・(i'×j') ∵(ω1×i')・j'=ω1・(i'×j')・・・ベクトル三重積の公式
+ω2・(j'×i') ∵(ω2×j')・i'=ω2・(j'×i')・・・ベクトル三重積の公式
=ω1・k'+ω2・(-k') ∵i'×j'=k', j'×i'=-k'
=(ω1-ω2)・k'
という風に考えると、分かります。2012.05.15,16,19
第14行目の左の式の成立は、
0=(d/dt)(j'・k') ∵第11,12行目の式
=(dj'/dt)・k'+j'・(dk'/dt) ∵積の微分法
=(ω2×j')・k'+j'・(ω3×k') ∵第9,10行目の式
という風に考えれば分かります。2012.05.14
第14行目の右の式の成立は、第14行目の左の式から出発して、
0=(ω2×j')・k'+j'・(ω3×k')
=(ω2×j')・k'+(ω3×k')・j' ∵j'・(ω3×k')=(ω3×k')・j'・・・内積の対称性
=ω2・(j'×k') ∵(ω2×j')・k'=ω2・(j'×k')・・・ベクトル三重積の公式
+ω3・(k'×j') ∵(ω3×k')・j'=ω3・(k'×j')・・・ベクトル三重積の公式
=ω2・i'+ω3・(-i') ∵j'×k'=i', k'×j'=-i'
=(ω2-ω3)・i'
という風に考えると、分かります。2012.05.20
第15行目の左の式の成立は、
0=(d/dt)(k'・i') ∵第11,12行目の式
=(dk'/dt)・i'+k'・(di'/dt) ∵積の微分法
=(ω3×k')・i'+k'・(ω1×i') ∵第9,10行目の式
という風に考えれば分かります。2012.05.14
第15行目の右の式の成立は、第15行目の左の式から出発して、
0=(ω3×k')・i'+k'・(ω1×i')
=(ω3×k')・i'+(ω1×i')・k' ∵k'・(ω1×i')=(ω1×i')・k'・・・内積の対称性
=ω3・(k'×i') ∵(ω3×k')・i'=ω3・(k'×i')・・・ベクトル三重積の公式
+ω1・(i'×k') ∵(ω1×i')・k'=ω1・(i'×k')・・・ベクトル三重積の公式
=ω3・j'+ω1・(-j') ∵k'×i'=j', i'×k'=-j'
=(ω3-ω1)・j'
という風に考えると、分かります。2012.05.22
第16行目の式の成立根拠は、第13行目の右の式です。
第13行目の右の式から、ω1-ω2はk'に垂直なベクトルである事、が分かります。
k'に垂直なベクトルはi'とj'の線形結合で表されるはずだから、ω1-ω2はi'とj'の線形結合で表される、と分かります。
ω1-ω2=α1i'+α2j'+α3k'と置けば(ω1-ω2)・k'=0からα3=0を示せる、と考える事も出来ます。2012.05.23,25,28
第17行目の式の成立根拠は、第14行目の右の式です。
第14行目の右の式から、ω2-ω3はi'に垂直なベクトルである事、が分かります。
i'に垂直なベクトルはj'とk'の線形結合で表されるはずだから、ω2-ω3はj'とk'の線形結合で表される、と分かります。
ω2-ω3=β1i'+β2j'+β3k'と置けば(ω2-ω3)・i'=0からβ1=0を示せる、と考える事も出来ます。2012.05.28
第18行目の式の成立根拠は、第15行目の右の式です。
第15行目の右の式から、ω3-ω1はj'に垂直なベクトルである事、が分かります。
j'に垂直なベクトルはk'とi'の線形結合で表されるはずだから、ω3-ω1はk'とi'の線形結合で表される、と分かります。
ω3-ω1=γ1i'+γ2j'+γ3k'と置けば(ω3-ω1)・j'=0からγ2=0を示せる、と考える事も出来ます。2012.05.28
第19行目の内容を詳しく書くと、次の様に成ります。
②+③より、ω2-ω1=γ1i'+β2j'+(β3+γ3)k'
この式の左辺は-(①の左辺)だから、右辺は-(①の右辺)に等しいはずです。
γ1i'+β2j'+(β3+γ3)k'=-(α1i'+α2j')
∴(γ1+α1)i'+(β2+α2)j'+(β3+γ3)k'=0
この式とi',j',k'の線形独立性によって、
γ1+α1=0, β2+α2=0, β3+γ3=0
だと分かります。2012.06.03,04
第20行目の左の式は、②にβ2=-α2を代入する事によって、得られます。2012.06.04
第20行目の右の式は、③にγ3=-β3, γ1=-α1を代入する事によって、得られます。2012.06.05
第21行目の式の成立は、次の様に考えれば、分かります。
第20行目の左の式から、ω2+α2j'=ω3+β3k'が得られる。
第20行目の右の式から、ω1-α1i'=ω3+β3k'が得られる。2012.06.05,06
第22行目の「このベクトルをωと書く」とは、ω=ω1-α1i'=ω2+α2j'=ω3+β3k'と置く、という意味です。2012.06.08,09
第23,24行目の左の式の成立は、
di'/dt=ω1×i' ・・・第9,10行目の左の式
=(ω+α1i')×i' ∵ω1=ω+α1i' ∵第21,22行目
=ω×i'+α1i'×i' ∵外積の分配則
=ω×i' ∵i'×i'=0
という風に考えれば分かります。2012.06.09,11
第23,24行目の中央の式の成立は、
dj'/dt=ω2×j' ・・・第9,10行目の左の式
=(ω-α2j')×j' ∵ω2=ω-α2j' ∵第21,22行目
=ω×j'-α2j'×j' ∵外積の分配則
=ω×j' ∵j'×j'=0
という風に考えれば分かります。2012.06.11
第23,24行目の右の式の成立は、
dk'/dt=ω3×k' ・・・第9,10行目の左の式
=(ω-β3k')×k' ∵ω3=ω-β3k' ∵第21,22行目
=ω×k'-β3k'×k' ∵外積の分配則
=ω×k' ∵k'×k'=0
という風に考えれば分かります。2012.06.11
第25行目から第30行目までの式に現れる列ベクトル同士の積×は、TEC-0-1-15-24~26で定義されています。
ω1,ω2,ω3はベクトルωの成分であり、ω=ω1i+ω2j+ω3kで定義されます。
TEC-0-1-7の第8行目に対する補足説明を参照してください。2012.06.15,16,18
第25行目から第27行目までの式の成立は、以下の様に考えれば、分かります。2012.06.12,13,16,18,19,20
di'/dt=ω×i'より(dR11/dt)i+(dR21/dt)j+(dR31/dt)k=(ω1i+ω2j+ω3k)×(R11i+R21j+R31k) ∵CAN-1-1-8-12
dj'/dt=ω×j'より(dR12/dt)i+(dR22/dt)j+(dR32/dt)k=(ω1i+ω2j+ω3k)×(R12i+R22j+R32k) ∵CAN-1-1-8-13
dk'/dt=ω×k'より(dR13/dt)i+(dR23/dt)j+(dR33/dt)k=(ω1i+ω2j+ω3k)×(R13i+R23j+R33k) ∵CAN-1-1-8-14
これら3つの式をまとめて書くと、
(dR1i/dt)i+(dR2i/dt)j+(dR3i/dt)k=(ω1i+ω2j+ω3k)×(R1ii+R2ij+R3ik); i=1,2,3
この式の右辺は、TEC-0-1-6-20~23(および、これについての補足説明)と同様の方法で計算すれば、
(ω1i+ω2j+ω3k)×(R1ii+R2ij+R3ik)=(ω2R3i-ω3R2i)i+(ω3R1i-ω1R3i)j+(ω1R2i-ω2R1i)k
だから、
(dR1i/dt)i+(dR2i/dt)j+(dR3i/dt)k=(ω2R3i-ω3R2i)i+(ω3R1i-ω1R3i)j+(ω1R2i-ω2R1i)k
∴ [dR1i/dt-(ω2R3i-ω3R2i)]i+[dR2i/dt-(ω3R1i-ω1R3i)]j+[dR3i/dt-(ω1R2i-ω2R1i)]k=0
この式とi,j,kの線形独立性によって、
dR1i/dt-(ω2R3i-ω3R2i)=0, dR2i/dt-(ω3R1i-ω1R3i)=0, dR3i/dt-(ω1R2i-ω2R1i)=0
∴ dR1i/dt=ω2R3i-ω3R2i, dR2i/dt=ω3R1i-ω1R3i, dR3i/dt=ω1R2i-ω2R1i
第29行目の左の等号は、第25行目から第27行目までの式の両辺に左からR-1を掛け、
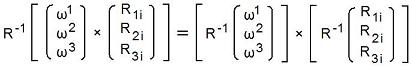
である事(外積を取った後で回転しても、回転した後で外積を取っても、同じに成る事)と、CAN-1-1-9-4~6の左の式
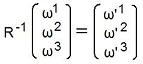
を使うと、分かります。
外積を取った後で回転しても回転した後で外積を取っても同じに成る事は、まず矢印ベクトルの外積で考え、その結果を成分表示に書き直せば、分かります。
u,vを2つの矢印ベクトルとする時、u,v,u×vに共通の回転を施してもこれらの位置関係は変わらないので、
u×vを回転して得られるベクトル=(uを回転して得られるベクトル)×(vを回転して得られるベクトル)
です。
この事を基にして、
u×vを回転して得られるベクトルの成分列ベクトル
=[(uを回転して得られるベクトル)×(vを回転して得られるベクトル)]の成分列ベクトル
=(uを回転して得られるベクトルの成分列ベクトル)×(vを回転して得られるベクトルの成分列ベクトル) ∵TEC-0-1-15-24~26に対する補足説明
という風に考えます。
uとしてω1i'+ω2j'+ω3k'を考え、vとしてR1ii'+R2ij'+R3ik'を考えます。
すると、u'=ω1i+ω2j+ω3kとv'=R1ii+R2ij+R3ikおよびu'×v'は、それぞれu,v,u×vに共通の回転を施して得られるベクトルです。
成分表示の基底としてi',j',k'を用いれば、これらについては、
uを回転して得られるベクトルの成分列ベクトル = R-1(uの成分列ベクトル) ∵ω'1, ω'2, ω'3の定義式と同じ考え方
vを回転して得られるベクトルの成分列ベクトル = R-1(vの成分列ベクトル) ∵ω'1, ω'2, ω'3の定義式と同じ考え方
u×vを回転して得られるベクトルの成分列ベクトル
=R-1(u×vの成分列ベクトル) ∵上の2つの式と同じ考え方
=R-1[(uの成分列ベクトル)×(vの成分列ベクトル)] ∵TEC-0-1-15-24~26に対する補足説明
だから、
u×vを回転して得られるベクトルの成分列ベクトル=(uを回転して得られるベクトルの成分列ベクトル)×(vを回転して得られるベクトルの成分列ベクトル)
という式を具体的に書くと、
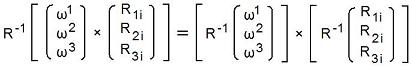
という風に成ります。
この事は、Rが直交行列である事(Rt=R-1)と列ベクトル同士の外積の定義(TEC-0-1-15-24~26)から、直接的に導く事も出来ます。
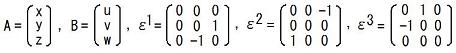
とすると、列ベクトル同士の外積は
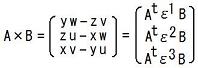
と書けます。
従って、直交行列Pに対してP(A×B)=(PA)×(PB)が成り立つ事は、
Σk=13 Pjk(AtεkB)= (PA)tεjPB
が成り立つ事と同値です。
ところが、
(PA)tεjPB = AtPtεjPB
だから、Σk=13 Pjkεk=PtεjPを示せば、P(A×B)=(PA)×(PB)を示せた事に成ります。
(Ptε1P)rs = Σi=13 Σk=13 (Pt)ri(ε1)ikPks= Σi=13 Σk=13 Pir(ε1)ikPks=P2r1P3s+P3r(-1)P2s=P2rP3s-P3rP2s
(Ptε2P)rs = Σi=13 Σk=13 (Pt)ri(ε2)ikPks= Σi=13 Σk=13 Pir(ε2)ikPks=P1r(-1)P3s+P3r1P1s=P3rP1s-P1rP3s
(Ptε3P)rs = Σi=13 Σk=13 (Pt)ri(ε3)ikPks= Σi=13 Σk=13 Pir(ε3)ikPks=P1r1P2s+P2r(-1)P1s=P1rP2s-P2rP1s
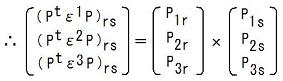
Pt = P-1かつdet P = +1である様な直交行列Pと、(r,s,i) = (1,2,3), (2,3,1), (3,1,2)に対しては、
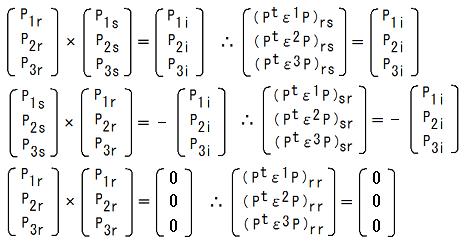
これらと以下を比較する事によって、Σk=13 Pjkεk=PtεjPだと分かります。
(Σk=13 Pjkεk)rs=Σk=13 Pjk(εk)rs=Pji(εi)rs=Pji
(Σk=13 Pjkεk)sr=Σk=13 Pjk(εk)sr=Pji(εi)sr=-Pji
(Σk=13 Pjkεk)rr=Σk=13 Pjk(εk)rr=0
これで、 Pt = P-1かつdet P = +1である様な直交行列Pに対して、P(A×B)=(PA)×(PB)である事を示せました。
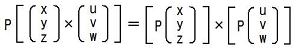
この結果に、P=R-1, x=ω1, y=ω2, z=ω3, u=R1i, v=R2i, w=R3iを代入すると、
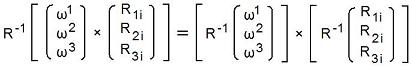
が得られます。
P=R-1がPt=P-1を満たす事は、
(R-1)t=(Rt)t ∵R-1=Rt(TEC-0-1-16-1,2)
=R
=(R-1)-1
という風に考えれば、分かります。
P=R-1がdet P=+1を満たす事は、次の様に考えれば、分かります。
Rt=R-1だから、(det R)2=(det R)(det Rt)=(det R)(det R-1)=det(RR-1)=det 13=1 ∴det R=+1 or -1
i=i',j=j',k=k'の場合、R=13だからdet R=+1で、この状態からi,j,kとi',j',k'の位置関係を連続的に変化させると、Rの行列要素は連続的に変化するので、det Rが+1から-1へと飛躍する事はありません。
したがって常に、det R=+1
∴det (R-1)=(det R)-1=+1
ただし、3行3列の単位行列を13と書きました。
Pt = P-1かつdet P = +1である様な直交行列Pと、(r,s,i) = (1,2,3), (2,3,1), (3,1,2)に対して、
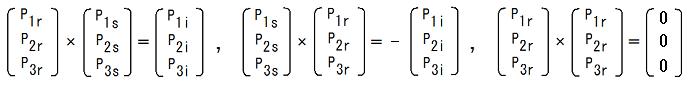
が成り立つ事は、
(P1ri+P2rj+P3rk)×(P1si+P2sj+P3sk)=(P1ii+P2ij+P3ik)
(P1si+P2sj+P3sk)×(P1ri+P2rj+P3rk)=-(P1ii+P2ij+P3ik)
(P1ri+P2rj+P3rk)×(P1ri+P2rj+P3rk)=0
の成立に還元して以下の様に考えれば、TEC-0-1-15-24~26に対する補足説明に書かれている関係を通して、分かります。
|P1ri+P2rj+P3rk|2=(P1r)2+(P2r)2+(P3r)2=(Pt)r1P1r+(Pt)r2P2r+(Pt)r3P3r=(PtP)rr=(P-1P)rr=δrr=1
∴ |P1ri+P2rj+P3rk|=1
同様にして、
|P1si+P2sj+P3sk|=1
|P1ii+P2ij+P3ik|=1
したがって、(P1ri+P2rj+P3rk),(P1si+P2sj+P3sk),(P1ii+P2ij+P3ik)は、いずれも単位ベクトルです。
(P1ri+P2rj+P3rk)・(P1si+P2sj+P3sk)=P1rP1s+P2rP2s+P3rP3s=(Pt)r1P1s+(Pt)r2P2s+(Pt)r3P3s=(PtP)rs=(P-1P)rs=δrs=0
同様にして、
(P1si+P2sj+P3sk)・(P1ii+P2ij+P3ik)=0
(P1ii+P2ij+P3ik)・(P1ri+P2rj+P3rk)=0
したがって、 (P1ri+P2rj+P3rk),(P1si+P2sj+P3sk),(P1ii+P2ij+P3ik)は互いに直交します。
これで、(P1ri+P2rj+P3rk),(P1si+P2sj+P3sk),(P1ii+P2ij+P3ik)は互いに直交する3つの単位ベクトルである事が示されたので、
(P1ri+P2rj+P3rk)×(P1si+P2sj+P3sk) = (P1ii+P2ij+P3ik) or -(P1ii+P2ij+P3ik)
ところが、
[(P1ri+P2rj+P3rk)×(P1si+P2sj+P3sk)]・(P1ii+P2ij+P3ik) = det P = +1
だから、
(P1ri+P2rj+P3rk)×(P1si+P2sj+P3sk) = (P1ii+P2ij+P3ik)
でしか有り得ません。
これと外積の性質によって、
(P1si+P2sj+P3sk)×(P1ri+P2rj+P3rk)=-(P1ri+P2rj+P3rk)×(P1si+P2sj+P3sk)=-(P1ii+P2ij+P3ik)
である事も分かります。
(P1ri+P2rj+P3rk)×(P1ri+P2rj+P3rk)=0
の成立は、同じベクトル同士の外積はゼロベクトルの成る事から、言えます。
2012.06.20,22,24,25,28,30;20120701,02,03,06,07,09,12,13,14,16,17,22,23;2012.08.09,11,12,13,14,15,17,18,19,21,22,25,26,27,28,31;2012.10.16,23
第29行目の右の等号の成立は、
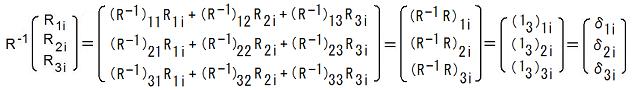
という風に考える事によって、分かります。(13は3行3列の単位行列です)
この事は、一々計算しなくても、R-1(Rの第i列)=(R-1R)の第i列、という風に考えれば、直ぐに分かります。2012.09.01,02,03,05
【SEOテキスト】03.9.1宇田雄一3∑k=1RkiRkj=δij∴Rt=R-1(Rは直交行列である)[問題28]CAN-1-1-8-25~30の等式を導出せよ。i'・i'=j'・j'=k'・k'=1をtで微分すると、i'・di'/dt=j'・dj'/dt=k'・dk'/dt=0故にω1=ω1(t),ω2=ω2(t),ω3=ω3(t)が存在し、di'/dt=ω1×i',dj'/dt=ω2×j',dk'/dt=ω3×k',d/dt(i'・j')=d/dt(j'・k')=d/dt(k'・i')=0より、(ω1×i')・j'+i'・(ω2×j')=0∴(ω1-ω2)・k'=0,(ω2×j')・k'+j'・(ω3×k')=0∴(ω2-ω3)・i'=0,(ω3×k')・i'+k'・(ω1×i')=0∴(ω3-ω1)・j'=0故にω1-ω2=α1i'+α2j'・・・・・・①ω2-ω3=β2j'+β3k'・・・・・・②ω3-ω1=γ3k'+γ1i'・・・・・・③,②+③=-①よりγ1=-α1,β2=-α2,β3+γ3=0∴ω2-ω3=-α2j'+β3k',ω3-ω1=-β3k'-α1i'∴ω1-α1i'=ω2+α2j'=ω3+β3k'このベクトルをωと書くことにすると、di'/dt=ω×i',dj'/dt=ω×j',dk'/dt=ω×k'∴(R1iR2iR3i)=(ω1ω2ω3)×(R1iR2iR3i)(i=1,2,3)∴R-1(R1iR2iR3i)=(ω'1ω'2ω'3)×[R-1(R1iR2iR3i)]=(ω'1ω'2ω'3)×(δ1iδ2iδ3i)