次のページ
前のページ
目次
TEC-0-1-15
TEC-0-1-16
TEC-0-1-17
【補足説明欄】
第2,3行目の根拠は、TEC-0-1-15の[問題26]に書かれています。2012.01.08
第4行目の ③座標変換と慣性力 は、このページの第4行目から次ページの第21行目までの記事のタイトルです。2012.01.08
第5行目の等号は、CAN-1-1-1-11で説明されています。2012.01.09
第6行目の式は、原点としてO'を採用し、i,j,kの代わりにi',j',k'を採用した場合の、デカルト座標を(x',y',z')とする、という意味です。2012.01.13
第7行目から第9行目まで、について。
i',j',k'はi,j,kに共通の回転を施して得られるベクトルの組だから、i',j',k'も互いに直交する3つの単位ベクトルで右手系を成します。2012.01.14
第12行目から第14行目までの式を成り立たせる9個の実数R11,R12,R13,R21,R22,R23,R31,R32,R33が存在する、と考えて良いのは、どんなベクトルもi,j,kの線形結合で表せるはずだからです。
i'をi,j,kの線形結合で表せるはずだから、第12行目の式を成り立たせるR11,R21,R31が存在する、と考えられます。
j'をi,j,kの線形結合で表せるはずだから、第13行目の式を成り立たせるR12,R22,R32が存在する、と考えられます。
k'をi,j,kの線形結合で表せるはずだから、第14行目の式を成り立たせるR13,R23,R33が存在する、と考えられます。
i',j',k'の向きは一般には時々刻々変化するので、R11,R12,R13,R21,R22,R23,R31,R32,R33は、いずれも時刻tの関数です。
「一般には」という言葉の意味は、CAN-1-1-3の補足説明欄で、説明されています。2012.01.17,20,23
第15行目の理由は、TEC-0-1-15-28～TEC-0-1-16-2の[問題27]で、説明されています。
直交行列とは、転置行列と逆行列が等しい実行列、のことです。2012.01.15,16,18
第16～18行目の左の式は、第5,6,11,12,13,14行目の式から導き出されます。
第5,6行目の式に第11,12,13,14行目の式を代入すると、
r=xi+yj+zk
=(x0i+y0j+z0k)+x'(R11i+R21j+R31k)+y'(R12i+R22j+R32k)+z'(R13i+R23j+R33k)
=(x0+R11x'+R12y'+R13z')i+(y0+R21x'+R22y'+R23z')j+(z0+R31x'+R32y'+R33z')k
∴[x-(x0+R11x'+R12y'+R13z')]i+[y-(y0+R21x'+R22y'+R23z')]j+[z-(z0+R31x'+R32y'+R33z')]k=0
この式とi,j,kの線形独立性によって、
x-(x0+R11x'+R12y'+R13z')=0, y-(y0+R21x'+R22y'+R23z')=0, z-(z0+R31x'+R32y'+R33z')=0
∴x=x0+R11x'+R12y'+R13z', y=y0+R21x'+R22y'+R23z', z=z0+R31x'+R32y'+R33z'
この式を行列を使って表現すると、
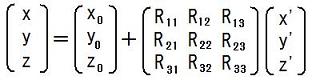
2012.03.10,11,12,2012.04.10
第19～24行目の左の式は、第16～18行目の左の式をtで2階微分する事によって、得られます。
をξと略記し、
をξ0と略記し、
をξ'と略記すると、第16～18行目の左の式はξ=ξ0+Rξ'と書けます。この式をtで1階微分すると、
dξ/dt=dξ0/dt+(d/dt)(Rξ')
=dξ0/dt+(dR/dt)ξ'+R(dξ'/dt) ∵(d/dt)(Rξ')=(dR/dt)ξ'+R(dξ'/dt)・・・積の微分法
この式をtでもう1階微分すると、
d2ξ/dt2
=d2ξ0/dt2+(d/dt)[(dR/dt)ξ']+(d/dt)[R(dξ'/dt)]
=d2ξ0/dt2
+[(d2R/dt2)ξ'+(dR/dt)(dξ'/dt)] ∵(d/dt)[(dR/dt)ξ']=(d2R/dt2)ξ'+(dR/dt)(dξ'/dt)・・・積の微分法
+[(dR/dt)(dξ'/dt)+R(d2ξ'/dt2)] ∵(d/dt)[R(dξ'/dt)=(dR/dt)(dξ'/dt)+R(d2ξ'/dt2)・・・積の微分法
=d2ξ0/dt2+(d2R/dt2)ξ'+2(dR/dt)(dξ'/dt)+R(d2ξ'/dt2)
これは第19～24行目の左の式です。2012.03.13,2012.04.02,13,14,16,17,18
第26,29行目の記号×は列ベクトル同士の外積を表し、その定義は、TEC-0-1-15-24～26に、書かれています。2013.02.18
第25行目から第30行目までの式の成立根拠は、TEC-0-1-16-4～TEC-0-1-17-28で解説されています。2012.04.20
脚注の「TECH-0-1-15～17」は誤りです。正しくは「TEC-0-1-15～17」です。
【SEOテキスト】宇田雄一,03.8.12,第2章,質点の力学,(2)曲面上の運動,fが保存力の場合にはf=-∇Uとすると、mv2/2+Uは時間が経過しても変化しない。,③座標変換と慣性力,k'(t),j'(t),r=xi+yj+zk=r0+x'i'+y'j'+z'k',k,i'(t),O'(t),右図参照。i',j',k'はi,j,kに共通の回転を施して得られるベクトルの組、,j,i,O,r0はr0=r0(t)≡,→,OO',の事とする。r0=x0i+y0j+z0kとし、,{,i'=R11i+R21j+R31k,j'=R12i+R22j+R32k,k'=R13i+R23j+R33k,とすると、R=R(t)は直交行列であり、,(,x,y,z,)=(,x0,y0,z0,)+R(,x',y',z',),{,≡d2x0/dt2,≡d2y0/dt2,≡d2z0/dt2,(,)=(,)+,(,x',y',z',)+2,(,)+R(,),{,≡dx'/dt,≡dy'/dt,≡dz'/dt,≡d2x'/dt2,≡d2y'/dt2,≡d2z'/dt2,(,)=R-1(,)-R-1(,)+(,ω'1,ω'2,ω'3,)×[(,x',y',z',)×(,ω'1,ω'2,ω'3,)]-2(,ω'1,ω'2,ω'3,)×(,)-(,)×(,x',y',z',)