
次のページ
前のページ
目次
CAN-1-1-9
TEC-0-1-16
TEC-0-1-19
【補足説明欄】
第1行目から第3行目までの式の成立根拠は、TEC-0-1-16-28〜30がR-1(dR/dt)の第i列の計算と見なせる事です。2012.09.07,08,09
TEC-0-1-16-28〜30の式に、i=1を代入する事によって、
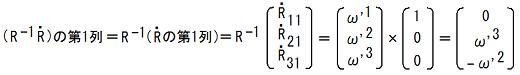
TEC-0-1-16-28〜30の式に、i=2を代入する事によって、
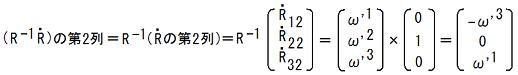
TEC-0-1-16-28〜30の式に、i=3を代入する事によって、
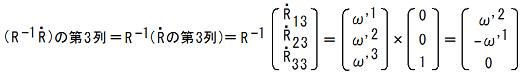
この事は、TEC-0-1-19-9〜16でも、言及されています。2013.02.19;2013.02.19
第5行目から第7行目までの式の成立は、次の様に考えれば、分かります。
第1行目から第3行目までの式で右辺の行列をΩと書けば、
R-1(dR/dt)=Ω
この式の両辺に左からRを掛ければ、
dR/dt=RΩ
この式の両辺をtで微分して積の微分法を使うと、
(d/dt)2R=(dR/dt)Ω+R(dΩ/dt)
これは、第5行目から第7行目までの式です。2012.09.10,23,25
第8行目から第10行目までの式の成立は、第5行目から第7行目までの式の両辺に左からR-1を掛けた後で、第1行目から第3行目までの式を代入すると、分かります。2012.09.10
第12行目から第14行目までの式の成立は、左辺に第1〜3行目の式を代入したものが、右辺をTEC-0-1-19-10〜12に従って変形したものに等しい事、を確認する事によって分かります。2012.09.10,26,29
第15行目から第17行目までの式の成立は、左辺に第8行目から第10行目までの式を代入したものが、右辺をTEC-0-1-19-10〜12に従って変形したものに等しい事、を確認する事によって分かります。2012.09.10,30
CAN-1-1-8-19〜24の式の両辺に左からR-1を掛けた後で、TEC-0-1-17-12〜17の式を代入して整理すると、CAN-1-1-8-25〜30の式が得られます。2012.09.10,2012.10.01
第20行目から第22行目までの式の成立は、TEC-0-1-19-10〜12を使ってTEC-0-1-16-25〜27の式を書き換えた後で、TEC-0-1-19-13〜15の考え方を使うと、分かります。2012.09.22
TEC-0-1-17を読み終わった直ぐ後に読むべき補足説明が、TEC-0-1-18-1〜7に[問題29]として、書かれています。2013.02.19
【SEOテキスト】宇田雄一03.9.1∴R-1R=(0,-ω'3,ω'2,ω'3,0,-ω'1,-ω'2,ω'1,0)さらに、R=R(0,-ω'3,ω'2,ω'3,0,-ω'1,-ω'2,ω'1,0)+R(0,-ω'3,ω'2,ω'3,0,-ω'1,-ω'2,ω'1,0)∴R-1R=(0,-ω'3,ω'2,ω'3,0,-ω'1,-ω'2,ω'1,0)2+(0,-ω'3,ω'2,ω'3,0,-ω'1,-ω'2,ω'1,0)であるから、R-1R(x'y'z')=(ω'1ω'2ω'3)×(x'y'z'),R-1R(x'y'z')=(ω'1ω'2ω'3)×[(ω'1ω'2ω'3)×(x'y'z')]+(ω'1ω'2ω'3)×(x'y'z')残るはCAN-1-1-9-1〜3の確認のみだ。TEC-0-1-16-25〜27により、R=(0,-ω3,ω2,ω3,0,-ω1,-ω2,ω1,0)R∴(0,-ω3,ω2,ω3,0,-ω1,-ω2,ω1,0)=RR-1=RRt∴ω1=(RRt)32=R31R21+R32R22+R33R23,ω2=(RRt)13=R11R31+R12R32+R13R33,ω3=(RRt)21=R21R11+R22R12+R23R13