次のページ
前のページ
目次
CAN-1-1-10
CAN-1-1-11
TEC-0-1-15
TEC-0-1-17
【補足説明欄】
第2行目の左の等号は、前ページの第28～30行目の右の等式の両辺を転置して得られる式
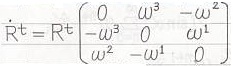
の、左辺を
に掛けた結果と、右辺をに掛けた結果が等しい事を、表しています。2012.12.16,17,21第2行目の右の等号が成り立つのは、
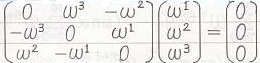
だからです。2012.12.18,21
第4行目から第6行目までの式の成立根拠は、第1～3行目の式と前頁の第24～26行目の式です。2012.12.21
第7行目の式の左の等号の成立根拠は、第4～6行目の式と前頁の第10～17行目です。
a=
, b=
, c=
である場合については、TEC-0-1-19-4～6とTEC-0-1-18-10～12によって、
R11a+R21b+R31c=
R12a+R22b+R32c=
R13a+R23b+R33c=
だと分かります。
この結果をTEC-0-1-18-13～17の計算結果に代入すれば、TEC-0-1-19-7の式の左の等号の成立が分かります。2012.12.22,25,26;2013.02.08
第7行目の式の右の等号の成立は、
ω=ω1i+ω2j+ω3k(TEC-0-1-16-25～30に対する補足説明)
をtで微分する事によって、分かります。2013.02.08
19行目の「ωは十分に小さい」とは、20行目から22行目までの式の右辺の無限級数が収束する程度にωが小さい、という意味です。2013.05.28
20行目の式はωの冪級数で、x'0(t), x'1(t), x'2(t), x'3(t), ・・・はその係数だ、と見なされ得ます。
ωの関数のテイラー級数展開と考えても構いません。
もちろん、ωは定数であり、求めているtの関数をこの形に書いたのだから、この式をtの関数と見る方が自然な第一の見方ですが、どうしてこの置き方を思い付けるのか、という発想法の観点と、この置き方で十分に一般的なのか、という探索範囲の観点からは、ωの冪級数という考え方が、有効です。
この様な級数を摂動級数と呼びます。
この式を使ってx'(t)を求める事は、円周率の小数表示を求める事に、似ています。
ωは非常に小さいので、第n+1項は第n項に比べて桁違いに小さく成ります。
第n項以降を切り捨てれば、円周率の小数点以下n-1項まで求めた近似に相当する近似が、得られます。
21,22行目の式についても同様です。
ただし、20,21,22行目の式は3つで1セットに成っており、本問の場合には、まずx'0(t), x'1(t), x'2(t), x'3(t), ・・・を求め、その後でy'0(t), y'1(t), y'2(t), y'3(t), ・・・を求め、最後にz'0(t), z'1(t), z'2(t), z'3(t), ・・・を求める、という風に3つを切り離して別々に求める事、は出来ません。
一般に、パラメータωを含む方程式がω＝0の場合に正確に解けるならば、解をωの冪級数の形に書いておいてωの係数関数を求める事によってω≠0の場合の解を求める方法、を摂動法と呼びます。
摂動法は、有限項のみ求めて近似解を得る、という風に使われるのが普通ですが、摂動法で一般項を求めて厳密解を得る事が出来る場合もあります。
摂動法には、ωの値がいくら大きくても成り立つ、とは限らない、という欠点があります。2013.05.29;2013.06.02,03,04,05,09
24行目から29行目までの式は、20行目から22行目までの式をCAN-1-1-11-7,8の式に代入して得られる式です。
この式は、CAN-1-1-10-28の符号ミスに由来するミスを含んでいます。2013.06.08,11,16;2013.08.01
【SEOテキスト】宇田雄一03.9.2,Rt(ω1ω2ω3)=Rt(0,ω3,-ω2,-ω3,0,ω1,ω2,-ω1,0)(ω1ω2ω3)=(000)∴(ω'1ω'2ω'3)=R-1(ω1ω2ω3),ω'1i'+ω'2j'+ω'3k'=ω1i+ω2j+ω3k=ω,TEC-0-1-15-24～26,17-1～3外積の行列表現,(abc)×(αβγ)=(0,-c,b,c,0,-a,-b,a,0)(αβγ)さらに(0,-c,b,c,0,-a,-b,a,0)(α1α2α3β1β2β3γ1γ2γ3)の第k列=(0,-c,b,c,0,-a,-b,a,0)(αkβkγk)このテクニックは覚えておこう。CAN-1-1-10-19～11-11摂動法,ωは十分に小さいものとする。x'(t)=x'0(t)+ωx'1(t)+ω2x'2(t)+ω3x'3(t)+・・・・・・・,y'(t)=y'0(t)+ωy'1(t)+ω2y'2(t)+ω3y'3(t)+・・・・・・・,z'(t)=z'0(t)+ωz'1(t)+ω2z'2(t)+ω3z'3(t)+・・・・・・・と置いてCAN-1-1-11-7～11に代入すると、∞∑n=0ωnx'n=-aω2(sinα)cosα+(sinα)(cosα)∞∑n=0ωn+2z'n-(cosα)2∞∑n=0ωn+2x'n+∞∑n=0ωn+2x'n+2(sinα)∞∑n=0ωn+1y'n