次のページ
前のページ
目次
TEC-0-1-18
TEC-0-1-19
COM-1-10
【補足説明欄】
第1行目から第3行目までの式の成立根拠は、TEC-0-1-17-18〜28に書かれています。2012.10.02
第4行目から第6行目までの左の定義式は、ω'1, ω'2, ω'3をω1i+ω2j+ω3k=ω'1i'+ω'2j'+ω'3k'で定義する事と等価です。
ω1i+ω2j+ω3k=ω'1i'+ω'2j'+ω'3k'から第4〜6行目の左の定義式を導く方法は、CAN-1-1-8-6の等号とCAN-1-1-8-12〜14の式からCAN-1-1-8-16〜18の左の式を導く方法と同様です。2012.10.15,16
第7行目の式は、TEC-0-1-7-15の式です。2012.10.24,27
第9行目から第14行目までの式は、CAN-1-1-8-25〜30の式の両辺にmを掛けた後で、右辺第1項に、CAN-1-1-9-7の式の成分表示
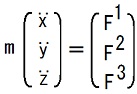
を代入すると、得られます。
ただし、右辺第3項の符号と外積の順序にも、気を付けて下さい。
この部分は、筆記ミスではありません。
外積の順序を変えると結果の符号が変わるので、外積の順序と符号の両方を変えれば、結果は変わりません。2012.10.28,29,30
第16行目から第21行目までの式は、第9行目から第14行目までの式を、矢印ベクトルの形式に直したものです。
第16行目から第21行目までの式の導出方法は、TEC-0-1-18-9〜TEC-0-1-19-7に書かれています。
また、第16行目から第21行目までの式についての補足説明は、COM-1-10-1〜10にも、書かれています。
2012.11.03,05,06;2013.02.05
この部分（座標変換と慣性力）について、当正典の解説法は、伝統的な普通の解説法とは違います。
伝統的な普通の解説法には欠点があるからです。
伝統的な普通の解説法と当正典の解説法の関係について知りたい場合には、日本物理学会2004年春季大会での私の発表27pWQ-1の報告記事を御覧下さい。200?.??.??;2013.02.05
伝統的な普通の解説法が具体的にはどういうものなのか、当正典サイト内にはまだ書かれていないので、これを将来補筆するつもりです。ゴールドスタイン著「新版・古典力学・上」吉岡書店
で言うと、232ページに書かれている説明が、伝統的な普通の解説法です。【SEOテキスト】03.8.31,宇田雄一,第2章,質点の力学,ただし、ω1≡R21,+R22,+R23,ω2≡R31,+R32,+R33,ω3≡R11,+R12,+R13,(,ω'1,ω'2,ω'3,)≡R-1(,ω1,ω2,ω3,),(,)≡,d,-,dt,(,ω'1,ω'2,ω'3,),以上の結果にF1i+F2j+F3k=m(,i+,j+,k)を代入すると、,m(,)=R-1(,F1,F2,F3,)-mR-1(,)-m(,ω'1,ω'2,ω'3,)×[(,ω'1,ω'2,ω'3,)×(,x',y',z',)]-2m(,ω'1,ω'2,ω'3,)×(,)-m(,)×(,x',y',z',),これより,m(,i'+,j'+,k')=F-m,狭義慣性力,-mω×[ω×(r-r0)],遠心力,-2mω×(,i'+,j'+,k'),コリオリの力,-m,×(r-r0)