
次のページ
前のページ
目次
TEC-0-1-38
TEC-0-1-39
【補足説明欄】
2~8行目の図は、CAN-1-1-13-26~30の記事の続きです。
この図について、TEC-0-1-37-26~30に、補足説明があります。2015.11.25
9行目の「④電磁力」は、10~18行目の記事のタイトルです。2016.02.01
10行目の位置ベクトル x は、3次元ベクトルです。
当典以外では x に単位を含めますが、当典では x は大きさや成分が(全くの数学上の)数である様なベクトルだ、と考えます。
MKSA単位系では、位置ベクトルの大きさや各成分の単位は [m] です。2016.02.05
10行目の t は、実数(全くの数学上の数)です。
MKSA単位系では、時刻の単位は [s] です。
当典以外では、例えば t = 3.2[s] という風に、t に単位が含められますが、当典では、例えば t = 3.2 という風に、t に単位を含めません。2016.02.05
11行目の E(x, t) と H(x, t) は、どちらも3次元ベクトルです。
当典以外では、E(x, t) や H(x, t) に単位を含めますが、当典では、E(x, t) も H(x, t) も大きさや成分が(全くの数学上の)数である様なベクトルだ、と考えます。
MKSA単位系では、電場の大きさや各成分の単位は [kg・m・s-3・A-1] であり、磁場の大きさや各成分の単位は [A/m] です。2016.02.04
12行目の q は、実数です。
実数でありさえすれば良く、正(プラス)である必要は有りません。
MKSA単位系では、電荷の単位は [A・s] です。
当典以外では、例えば q = 3.2[A・s] という風に、q に単位が含められますが、当典では、例えば q = 3.2 という風に、q に単位を含めません。2016.02.04,05
12行目の m は、正(プラス)の実数です。
MKSA単位系では、質量の単位は [kg] です。
当典以外では、例えば m = 3.2[kg] という風に、m に単位が含められますが、当典では、例えば m = 3.2 という風に、m に単位を含めません。2016.02.05
14行目の r は、質点の位置ベクトルです。
当典以外では r に単位を含めますが、当典では r は大きさや成分が(全くの数学上の)数である様なベクトルだ、と考えます。
MKSA単位系では、位置ベクトルの大きさや各成分の単位は [m] です。2016.02.01,05
14行目の記号×は、ベクトルの外積を表しています。2016.02.04
第 14 行目について。
ベクトルとして矢印ではなく成分を考えるとき、基底として右手系 i - j - k (CAN-1-1-1-11~16) を用いるのか、それを空間的に反転した左手系 i’- j’- k’ ( i’=-i ,j’=-j ,k’=-k ) を用いるのかによって、ローレンツ力の法則の形が異なるだろうか?
右手系 i - j - k を用いた場合の、ローレンツ力の成分を F とし、位置ベクトルの成分を r とし、磁場の成分を H とすると、左手系 i’- j’- k’ を用いた場合の、ローレンツ力の成分は F’=-F であり、位置ベクトルの成分は r’=-r であり、磁場の成分は H’=-H ではないのか?
そうだとすると、F=μ0 q(dr/dt)×H ⇔ -F’=μ0 q(dr’/dt)×H’
と成ってしまうが、それで良いのか?
実は H’=-H が間違っています。
正しくは F’=-F, r’=- r, H’=H です。
そのため、F=μ0 q(dr/dt)×H ⇔ F’=μ0 q(dr’/dt)×H’
であり、右手系と左手系でローレンツ力の法則の形は同じに成ります。
それでは H1i + H2j + H3k = H'1i' + H'2j' + H'3k' という風に成らないではないか、という疑問に対する答えは、「はい、成りません」です。
この点については、CAN-3-1-11-9,10で学びます。
成分同士の外積はTEC-0-1-15-24~26で定義されています。2008.7.27;2008.7.29;2016.02.01,04,08,09
15行目の内容は、両者の合力をローレンツ力と呼ぶ人は私以外には居ないかもしれない、という点で、間違っているかもしれません。2016.02.08
17行目のμ0 は、見ての通り実数(全くの数学上の数)です。
当典以外では、μ0 = 4π× 10-7[kg・m・s-2・A-2] という風に、μ0に単位が含められます。????.??.??;2016.02.01,04,05
18行目の B は、磁束密度と呼ばれます。
磁束密度は3次元ベクトルです。
MKSA単位系では、磁束密度の大きさや各成分の単位は [kg・s-2・A-1] です。2016.02.05,08
| CAN-1-1-1の補足説明欄に単位ベクトルの説明として、当典では文法主義は採用しない、と書きましたが、このページに至って、どうしても文法主義的な記号法を避ける事が出来なく成りました。 「当典以外では・・・当典では・・・」という部分が、それです。 文法主義的な書き方というのは、例えば、縦 x[m], 横y[m]の長方形の面積はxy[m2]だ、という風に表現する書き方です。 文法主義的でない普通の書き方では、面積は x[m]×y[m] だ、という風に書かれますね。 つまり、文法主義では掛け算等の数学の演算は必ず全くの数学上の数同士で行なう、のに対して、普通の書き方では (長さ)×(長さ) の様な、物理量の間の演算を考える、という事です。 このページ以前では、普通の書き方に従っているつもりで補足説明を記入して来ましたが、CAN-1-1-14-16,17を見て、手書き部分が文法主義的な書き方に成っている事、に気付くと同時に、ここ以降を文法主義的でない普通の書き方で精密に書くのは困難だ、と感じました。 いくら物理量の間の演算を直接考えても、途中で必ず数学上の演算を使うので、何も省略せずに書く、という私の方針では、どうしても文法主義的な書き方に成ります。 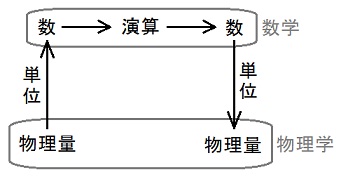 そして、説明の分からない所を無くすには、何も省略せずに書く、という姿勢が不可避だ、と思っています。 とは言っても、3cmは長さですが、3は長さではありません。 そういう意味で、E を電場だとしておきながら、E の大きさは無次元の数だとするのは、精密な理解としては間違いです。 文法主義の用語法では、cmという座標系での3cmという長さの座標は3だ、と言います。 このページの x, t, E(x, t), H(x, t), q, m, r は全て、そういう意味での座標です。 学校への提出物は、普通の書き方で書いて下さい。2016.02.05,08,09 |
9~18行目の記事についての例題と解答が、TEC-0-1-38に挙げられています。2016.02.01
CAN-1-1-1
CAN-2-1-2
CAN-3-1-2
CAN-3-1-11
【SEOテキスト】宇田雄一,第2章,質点の力学,φ,O,θ+,θ-,θ-=-θ+,b,④電磁力,任意の位置xと時刻tに対して、tにおけるxでの電場の値と磁場の値がE(x,t)とH(x,t)ならば、電荷q質量mを持つ質点が電場から受けると力と磁場から受ける力は、それぞれ、,qE(r,t)とμ0q,×H(r,t)である。両者の合力または後者のみをローレンツ力と呼ぶ。ただしμ0は真空透磁率であり、MKSA単位系ではμ0=4π×10-7,μ0HをBと書く。