
次のページ
前のページ
目次
【補足説明欄】
1〜8行目の式は、前ページの28〜31行目の漸化式を解いて得られた式です。
cosα を c と略記している事が、29行目に書かれています。
本文は一般項をどの様に推測したかが分かる様な式で書かれていますが、これが漸化式の解に成っている事を確認する為には、分数を約分しておいた方が便利です。
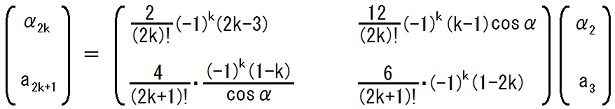
確認では途中で、
(2k+1)!(k+1) = (2k+1)!(2k+2)/2 = (2k+2)!/2
である事を使います。2014.10.29,30;2014.11.05
10,11行目の式は、前ページの8行目の式を書き直した物です。2014.10.29
12,13行目の等号の成立は、前ページの19行目の式から分かります。2014.10.29
14,15行目の等号の成立は、12,13行目の右辺に10,11行目の式を代入すれば、分かります。2014.10.29
16〜19行目の式は、10〜15行目の計算結果を、行列を用いて書き換えた物です。2014.10.29
20〜27行目の式は、16〜19行目の漸化式を解いて得られた式です。
cosα を c と略記している事が、29行目に書かれています。
本文は一般項をどの様に推測したかが分かる様な式で書かれていますが、これが漸化式の解に成っている事を確認する為には、分数を約分しておいた方が便利です。
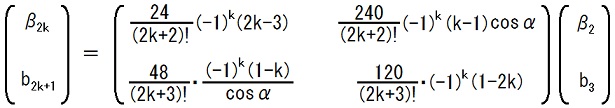
約分には、
(2k+1)!(k+1) = (2k+1)!(2k+2)/2 = (2k+2)!/2
である事を使いました。
確認では途中で、
(2k+3)!(k+2) = (2k+3)!(2k+4)/2 = (2k+4)!/2
である事を使います。2014.10.29,30;2014.11.05
1〜8行目の式と20〜27行目の式を得る際には、導き出したのではなくて、大体こんな感じではないか、という見当を付けて、それを漸化式に代入して違う所を修正した、のだったと思います。
最初の数項を具体的に書き出して、それを見て一般項を推測し、その推測が正しい事を漸化式で検証した、というのだったかも。
9,28行目にOKと書いてある事と、漸化式と解の間に何も書いていない事を見て、そう思いました。
何と無くそうだった様な記憶も、かすかにあります。
解が見付かって良かった、見付からなかったらお手上げだった、運が良かった、確認時にハラハラした、といった感想を持った気がします。2014.10.29,30;2014.11.05
【SEOテキスト】宇田雄一04.2.23,(α2k,a2k+1)=1/k!(2kk!/(2k)!・(-1)k(2k-3)/2k-1 2kk!/(2k+1)!・(-1)k-1(k-1)/2k-2c,3・2kk!/(2k)!・(-1)k(k-1)/2k-2c 3・2kk!/(2k+1)!・(-1)k-1(2k-1)/2k-1)(α2,a3)OK,β2k+2=cosα/k+2b2k+1+1/(2k+3)(2k+4)β2k,b2k+3=-2/cosα/2k+5β2k+2+1/(2k+4)(2k+5)b2k+1,(β2k+2,b2k+3)=1/k+2(1/2/2k+3 cosα,-1/cosα/(2k+3)(2k+5) -3/2/2k+5)(β2k,b2k+1),(β2k,b2k+1)=2/(k+1)!(3・2kk!/(2k+1)!・(-1)k/2k-1(2k-3),3・2k+1(k+1)!/(2k+3)!・(-1)k-1/2k-2・k-1/c,15・2kk!/(2k+1)!・(-1)k/2k-2(k-1)c,(2k-1)15・2k+1(k+1)!/(2k+3)!・(-1)k-1/2k-1)(β2,b3)OK,c≡cosα