
次のページ
前のページ
目次
CAN-1-1-13
TEC-0-1-29
TEC-0-1-30
TEC-0-1-31
TEC-0-1-32
TEC-0-1-33
TEC-0-1-34
TEC-0-1-35
TEC-0-1-37
TEC-0-1-39
【補足説明欄】
2行目の等号は、CAN-1-1-13-27の等号です。2015.11.16
3行目のθ0 は、TEC-0-1-34-28,29のθ0 です。2015.11.16
3行目の等号の成立根拠は、
θ(t → +∞) = θ0 ∵TEC-0-1-35-1〜14VIIのグラフと、TEC-0-1-32-1,2の式
θ(t → -∞) = -θ0 ∵TEC-0-1-35-1〜14VIIのグラフと、TEC-0-1-32-1,2の式
である事です。
TEC-0-1-35-1〜14VIIのグラフ中の矢印が時間経過の向きを表している事、に気を付けて下さい。2015.11.16,30;2016.02.01
4,5行目の等号の成立は、CAN-1-1-13-28,29の式に、θ- = -θ0 を代入する事によって分かります。
θ- = -θ0 である事は、θ- の定義式(CAN-1-1-13-27)と、θ(t → -∞) = -θ0 である事、から分かります。
θ(t → -∞) = -θ0 である事は、TEC-0-1-35-1〜14VIIのグラフとTEC-0-1-32-1,2の式から、分かります。
TEC-0-1-35-1〜14VIIのグラフ中の矢印が時間経過の向きを表している事、に気を付けて下さい。2015.11.16,29,30;2016.02.01
6,7行目の等号の成立根拠は、三角関数の加法定理から
sin(θ + θ0) = (sinθ)cosθ0 + (cosθ)sinθ0
が言える事と、r = 1/u(∵TEC-0-1-32-1,2)である事です。2015.11.16,30
8,9行目の等号の成立根拠は、t < 0 ではθ< 0 である事(∵TEC-0-1-35-1〜14VIIのグラフと、TEC-0-1-32-1,2の式)です。
TEC-0-1-35-1〜14VIIのグラフ中の矢印が時間経過の向きを表している事、に気を付けて下さい。
TEC-0-1-36-8,9では、
θ= -|θ|,
sinθ = sin(-|θ|) = -sin|θ|,
cosθ = cos(-|θ|) = cos|θ|
という式変形を使っています。2015.11.16,29,30;2016.02.01
10,11行目の等号の成立は、TEC-0-1-34-24〜29の式です。
|θ| ≧ 0 ∴ sin|θ| ≧ 0 なので、sin|θ| = √[1 - (cos|θ|)2] です。
θ0 ≧ 0 ∴ sinθ0 ≧ 0 なので、sinθ0 = √[1 - (cosθ0)2] です。
θ0 ≧ 0 である事は、TEC-0-1-34-28,29の式と、TEC-0-1-35-15の範囲指定から、分かります。
t → -∞ が u → 0 に書き換えられているのは、t → -∞ で u → 0 だからです。
この事は、TEC-0-1-35-1〜14VIIのグラフと、TEC-0-1-32-1,2の式から、分かります。2015.11.16,29
18〜21行目の式は、14〜17行目の式に対して、
を括り出した後で、
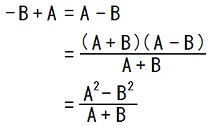
という変形を施す事によって、得られます。2015.11.29,30
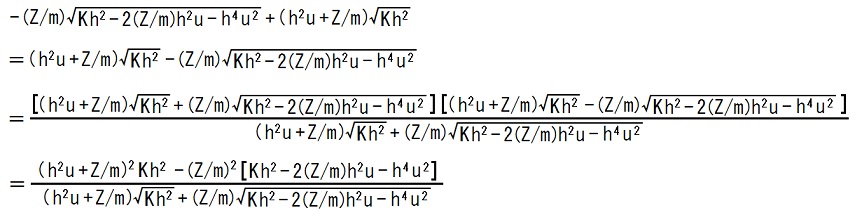
22,23行目の式は、18〜21行目の式中の u → 0 という極限操作を実行すれば、得られます。
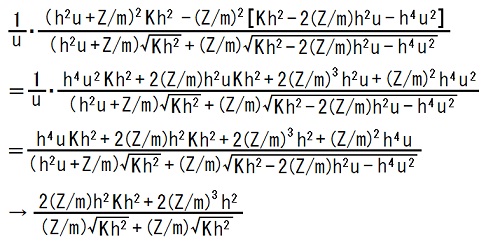
(分子)/uの極限と分母の極限が別々に存在するケースです。2015.11.29,30;2016.02.01
24,25行目の等号の成立を示す時には、h > 0である事(CAN-1-1-13-24)を使います。
h > 0だから、
√(Kh2) = h√K
が成り立ちます。2016.02.01
4〜25行目の計算の結果を、手っ取り早く得る方法が、TEC-0-1-37-19〜23に書かれています。2016.02.01
26,27行目の等号の成立根拠は、4〜25行目の計算結果です。2015.11.16
28,29行目の左の等号の成立根拠は、2,3行目の計算結果です。2015.11.16
【SEOテキスト】宇田雄一03.10.20,CAN-1-1-13-26〜30,TEC-0-1-29〜35VII,φ=π-[θ(t→+∞)-θ(t→-∞)]=π-2θ0,b=lim t→-∞ r(t)sin[θ(t)+θ0]=lim t→-∞ (sinθ)cosθ0+(cosθ)sinθ0 /u=lim t→-∞ -(sin|θ|)cosθ0+(cos|θ|)sinθ0 /u=lim t→-∞ 1/u[-√ 1-(h2u+Z/m)2/ (Z/m)2+Kh2・Z/m/√ (Z/m)2+Kh2 + h2u+Z/m /√ (Z/m)2+Kh2・√ 1- (Z/m)2/ (Z/m)2+Kh2]=lim t→-∞ 1/u[-(Z/m)√ Kh2-2(Z/m)h2u-h4u2 / (Z/m)2+Kh2 + (h2u+Z/m)√Kh2 / (Z/m)2+Kh2]=lim t→-∞ 1/u・1/ (Z/m)2+Kh2 [(h2u+Z/m)2Kh2-(Z/m)2[Kh2-2(Z/m)h2u-h4u2] / (h2u+Z/m)√Kh2+(Z/m)√ Kh2-2(Z/m)h2u-h4u2]=1/ (Z/m)2+Kh2・2h2(Z/m)Kh2+2(Z/m)3h2 / 2(Z/m)√Kh2=h/√K,db/dh=1/√K※hでの微分はKを一定に保って行なう。これはt→-∞での速さを変えずbを変化させる事に相当する。dφ/dh=-2dθ0/dh=-2d(cosθ0)/dh・dθ0/d(cosθ0)