次のページ
前のページ
目次
TEC-0-1-29
TEC-0-1-34
TEC-0-1-36
TEC-0-1-37
TEC-0-1-44
TEC-0-1-45
COM-1-17
[ 1 ] (2)
[ 1 ] (5)
[補足説明欄]
1行目の「 [2] 2体問題 (n = 2) 」は、CAN-1-1-18-2からCAN-1-1-19-29までの記事のタイトルです。
nはCAN-1-1-15-3のnです。2019.06.23
2行目の「 ① 運動方程式 (作用反作用則を仮定する[1]②) 」は、3～17行目の記事のタイトルです。2019.06.23
3行目の [実験室系] は、4,5行目の記事のタイトルです。2019.06.23
4行目のF12は、1つのベクトルを変数とするベクトル値関数(ベクトルをベクトルに写す写像)であり、ベクトルではありません。
F12(r1 - r2)は、関数F12の値であり、ベクトルです。
関数F12は、ベクトルxを、ベクトルF12(x)に、写します。2019.06.23
5行目のF21は、1つのベクトルを変数とするベクトル値関数であり、ベクトルではありません。
F21(r2 - r1)は、関数F21の値であり、ベクトルです。
関数F21は、ベクトルxを、ベクトルF21(x)に、写します。2019.06.23
4,5行目の左の等号は、CAN-1-1-15-3～14で
n = 2, Fi(x, u, w) = 0, Fik(x, y, u, v, w) = F'ik(x - y)
とした場合に相当します。
ただしF'ikは、ベクトル変数ベクトル値関数であり、本当はこの様にFikとは異なる記号で表される必要が有りますが、CAN-1-1-18では、このF'ikをFikと書いています。
Fi(x, u, w) = 0 である事は外力が存在しない事を意味しますが、この様に外力を全く受けない系は「孤立系」と呼ばれます。
ここで外力が存在しない場合を考えているのは、COM-1-13-6～11の条件設定を念頭に置いているからです。
つまり対象として全体系を考えている、世界に存在するのは2つの質点P1とP2だけで、それら以外には何も存在しない場合を考えている、従がってP1もP2も第3者から力を受ける事は全く無い、というわけです。
この理屈によって、全体系は必ず孤立系です。
また実際には正確に孤立系だと言えるのは全体系だけでしょう。
その意味で、基礎の研究においては、全体系と孤立系は実質上同義であり、孤立系は全体系を意味する隠語だとすら言えるかもしれません。
しかし孤立系の定義と全体系の定義は異なるし、近似的になら部分系を孤立系として扱う事が出来る場合も有ります。
CAN-1-1-15-19～22,27～30およびCAN-1-1-16-6～17から、全体系の全運動量、全角運動量、力学的エネルギーはいずれも時間が経っても変化しない事、が分かります。
これを運動量保存の法則(運動量保存則)、角運動量保存の法則(角運動量保存則)、エネルギー保存の法則(エネルギー保存則)と呼びます。2019.06.23,24;2019.07.14,23
5行目の右の等号は作用反作用の法則が成り立つ事を意味します。
F'ki(y - x) = - F'ik(x - y) ならば
Fik(x, y, u, v, w) = F'ik(x - y) = -F'ki(y - x) = -Fki(y, x, v, u, w) と成ってCAN-1-1-15-16の条件が成り立つからです。
ここで x, y としては任意のベクトルを考えているので、
F'ki(y - x) = - F'ik(x - y) という条件は、
F'ki(-x) = - F'ik(x) という条件と同じです。2019.06.23,24,25;2019.07.14
6行目の [質量中心系] は、6～17行目の記事のタイトルです。2019.06.23
6行目の F1 = F2 = 0 という式は、F1(t) = F2(t) = 0 という意味です。
これは外力がゼロベクトルである事を意味するので、5行目まででも仮定されています。2019.06.23,24
7行目の式は質量中心の運動方程式です。
8行目の式は質量中心系でのP1の運動方程式です。
9行目の式は質量中心系でのP2の運動方程式です。
7行目の式から質量中心の運動は等速直線運動だと分かるので、ここでの質量中心系は慣性系です。
同様の理由で、質点系Sが孤立系でSの内力が作用反作用の法則に従がうならばn≧3でも、Sの質量中心の運動は等速直線運動に成りSの質量中心系は慣性系です。2019.06.24,25
7行目の最も左の等号の成立根拠はCAN-1-1-16-24,25に書かれています。
その事はTEC-0-1-44-8で指摘されています。2019.06.24
7行目の左から2番目の等号 F1 + F2 = 0 の成立根拠は6行目の仮定 F1 = F2 = 0 です。2019.06.24
8行目の最も左の等号の成立根拠は d2r'1/dt2 = d2r1/dt2 ですが、d2r'1/dt2 = d2r1/dt2 の成立根拠はTEC-0-1-44-9,10に書かれています。2019.06.24
8行目の左から2番目の等号 m1d2r1/dt2 = F'12(r1 - r2) の成立は4行目に書かれています。2019.06.24
8行目の最も右の等号 F'12(r1 - r2) = F'12(r'1 - r'2) の成立根拠はTEC-0-1-44-17,18に書かれています。2019.06.24;2019.07.14
9行目の式
m2d2r'2/dt2 = -F'12(r'1 - r'2)
の成立根拠は、5行目の式と d2r'2/dt2 = d2r2/dt2 およびTEC-0-1-44-17,18の内容です。
d2r'2/dt2 = d2r2/dt2 の成立根拠はTEC-0-1-44-9,11に書かれています。2019.06.24;2019.07.14
10,11行目の式は質量がμで位置ベクトルが r'1 - r'2 である単一の仮想的な質点の運動方程式と同じです。
μが換算質量と呼ばれるのは、このためです。2019.06.24
10,11行目の式の導出は、TEC-0-1-44-12～16で行なわれています。2019.06.24
14～17行目の式から、r'1の向きとr'2の向きは正反対であり、|r'1| : |r'2| = m2 : m1 だと分かります。
つまり、ここでの質量中心は P1 と P2 を結ぶ線分を m2 : m1 の比に内分しています。2019.06.26;2019.07.14
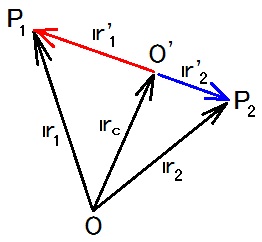2019.06.2614～17行目の式の導出は、TEC-0-1-44-23～27で行なわれています。2019.06.24
7～17行目をまとめると、こうです。
まず、与えられた関数F'12に対して10,11行目の微分方程式を解けば r'1(t) - r'2(t) と t の関係が分かります。
それを14～17行目の式に代入すれば r'1(t) と t の関係も r'2(t) と t の関係も分かります。
7行目の微分方程式を解くと、a, b を任意の定ベクトルとして rc(t) = ta + b だと分かります。
以上の結果とCAN-1-1-16-26の式ゆえに、
r1(t) = rc(t) + r'1(t) = ta + b + r'1(t), r2(t) = rc(t) + r'2(t) = ta + b + r'2(t)
という関係を通して、r1(t) と t の関係も r2(t) と t の関係も分かります。2019.06.25,26;2019.07.05
18行目の「 ② 万有引力の法則 」は、19～22行目の記事のタイトルです。2019.06.23
19～22行目で説明されている力の法則を「万有引力の法則」と呼びます。
万有引力の法則はアイザック・ニュートンによって発見されました。
ニュートンはリンゴが木から落ちるのを見て万有引力の存在に気付いた、という逸話は、その真偽の程はともかくとして、有名です。
この逸話は、どの時代(人類の総知のレベルがどれだけだった時代)にどれだけの事が出来れば世界1の天才だと言えるのか、を示す基準として重要です。
長さの基準としてメートル原器が果たして来た役割を才能や能力や業績のレベルの基準として果たす原器として使えます。
そういう原器を出来るだけ幾つも見付ける事により、それらに依拠した才能や能力や業績のレベル評価の信頼性を高める事が出来ます。
それら原器に依拠するのとは別の方法での評価は、どれも(IQテストも)、それら原器に依拠する方法よりも信頼性が低いと私は考えます。
統計値の欺瞞、個別成績の虚偽申告、カンニング等の不正工作が可能だし、そのテストで測定されるのはどういう種類の能力か、その種類の能力は本当にそのテストで測定できるのか、および、その種類の能力は本当に重要なのか、という点に疑問の余地が残るからです。
自分の業績が原器で示されている程度に傑出して当代随一であるか否か、それ以外は全て不確実です。2019.07.01,03,15,16,17
G = 6.67×10-11[m3・s-2・kg-1]
記入2019.07.05
20,21行目のFijは、1つのベクトルを変数とするベクトル値関数であり、ベクトルではありません。
Fij(ri - rj)は、関数Fijの値であり、ベクトルです。
関数Fijは、ベクトルxを、ベクトルFij(x)に、写します。
1つのベクトルを変数とするベクトル値関数F'ikを F'ik(x) = -Gmimkx/|x|3 という風に定義するならばCAN-1-1-15-8の右辺のベクトル値関数FikはF'ikを使って
Fik(x, y, u, v, w) = F'ik(x - y)
という風に定義される、という意味の事がCAN-1-1-18-20,21には書かれています。
これなら F'ki(-x) = -F'ik(x) も成り立ちます。
したがって、これはCAN-1-1-18-4,5で仮定した力の法則の特別な場合なので、n = 2ではCAN-1-1-18-18～22についてはCAN-1-1-18-2～17の一般論が全て有効です。
CAN-1-1-18-20,21ではF'ijをFijと書いています。2019.06.24;2019.07.14
20,21行目の関数F'12を10,11行目で関数F'12として採用すれば、10,11行目の式は具体的には、
μ(d/dt)2[r'1(t) - r'2(t)] = -Gm1m2[r'1(t) - r'2(t)]/|r'1(t) - r'2(t)|3
と書けます。
この微分方程式を解いて r'1(t) - r'2(t) と t の関係を求める事は、質点の力学(第2章)で
m = μ, Z = -Gm1m2
としてCAN-1-1-13-21,22の場合の r(t) と t の関係を求める事と全く同じです。
それはTEC-0-1-29からTEC-0-1-35までで行なわれています。
そこで明らかにされた r(t) と t の関係が、そのまま、CAN-1-1-18-10,11,20,21の場合の r'1(t) - r'2(t) と t の関係です。2019.06.25,26
18～22行目についての補足説明が、TEC-0-1-45-27～30に書かれています。2019.06.25
23行目の「 ③ 散乱 (逆2乗中心斥力) 」は、CAN-1-1-18-24からCAN-1-1-19-29までの記事のタイトルです。2019.06.23
CAN-1-1-18-23からCAN-1-1-19-29まででは、CAN-1-1-18-2～17に書かれている一般論を、
Z ＞ 0 and F'12(x) = F'21(x) = Zx/|x|3 ∴ F'21(-x) = -F'12(x)
である場合に、適用しています。
この場合、10,11行目の式は具体的には、
μ(d/dt)2[r'1(t) - r'2(t)] = Z[r'1(t) - r'2(t)]/|r'1(t) - r'2(t)|3
と書けます。
この微分方程式を解いて r'1(t) - r'2(t) と t の関係を求める事は、質点の力学(第2章)で m = μ, Z ＞ 0 としてCAN-1-1-13-21,22の場合の r(t) と t の関係を求める事と全く同じです。
それはTEC-0-1-29からTEC-0-1-35までで、場合VIIとして、行なわれています。
そこで明らかにされた r(t) と t の関係が、そのまま、 CAN-1-1-18-23からCAN-1-1-19-29まででの r'1(t) - r'2(t) と t の関係です。
以上の議論は、n = 2 の場合の CAN-1-1-18-18～22 についての議論とほぼ同じですが、CAN-1-1-18-18～22 では Z ＜ 0 の場合を考えたのに対して、CAN-1-1-18-23からCAN-1-1-19-29まででは Z ＞ 0 の場合を考える点と散乱角まで計算する点が、違っています。2019.06.26,28
24行目では、実験室系での入射速度がvであり衝突径数がbである場合を考える、と宣言されています。
これは、t → -∞ で dr2(t)/dt → 0, |dr1(t)/dt| → v, [P1の軌道の漸近線(直線)とP2の距離] → b、である場合を考える、という意味です。
「速度」は速度ベクトルを意味し、速度ベクトルの大きさは「速さ」と呼ばれる、vは速度ベクトルではなく速さなので、本当はvを「入射速度」ではなく「入射速さ」と呼ぶべきですが、入射速度と呼ぶのが慣例の様です。2019.06.26;2019.07.14
25行目に書かれている様に r'1 - r'2 の(入射速度, 衝突径数)も(v, b)である事は、
r'1(t) - r'2(t) = r1(t) - r2(t) ∵ TEC-0-1-44-17
から分かります。
r'1 - r'2 の入射速度がvであるとは、t → -∞ で | (d/dt)[r'1(t) - r'2(t)] | → v である事を言います。
しかし、これは成り立っています。なぜならば、
limt→-∞| (d/dt)[r'1(t) - r'2(t)] |
= limt→-∞| (d/dt)[r1(t) - r2(t)] |
= limt→-∞| dr1(t)/dt - dr2(t)/dt |
= limt→-∞| dr1(t)/dt - 0 |
= limt→-∞|dr1(t)/dt|
= v
だからです。
r'1 - r'2 の衝突径数がbであるとは、r'1 - r'2 (を位置ベクトルとする動点の軌道)の漸近線(直線)と原点(ゼロベクトルを位置ベクトルとする点)の距離がbである事を言います。
これも成り立っています。
[ (r'1 - r'2)の漸近線 ] = [ (r1 - r2)の漸近線 ] = 「 [r1 - limt→-∞r2(t)]の漸近線 」
この漸近線と原点の距離は、「r1 の漸近線」と「limt→-∞r2(t) を位置ベクトルとする点」の距離に等しく、それは b だと仮定されているからです。
ただし、t → -∞ で dr2(t)/dt → 0 だからと言って t → -∞ で r2(t) が収束するとは限りません。
もし t → -∞ で r2(t) が収束しないならば、[ (r1 - r2)の漸近線 ] と原点の距離をbの定義だと考えて下さい。
t → -∞ で r2(t) が収束するか否かを私は知らないし、この点が議論されているのを私が見た事は1回も有りません。2019.06.26,28;2019.07.05,06,14
26行目の「r'1 - r'2 の散乱角φ'」とは、r'1 - r'2 (を位置ベクトルとする動点の軌道)の t → -∞ での漸近線(直線)と t → +∞ での漸近線(直線)の為す角の事です。2019.06.28
27行目に書かれている様にTEC-0-1-36-2,3の式を使う理由は、この式がCAN-1-1-13-27の式に相当するからです。2019.06.28
28,29行目には、TEC-0-1-34-28,29の式中のK, hの値としては K = v2, h = vb を使え、という指示および、その根拠はTEC-0-1-29-13,14とTEC-0-1-37-20の記述である事が、書かれています。
ですが「根拠はTEC-0-1-37-20,21の内容だ」と書くべきでした。
TEC-0-1-29-13,14の式はTEC-0-1-37-20で根拠として引用されているからです。
K, h の値は、これとは別に、
b = h/ √K ∵ TEC-0-1-36-4～25
r2dθ/dt = h ∵ CAN-1-1-13-23
r2dθ/dt = |r × v| ∵ CAN-1-1-3-15～24
これらを根拠にして算出する事もできます。
衝突径数と入射速度の定義から |r × v| = vb である事が分かります。
これを代入すると、
h = r2dθ/dt = |r × v| = vb,
b = h/ √K = vb/√K ∴ K = v2.
2019.06.26,28
COM-1-13-23～26への補足説明の論法を n = 2 の場合に適用する事により、2体問題においてもP1の力学(P1の運動が従がう法則)を考える事が出来ます。
特に例えば n = 2 でCAN-1-1-18-18～22の場合、m2 が m1 よりもずっと大きいならばP2の運動は近似的に等速直線運動です。
質量中心の運動は等速直線運動(CAN-1-1-18-7)であり、P2の速度は近似的に質量中心の速度に等しくなる(CAN-1-1-18-14～17への補足説明)からです。
そこで r2(t) = ta + b として、これをCAN-1-1-18-4の式に代入すると、
m1d2r1(t)/dt2 = -Gm1m2[r1(t) - (ta + b)]/|r1(t) - (ta + b)|3 ・・・ (1)
これは力の法則(COM-1-5-11,12)が
F(t, r, v) = -Gm1m2[r - (ta + b)]/|r - (ta + b)|3 ・・・ (2)
であり質量が m = m1 である場合の運動方程式(CAN-1-1-4-6)にP1の運動が従がう事を意味しています。
COM-1-12-7の「質点系の力学(第3章)を学べば分かる」というのは、この事です。
原因である力の法則 F'12, F'21 には時間依存性が有りません。
つまり、F'12(x, y, u, v, w) も F'21(x, y, u, v, w) も w に依存しません。
(2)の t 依存性は質点系の力学の問題を解いた結果です。
ついでの話ですが、(1)は「重力カタパルト(swing-by)」と呼ばれる人工衛星加速技術の本質を表しています。
例えば a = v0i の場合に、P2(ta + b を位置ベクトルとする点)を原点とする座標系(慣性系)で、
t → -∞ では (P1の速度ベクトル) = dr'1(t)/dt → vj
t → +∞ では (P1の速度ベクトル) = dr'1(t)/dt → vi
である様な解が(1)の解の中には存在します。
さて、この解を実験室系で見てみると、実験室系では、
t → -∞ では (P1の速度ベクトル) = dr1(t)/dt → v0i + vj
t → +∞ では (P1の速度ベクトル) = dr1(t)/dt → v0i + vi = (v0 + v)i
だから、実験室系では、
t → -∞ では (P1の速さ) = |dr1(t)/dt| → |v0i + vj| = √[(v0)2 + v2]
t → +∞ では (P1の速さ) = |dr1(t)/dt| → |(v0 + v)i| = v0 + v = √[(v0 + v)2] = √[(v0)2 + v2 + 2v0v]
と成りP1の速さが増加する事が分かります。
これは、P1がP2から受ける引力によって加速された事を意味します。2019.07.01,05;2019.07.14
【SEOテキスト】宇田雄一,04.1.9,第3章,質点系の力学,[2]2体問題(n=2),①運動方程式(作用反作用を仮定する[1]②),[実験室系],m1,1=F12(r1-r2),m2,2=F21(r2-r1)=-F12(r1-r2),[質量中心系]→[1]⑤,F1=F2=0と仮定する。,M,c=F1+F2=0∴,c=0,{,m1,'1=m1,1=F12(r1-r2)=F12(r'1-r'2),m2,'2=-F12(r'1-r'2),∴μ,d2(r'1-r'2),-,dt2,=F12(r'1-r'2),ただし,1,-,μ,≡,1,-,m1,+,1,-,m2,(μを換算質量と呼ぶ。,{,r'1=,m2,-,m1+m2,(r'1-r'2),r'2=-,m1,-,m1+m2,(r'1-r'2),②万有引力の法則,n=2の場合だけでなくn≧3の場合にも、,Fij(ri-rj)=-Gmimj,ri-rj,-,|ri-rj|3,ただし、Gは万有引力定数と呼ばれる定数だ。,③散乱(逆2乗中心斥力),実験質系での入射速度をv,衝突径数をbとするとr'1-r'2の入射速度はv,衝突径数はbだから、r'1-r'2の散乱角φ'はTEC-0-1-34-28,29のmをμに書き換え、TEC-0-1-36-2,3を適用したφに等しい。K'=v2=K(TEC-0-1-29-13,14)およびh'=vb=h(TEC-0-1-37-20)参照。