次のページ
前のページ
目次
TEC-0-1-45
[補足説明欄]
このページの内容は全てCAN-1-1-18-24〜29の記事の続きです。2019.06.29
1,2行目のφ' はCAN-1-1-18-26の散乱角φ' です。
CAN-1-1-19-1,2の cos-1 の値域は { θ | 0 ≦ θ ≦ π } です。
その事はTEC-0-1-35-15に書かれています。
CAN-1-1-19-1,2の式の成立根拠は、CAN-1-1-18-23〜29および、それへの補足説明に、書かれています。2019.06.29;2019.07.03
sinφ'の値とcosφ'の値は以下の計算で分かります。
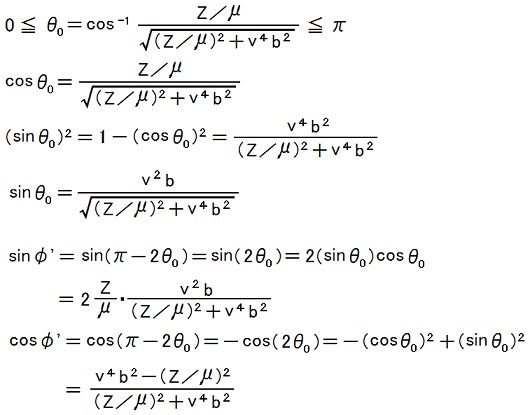
この計算の本質はTEC-0-1-37-9〜14に既出です。2019.07.02,03
4〜11行目の図では、t → +∞ でのr'1の漸近線とr'2の漸近線は同一である事に成っていますが、これは誤りです。
t → -∞ での2つの漸近線の間隔がbならばt → +∞ での2つの漸近線の間隔もbです。2019.06.29,30
12,13行目の内容の根拠は以下です。
まず、CAN-1-1-18-14〜17の式から、
r'2(t) = -(m1/m2)r'1(t) ・・・ (1)
これをtで微分する事によって、
dr'2(t)/dt = -(m1/m2)dr'1(t)/dt
∴ |dr'2(t)/dt| = (m1/m2)|dr'1(t)/dt| ・・・ (2)
また(1)によって、
| (d/dt)[r'1(t) - r'2(t)] | = | (d/dt)[r'1(t) + (m1/m2)r'1(t)] | = [1 + (m1/m2)]|dr'1(t)/dt| ・・・ (3)
だと分かります。
また、CAN-1-1-18-25に書かれている様に t → -∞ で | (d/dt)[r'1(t) - r'2(t)] | → v だとすると、
t → -∞ でだけでなく t → +∞ でも | (d/dt)[r'1(t) - r'2(t)] | → v です。
その理由は、TEC-0-1-29〜TEC-0-1-35の場合VIIにおいては |t| が同じなら t ＜ 0 と t ＞ 0 で (r, |θ|) が同じだからCAN-1-1-2-16のベクトルvの大きさ
√[(dr/dt)2 + (rdθ/dt)2] = √[(dr/dt)2 + r2(dθ/dt)2] = √[(dr/dt)2 + r2(d|θ|/dt)2]
も同じに成るからです。
t → ±∞ で | (d/dt)[r'1(t) - r'2(t)] | → v ・・・ (4)
(3)(4)によって、
t → ±∞ では [1 + (m1/m2)]|dr'1(t)/dt| → v ∴ |dr'1(t)/dt| → [m2/(m1 + m2)]v ・・・ (5)
(5)(2)によって、
t → ±∞ では |dr'2(t)/dt| → [m1/(m1 + m2)]v
だと分かります。2019.06.29,30
16,17行目のφはr1の t → -∞ での漸近線と t → +∞ での漸近線の為す角です。
その事が、22〜29行目の図の中で図示されています。2019.06.29
15〜20行目の式の導出は、TEC-0-1-45-2〜24で行なわれています。2019.06.29
上で算出されたsinφ'の値とcosφ'の値およびCAN-1-1-18-12,13の式で定まるμの値をCAN-1-1-19-19,20に代入する事によってtanφの値を知る事が出来ます。
その計算は以下です。2019.07.02,03
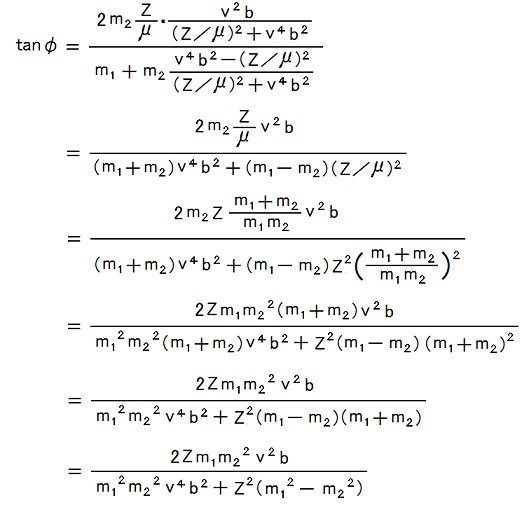2019.07.03,04P1がアルファ粒子(ヘリウムの原子核)で、P2が金の原子核である場合には、CAN-1-1-18-23からここまでで考えた散乱は「ラザフォード散乱」と呼ばれます。
この場合、
m1 ≒ 6.64×10-27[kg], m2 ≒ 3.27×10-25[kg],
Z = 9.0×109[kg・m3・s-4・A-2]×(P1の電荷)×(P2の電荷) ・・・ クーロンの法則
≒ 9.0×109[kg・m3・s-4・A-2]×3.20×10-19[A・s]×1.27×10-17[A・s]
＝ 9.0×109×3.20×10-19×1.27×10-17[kg・m3・s-2]
≒ 3.66×10-26[kg・m3・s-2]
です。
ここでのZの値の算出根拠は「クーロンの法則」と呼ばれます。
クーロンの法則は現象論的な法則であり、電磁気学正典第4章[1](2)で解説されています。
ラザフォード散乱の実験では、数原子にまで薄くした金箔に垂直にアルファ線(高速のアルファ粒子)を照射したそうです。
極めて薄い金箔を使った理由は、おそらく、1個のアルファ粒子につき散乱が複数回繰り返されるのを防ぐ為でしょう。
金箔の厚さ、金箔内の単位体積に存在する金の原子核の個数、およびアルファ粒子の入射速度vが分かれば、上で明らかにしたtanφの式を使って、散乱角がφに成る確率密度P(φ)を計算する事が出来ます。
(α＜φ＜βと成る確率) = ∫αβ dφ P(φ)
この計算結果が実験結果と良く一致したのでしょう、ラザフォード散乱の実験結果は原子核が原子のサイズに比して点と見なせるぐらいに小さい証拠だ、と言われます。
(アルファ粒子のエネルギー) = (1/2)m1v2
だから、vの値はアルファ粒子のエネルギーから求める事が出来ます。
理論値と実験値の一致を理由にするのでなく、単に実験でφが非常に大きい事も有ったという理由だけで、原子核が原子のサイズに比して点と見なせるぐらいに小さいと結論付ける、のは間違いです。
なぜならアルファ粒子と金の原子核がビリヤードにおける様な衝突をしたかもしれないからです。
それなのに、ラザフォード散乱の実験でφが非常に大きい事も有ったので原子核は原子のサイズに比して点と見なせるぐらいに小さいと分かった、という説明の仕方を私は何度も目に(耳に)しました。
これは解説の伝統の轍のひとつと言えるでしょう。
ただし2019年07月15日に本項を書き終えるよりも何年も前に私は本項を書き始めたので、その影響で2019年07月15日時点では既に解説の伝統に変化が生じている可能性が有ります。
ビリヤードにおける様な衝突ではない、という事は、散乱ではあるけど衝突ではない、という事です。
衝突径数って言うけどね。
ラザフォード散乱の問題は、量子力学でも計算し直してみる必要が有ります。
それは量子力学正典第3章§3-1[2](4)で行なわれています。2019.07.04,05,15
【SEOテキスト】04.1.9,宇田雄一,第3章,質点系の力学,φ'=π-2cos-1[,Z/μ,-,√,(Z/μ)2+v4b2,],質量中心系で見た図は、,1,φ',r'1,b,r'2,2,t→±∞では,|,'1|→,m2,-,m1+m2,v,|,'2|→,m1,-,m1+m2,v,実験室系で見ると、,tanφ=,m2,-,m1+m2,v sinφ',-,m1v,-,m1+m2,+,m2,-,m1+m2,v cosφ',=,m2 sinφ',-,m1+m2 cosφ',φ,1,b,2