次のページ
前のページ
目次
TEC-0-1-40
TEC-0-1-41
TEC-0-1-43
COM-1-16
【補足説明欄】
1行目の「④内力が保存力である場合の質点系のエネルギー」は、2～17行目の記事のタイトルです。2016.05.04
2行目の Fik は、CAN-1-1-15-8 の式の右辺の Fik です。2016.05.04
2行目の∇i は、TEC-0-1-43補足説明欄赤枠内(13)で定義されている ∇i ではなく、
∇i ≡ i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)
という風に定義される ∇i です。(CAN-1-1-5-18,19への補足説明中の∇と見比べて下さい)
つまり、CAN-1-1-16-2の式の右辺を解釈するに当たっては、
ri = xii + yij + zik
rk = xki + ykj + zkk
だとし、
∇iUik(ri, rk)
= [i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][Uik(ri, rk)] ∵TEC-0-1-43補足説明欄赤枠内(16b)(17)
という風に読みます。
だから、CAN-1-1-16-2の式は、
Fik(ri, rk, vi, vk, t) = -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][Uik(ri, rk)] ・・・(1)
という意味です。[右辺の意味はTEC-0-1-40補足説明欄赤枠内(26)で説明されています]
これは Fik という関数と Uik という関数の関係を表す式であり、変数は何でも良いので、
Fik(x, y, u, v, w) = -[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][Uik(x, y)] ・・・(2a)
と書いても意味は変わりません。
(2a)とTEC-0-1-43補足説明欄赤枠内(16a)から、
Fik(x, y, u, v, w) = -∇x[Uik(x, y)] ・・・(2)
と書いても意味は変わらない事、が分かります。
TEC-0-1-43補足説明欄赤枠内(13)で定義されている ∇k を使えば、同じ事を、
Fik(x, y, u, v, w) = -(∇1Uik)(x, y) ・・・(3)
という風にも書けます。
その根拠は、TEC-0-1-43補足説明欄赤枠内(14a)(16a)です。2016.05.04,06,13,17,18,21,23
2行目の式で表されている条件は、Fik(ri, rk, vi, vk, t) が vi, vk, t に依存しない事、つまり
Fik(x, y, u, v, w) = F'ik(x, y)
である様な関数 F'ik が存在する事を、必要条件として含んでいます。2016.05.04,07,13
2～4行目の条件について、TEC-0-1-43の2～6行目と9～19行目に、補足説明が書かれています。2016.05.07,11
3行目の「Uik(ri, rk) = Uki(rk, ri) が恒等式に成る」という条件は、Uik という関数と Uki という関数の間に
Uik(x, y) = Uki(y, x)
という関係が存在する事、を主張する物です。2016.05.04,17
4,5,16,17,20,23行目の S は、CAN-1-1-15-3 の S です。2016.05.04
2～5行目に書かれている保存力の定義を、CAN-1-1-5-17～20に書かれている定理と見比べて下さい。2016.05.04
4,5行目について。
質点系の内力は必ず保存力だ、という法則は存在しません。
ゴム塊の様な弾性体の内力は保存力ですが、粘土塊の様な塑性体の内力は非保存力です。2016.05.07,08
6行目の Fi は、CAN-1-1-15-7 の式の右辺の Fi です。2016.05.04
6行目の∇を私は、TEC-0-1-43補足説明欄赤枠内(8)で定義されている∇ではなく、CAN-1-1-5-18,19への補足説明中の∇のつもりで書いています。
したがって、CAN-1-1-16-6の式は、
Fi(r, v, t) = -[i(∂/∂x) + j(∂/∂y) + k(∂/∂z)][Vi(r)] + fi(r, v, t) ・・・(1)
という意味です。(r = xi + yj + zk)
TEC-0-1-43補足説明欄赤枠内(8)で定義されている∇を使って
Fi(r, v, t) = -(∇Vi)(r) + fi(r, v, t) ・・・(2)
という風に書いても論理的内容は(1)と同じである事が、TEC-0-1-43補足説明欄赤枠内の(9a)と※1から分かります。
(2)は、Fi という関数と Vi という関数と fi という関数の関係を表す式なので、変数としては何を用いても良く、
Fi(x, y, w) = -(∇Vi)(x) + fi(x, y, w) ・・・(2a)
と書いても、
Fi(ri, vi, t) = -(∇Vi)(ri) + fi(ri, vi, t) ・・・(2b)
と書いても、論理的な内容は変わりません。[∇としてはTEC-0-1-43補足説明欄赤枠内(8)の∇を用いる]
(2b)と同じ事を
Fi(ri, vi, t) = -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][Vi(ri)] + fi(ri, vi, t) ・・・(3)
という式で表す事も出来る事が、TEC-0-1-43補足説明欄赤枠内の(9a)と※1から、分かります。
CAN-1-1-5-18,19への補足説明に書かれている∇を使って
Fi(ri, vi, t) = -∇Vi(ri) + fi(ri, vi, t)
と書いたのでは、
Fi(ri, vi, t) = -[i(∂/∂x) + j(∂/∂y) + k(∂/∂z)][Vi(ri)] + fi(ri, vi, t)
という意味に成ってしまい、これでは、論理的内容が(3)と食い違ってしまい、従って(1)とも食い違ってしまいます。
CAN-1-1-16-6の式で私が変数として r を用い ri を用いなかったのは、そのためです。2016.05.04,17,18,21,23,24
7行目の n は、CAN-1-1-15-3 の n です。2016.05.04
6,7行目の内容について、COM-1-16-17,18に補足説明が書かれています。2016.05.07
9～12行目の式の導出は、TEC-0-1-40-27～TEC-0-1-41-16で、行なわれています。2016.05.04
9～12行目の式を、TEC-0-1-8-25～27の計算の結果やCAN-1-1-5-29～CAN-1-1-6-2に書かれている法則と、見比べて下さい。2016.05.07,18
14,15行目の式中の Uik の和
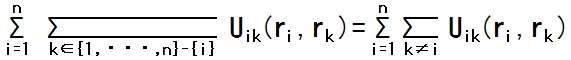
は、{1, ・・・, n} から2つ取り出す全ての順列(i, k)に渡っての和です。
この事と Uik(ri, rk) = Uki(rk, ri) である事(3行目の式)から、この和は {1, ・・・, n} から2つ取り出す全ての組合せ(i, k)に渡っての和
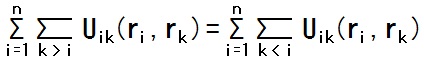
の2倍だ、と分かります。
したがって、その1/2倍である
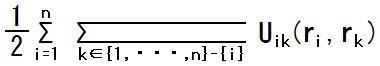
は、{1, ・・・, n} から2つ取り出す全ての組合せ(i, k)に渡っての Uik の和に等しく、これは「内力のポテンシャルエネルギー」と呼ばれます。
例えば n = 3 の場合には、
という風に成ります。2016.05.04,06,18
2～7行目の条件が成り立つ場合、14,15行目の定義を採用すれば、Pi に働く力は、
Σk≠iFik(t) + Fi(t) = -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][U(r1, ・・・, rn)] + fi(ri, dri/dt, t) ・・・(1)
という風に表されます。(ri = xii + yij + zik)
その理由は以下です。[∇i ≡ i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)]
i = j or i = k でなければ ∇i[Ujk(rj, rk)] = 0 だし、
Σj=1nΣk≠j Ujk(rj, rk) の中に Uii(ri, ri) という項は含まれていないから、
∇iΣj=1nΣk≠j Ujk(rj, rk)
= Σj=1nΣk≠j ∇i[Ujk(rj, rk)] ∵COM-1-16補足説明欄赤枠内(3a)
= Σk≠i ∇i[Uik(ri, rk)] ・・・ j = i の項
+ Σj≠i ∇i[Uji(rj, ri)] ・・・ k = i の項
∴ -∇i[U(r1, ・・・, rn)]
= -∇i[(1/2)Σj=1nΣk≠j Ujk(rj, rk) + Σj=1nVj(rj)] ∵CAN-1-1-16-14,15
= -(1/2)∇iΣj=1nΣk≠jUjk(rj, rk) - Σj=1n∇i[Vj(rj)] ∵COM-1-16補足説明欄赤枠内(3)
= -(1/2){Σk≠i∇i[Uik(ri, rk)] + Σj≠i∇i[Uji(rj, ri)]} - Σj=1n∇i[Vj(rj)]
= -(1/2){Σk≠i∇i[Uik(ri, rk)] + Σj≠i∇i[Uij(ri, rj)]} ∵CAN-1-1-16-3
-∇i[Vi(ri)] ∵ j ≠ i ⇒ ∇iVj(rj) = 0
= -(1/2){2Σk≠i∇i[Uik(ri, rk)]} -∇i[Vi(ri)]
= Σk≠i{-∇i[Uik(ri, rk)]} - ∇i[Vi(ri)]
= Σk≠iFik(ri, rk, dri/dt, drk/dt, t) - ∇i[Vi(ri)] ∵CAN-1-1-16-2の補足説明の(1)
∴ -∇i[U(r1, ・・・, rn)] + fi(ri, dri/dt, t)
= Σk≠iFik(ri, rk, dri/dt, drk/dt, t) - ∇i[Vi(ri)] + fi(ri, dri/dt, t)
= Σk≠iFik(ri, rk, dri/dt, drk/dt, t) + Fi(ri, dri/dt, t) ∵CAN-1-1-16-6の補足説明の(3)
= Σk≠iFik(t) + Fi(t) ∵CAN-1-1-15-7,8
(1)とTEC-0-1-43補足説明欄赤枠内(14a)から、TEC-0-1-43補足説明欄赤枠内(13)で定義される ∇i を使っても、
Σk≠iFik(t) + Fi(t) = -(∇iU)(r1(t), ・・・, rn(t)) + fi(ri(t), dri(t)/dt, t) ・・・(2)
が成り立つ、と分かります。
(1)および、その証明においては、ri(t)をriと、dri(t)/dtをdri/dtと略記しています。
これは、略記しなければ、例えば(1)中の∂/∂xiを定義が不明な∂/∂xi(t)に書き換えるなどする必要が生じてしまうからです。
略記しても、式中に定義が不明な∂/∂xi(t)等が含まれる事は気付かれ難く成るだけで変わりません。
この事は(1)の欠点です。
(1)にはこの欠点が有るので、正式な表現は(2)であり(1)は(2)の崩し書きに過ぎない、と考えるべきです。
しかし、微分を実行した後でriにri(t)を代入する、と考えれば(1)もその証明も間違っていません。2016.05.04,06,07,08,09,17,18,21,24;2019.06.08
9,10,16,17行目で定義されている質点系の力学的エネルギーを、CAN-1-1-6-1の質点の力学的エネルギーと見比べて下さい。2016.05.04
18行目の「⑤質量中心」は、CAN-1-1-16-19からCAN-1-1-17-11までの記事のタイトルです。2016.05.04
19行目の[質量中心の運動]は、20～25行目の記事のタイトルです。2016.05.04
質量中心と重心では定義が異なります。
質量中心は(慣性)質量に着目した概念であるのに対して、重心は受ける重力(万有引力)に着目した概念です。
力学を学んでいない人は質量中心という言葉を知らないし、重力場が一様ならば質量中心と重心は一致するので、私も日常会話では質量中心を重心と言い換えます。
大抵の人は力学を学んでいないので、質量中心と言ったのでは話が通じないからです。
しかし、そんな時の私は心の中で「本当は重心じゃなくて質量中心なんだけどなあ」と思っています。2019.06.17,18,19
24,25行目の式を、CAN-1-1-4-6の式にCAN-1-1-1-8,9のαを代入して得られる式と、比較して下さい。
そうすれば、CAN-1-1-16-24,25の式は質量がMで位置ベクトルがrcである単一の質点の運動方程式と同じだ、と分かります。
ただし、CAN-1-1-16-24,25の式では右辺は外力のみの合力であり内力が全く現れない事、に気を付けて下さい。2019.06.18
24,25行目の式の導出は、TEC-0-1-41-18,19で、行なわれています。2019.06.17
26行目の[質量中心系]は、CAN-1-1-16-26からCAN-1-1-17-11までの記事のタイトルです。2016.05.04
質量中心系は質量中心を原点とする座標系です。
r'iは質量中心系での質点Piの位置ベクトルです。
Piの位置ベクトルをriだとする元の座標系は実験室系と呼ばれます。
「質量中心系」は「実験室系」の反対語です。2019.06.17
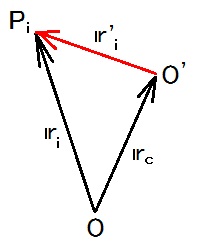2019.06.1827行目の「(a)運動量」は、28,29行目の記事のタイトルです。2016.05.04
28,29行目の左の式は、質量中心系ではSの全運動量が0である事、を表しています。
midr'i/dtは質量中心系でのPiの運動量(CAN-1-1-4-17～21; CAN-1-1-1-6,7)だからです。2019.06.17
28,29行目の右の式は、実験室系でのSの全運動量は全質量が質量中心に局在(集中)している場合と同じである事、を表しています。2019.06.17,19
28,29行目の式の導出は、TEC-0-1-41-22～27で、行なわれています。2019.06.17
脚注の「TEC-0-1-40～41，43」は「TEC-0-1-40，41，43」と同じ意味です。
【SEOテキスト】宇田雄一,03.12.13,第3章,質点系の力学,④内力が保存力である場合の質点系のエネルギー,Fik(ri,rk,vi,vk,t)=-∇iUik(ri,rk)およびUik(ri,rk)=Uki(rk,ri)が恒等式となるようなUikが全てのi≠kに渡って存在する場合、Sの内力は保存力であると言われる。Sの内力が保存力であり、かつFi(r,v,t)=-∇Vi((r)+fi(r,v,t)が恒等式となる様なV1,V2,・・・,Vnが存在する場合、次式が成り立つ。,d,-,dt,[n,∑,i=1,1,-,2,mi|,i(t)|2+U(r1(t),・・・・・,rn(t))]=,n,∑,i=1,i(t)・fi(ri(t),i(t),t),ただし、,U(r1,・・・,rn)≡,n,∑,i=1,[,1,-,2,∑,k∈{1,・・・,n}-{i},Uik(ri,rk)+Vi(ri)],と定義し、これをSのポテンシャルエネルギーと呼ぶ。9,10行目の[ ]内をSの力学的エネルギーと呼ぶ。,⑤質量中心,[質量中心の運動],位置ベクトルがrcである点をSの質量中心と呼ぶ。ただし、,rc≡,1,-,M,n,∑,i=1,mi ri,M≡∑,n,i=1,mi,Sの内力が作用反作用の法則に従う場合、次式が成り立つ。,M,d2,-,dt2,rc(t)=∑,n,i=1,Fi(t),[質量中心系]r'i≡ri-rc,(a)運動量,n,∑,i=1,mi,dr'i,-,dt,=0,n,∑,i=1,mi,i=M,c