TEC-0-1-43
ホーム ＞ 物理学正典 ＞ 初等力学正典 ＞ TEC-0-1-43
		次のページ   前のページ   目次
		CAN-1-1-15   CAN-1-1-16   COM-1-16
▲このページの上端へ行く
【補足説明欄】 「関数」と「関数の値」を区別する書き方(CAN-1-1-15-7,8に対する補足説明)では、「関数の微分」と「関数の値の微分」も区別されます。 y = f(x) を x で微分する、と考える考え方は、関数の値を微分する、と考える考え方です。 この考え方を表す記号が、普通に用いられている dy/dx や (d/dx)f(x) です。 この様に考え書く時には、f を微分するのではなく f(x) を微分する、と考えているので、 (d/dx)f(x) = (d/dx)[f(x)] ・・・(1) であって、 (d/dx)f(x) = [(d/dx)f](x) ではありません。 これに対して、 f'(x) = (d/dx)[f(x)] である様な関数 f' を考え、f を微分すると f' に成る、という風に考えるのが、関数を微分する、と考える考え方です。 この考え方を式で表すと、 f' = Df あるいは f' = D(f) という書き方に成ります。 D という写像が f を f' に写す、という風に考え書くわけです。 Df の x での値は f' の x での値だから、 (Df)(x) = (d/dx)[f(x)] ・・・(2) です。 D は関数を関数に写す写像であり、f(x) は関数ではないので、D[f(x)] という物は存在しません。 だから、(Df)(x) を Df(x) と略記しても誤解は生じないので、そうします。 Df(x) ≡ (Df)(x) ・・・(2a) これが、関数の微分の考え方と書き方です。 偏微分についても、同様の考え方と書き方が出来ます。 関数の値を微分する、と考える書き方は、 (∂/∂y)f(x, y, z) = (∂/∂y)[f(x, y, z)] ・・・(3) などです。 これに対して、関数を微分する、と考える書き方は、 ∂2f(x, y, z) = (∂2f)(x, y, z) ・・・(4) などです。 両者の関係は、以下のごとくです。 (∂1f)(x, y, z) = (∂/∂x)[f(x, y, z)] ・・・(5) (∂2f)(x, y, z) = (∂/∂y)[f(x, y, z)] ・・・(6) (∂3f)(x, y, z) = (∂/∂z)[f(x, y, z)] ・・・(7) 関数を微分すると考える書き方では、どの文字で微分するか、ではなく、何番目の変数で微分するか、を考えます。 (∂1f)(y, z, x) = (∂/∂y)[f(y, z, x)] (∂2f)(x, z, y) = (∂/∂z)[f(x, z, y)] (∂3f)(y, y, x) = (∂/∂x)[f(y, y, x)] 関数の値を微分する書き方で ∂2f(x, x, x) = (∂2f)(x, x, x) を表そうとすると、 (∂/∂y)[f(x, y, z)] を計算した結果に y = x, z = x を代入した物、 という冗長な書き方に成ってしまい不便です。 当典以外では ∂k≡∂/∂xk という記号法が用いられる事が多いけれど、当典では、そういう記号法を用いない事にします。 考え方については以上ですが、後の便の為に、以下で、記号法を幾つか作っておきます。 今まで(CAN-1-1-5-18,19への補足説明以来)は、 ∇≡i∂/∂x + j∂/∂y + k∂/∂z だとして話を進めて来ました。 これは、関数の値を微分する、と考える書き方です。 ここ以降の補足説明欄では、∇という記号は、関数の微分に用い、関数の値の微分には用いない事にします。 ここ以降の補足説明欄では、∇の定義としては、 ∇ ≡ i∂1 + j∂2 + k∂3 ・・・(8) を採用する事にします。(i, j, k は CAN-1-1-1-11〜16 の3つの単位ベクトルです) この定義式の右辺の意味は、TEC-0-1-40の補足説明欄の赤枠内の(9)と(19)から、分かります。 ∇は関数をベクトル値関数に写す写像であり、f を3変数関数とすると、∇f は3変数ベクトル値関数であり、(∇f)(x, y, z) はベクトルです。 (∇f)(x, y, z) 　= [(i∂1 + j∂2 + k∂3)f](x, y, z)　∵(8) 　= [i(∂1f) + j(∂2f) + k(∂3f)](x, y, z)　∵TEC-0-1-40補足説明欄赤枠内(19) 　= [(∂1f)(x, y, z)]i + [(∂2f)(x, y, z)]j + [(∂3f)(x, y, z)]k　　∵TEC-0-1-40補足説明欄赤枠内(9) 　= {(∂/∂x)[f(x, y, z)]}i + {(∂/∂y)[f(x, y, z)]}j + {(∂/∂z)[f(x, y, z)]}k ∴ (∇f)(x, y, z) = {(∂/∂x)[f(x, y, z)]}i + {(∂/∂y)[f(x, y, z)]}j + {(∂/∂z)[f(x, y, z)]}k ・・・(9) f(x, y, z) は、実数や複素数であり、∇の変域の元ではないので、∇[f(x, y, z)] という物は存在しません。 したがって、(∇f)(x, y, z) を ∇f(x, y, z) と略記しても誤解は生じないので、そうします。 ∇f(x, y, z) = (∇f)(x, y, z) ・・・(10) (9)とTEC-0-1-40補足説明欄赤枠内(26)から、 (∇f)(x, y, z) = [i(∂/∂x) + j(∂/∂y) + k(∂/∂z)][f(x, y, z)] ・・・(9a) だと分かります。 ベクトルを変数とする関数に対しては、 f'(xi + yj + zk) = f(x, y, z) ⇒ (∇f')(xi + yj + zk) = (∇f)(x, y, z) ・・・(11) という条件によって ∇f' を定義します。 ∇[f'(r)] という物は存在しないので、(∇f')(r) を ∇f'(r) と略記する事にします。 ∇f'(r) = (∇f')(r) ・・・(12) また、f'(xi + yj + zk) = f(x, y, z) である場合には、f' と f を区別しない事にします。(※1) 複数のベクトルを変数とする関数に対しては、 ri = xii + yij + zik ⇒ f'(r1, r2, ・・・, rn) = f(x1, y1, z1; x2, y2, z2; ・・・; xn, yn, zn) ・・・(13a) ならば、 ri = xii + yij + zik ⇒ (∇kf')(r1, r2, ・・・, rn) = [(i∂3k-2 + j∂3k-1 + k∂3k)f](x1, y1, z1; x2, y2, z2; ・・・; xn, yn, zn) ・・・(13) という条件で、∇k を定義しておきます。 i∂3k-2 + j∂3k-1 + k∂3k の意味も、TEC-0-1-40の補足説明欄の赤枠内の(9)と(19)から、分かります。 ∇k は関数をベクトル値関数に写す写像であり、f' がn個のベクトルを変数とする関数である時、∇kf' はn個のベクトルを変数とするベクトル値関数であり、(∇kf')(r1, ・・・, rn) はベクトルです。 (∇kf')(r1, ・・・, rn) 　= [(i∂3k-2 + j∂3k-1 + k∂3k)f](x1, y1, z1; ・・・; xn, yn, zn)　∵(13) 　= [i(∂3k-2f) + j(∂3k-1f) + k(∂3kf)](x1, y1, z1; ・・・; xn, yn, zn)　∵TEC-0-1-40補足説明欄赤枠内(19) 　= [(∂3k-2f)(x1, y1, z1; ・・・; xn, yn, zn)]i 　　　+ [(∂3k-1f)(x1, y1, z1; ・・・; xn, yn, zn)]j 　　　　+ [(∂3kf)(x1, y1, z1; ・・・; xn, yn, zn)]k　∵TEC-0-1-40補足説明欄赤枠内(9) 　= {(∂/∂xk)[f(x1, y1, z1; ・・・; xn, yn, zn)]}i 　　　+ {(∂/∂yk)[f(x1, y1, z1; ・・・; xn, yn, zn)]}j 　　　　+ {(∂/∂zk)[f(x1, y1, z1; ・・・; xn, yn, zn)]}k　∵(5)(6)(7) 　= {(∂/∂xk)[f'(r1, ・・・, rn)]}i + {(∂/∂yk)[f'(r1, ・・・, rn)]}j + {(∂/∂zk)[f'(r1, ・・・, rn)]}k　∵(13a) ∴ (∇kf')(r1, ・・・, rn) 　　　= {(∂/∂xk)[f'(r1, ・・・, rn)]}i + {(∂/∂yk)[f'(r1, ・・・, rn)]}j + {(∂/∂zk)[f'(r1, ・・・, rn)]}k ・・・(14) ∇k[f'(r1, ・・・, rn)] という物は存在しないので、(∇kf')(r1, ・・・, rn) を ∇kf'(r1, ・・・, rn) と略記する事にします。 ∇kf'(r1, ・・・, rn) = (∇kf')(r1, ・・・, rn) ・・・(15) また、 ri = xii + yij + zik ⇒ f'(r1, r2, ・・・, rn) = f(x1, y1, z1; x2, y2, z2; ・・・; xn, yn, zn) である様な f' と f は区別しない事にします。(※2) (14)とTEC-0-1-40補足説明欄赤枠内(26)から、 (∇kf')(r1, ・・・, rn) = [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][f'(r1, ・・・, rn)] ・・・(14a) だと分かります。 ∇の添え字として番号ではなく変数を表す文字を用いる場合、関数の微分ではなく、関数の値の微分を表す物とします。 ∇x ≡ i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3) ・・・(16a) ∇y ≡ i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3) ・・・(16b) など。 ∇yf'(x, y) = ∇y[f'(x, y)] ・・・(17) です。 ∇yf'(x, y) = [∇yf'](x, y) ではありません。 文字の上にドットを付けて時間微分を表す記号法は、今までは時刻tで微分する、と考える書き方でしたが、ここ以降の補足説明欄では、以下の規則に置き換えます。 (関数を表す文字の上にドットを加筆する) ＝ (関数を表す文字の左に D を加筆する) つまり、 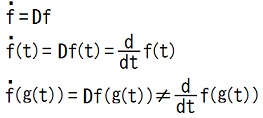という風に考え書く事にします。2016.05.11,13,14,15,17,18,20,21;2019.06.09,10 2行目の式の意味は、2つのベクトルを変数とする関数 Uik が、1つのベクトルを変数とする関数 U'ik を使って、 Uik(x, y) = U'ik(x - y) という風に表される、という意味です。 x = x1i + x2j + x3k y = y1i + y2j + y3k x - y = (x1 - y1)i + (x2 - y2)j + (x3 - y3)k だから、上の赤枠内の※1※2によって、6変数関数 Uik に対して、 Uik(x1, x2, x3; y1, y2, y3) = U'ik(x1 - y1, x2 - y2, x3 - y3) である様な3変数関数 U'ik が存在する、という意味だ、と考える事も出来ます。2016.05.10,13,17,21 2行目の条件について、COM-1-16-1〜14に補足説明が書かれています。2016.05.15 3行目の左の等号の成立 Fik = -∇iUik(ri - rk) は、 Fik(ri, rk, vi, vk, t) = -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][U'ik(ri - rk)] を略記した物です。 この式は、Fik という関数と U'ik という関数の関係を表しているだけであり、変数は何でも良いので、 Fik(x, y, u, v, w) = -[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U'ik(x - y)] すなわち Fik(x, y, u, v, w) = -∇x[U'ik(x - y)] ・・・ (1) と書いても意味は変わりません。 ∇x は、上の赤枠内(16a)で定義されています。 (1)の成立根拠は、 Fik(x, y, u, v, w) = -∇x[Uik(x, y)] ・・・ CAN-1-1-16-2の補足説明の(2) である事と、 Uik(x, y) = U'ik(x - y) ・・・ TEC-0-1-43-2の補足説明 である事です。2016.05.10,13,17,21,27 3行目の右の等号の成立 -∇iUik(ri - rk) = -∇Uik(ri - rk) は、 -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][U'ik(ri - rk)] = -(∇U'ik)(ri - rk) を略記した物です。[右辺の∇は、上の赤枠内(8)の∇です] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U'ik(x - y)] = -(∇U'ik)(x - y) すなわち -∇x[U'ik(x - y)] = -(∇U'ik)(x - y) ・・・ (2) と書いても意味は変わりません。 ∇x は、上の赤枠内(16a)で定義されています。 (2)の成立根拠は、以下です。 ∇x[U'ik(x - y)] 　= [i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U'ik(x1 - y1, x2 - y2, x3 - y3)]　∵上の赤枠内の(16a)と※1 　= {(∂/∂x1)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}i 　　　+ {(∂/∂x2)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}j 　　　　+ {(∂/∂x3)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}k　∵TEC-0-1-40補足説明欄赤枠内(26) 　= {(∂/∂z1)[U'ik(z1, z2, z3)]}i + {(∂/∂z2)[U'ik(z1, z2, z3)]}j + {(∂/∂z3)[U'ik(z1, z2, z3)]}k 　　　に z1 = x1 - y1, z2 = x2 - y2, z3 = x3 - y3 を代入して得られるベクトル 　= [i(∂/∂z1) + j(∂/∂z2) + k(∂/∂z3)][U'ik(z1, z2, z3)] に z1 = x1 - y1, z2 = x2 - y2, z3 = x3 - y3 を代入して得られるベクトル 　　　∵TEC-0-1-40補足説明欄赤枠内(26) 　= [i(∂/∂z1) + j(∂/∂z2) + k(∂/∂z3)][U'ik(z)] に z = x - y を代入して得られるベクトル　∵上の赤枠内の※1 　= (∇U'ik)(z) に z = x - y を代入して得られるベクトル　∵上の赤枠内の(9a)と※1 　= (∇U'ik)(x - y)　//2016.05.10,11,13,17,21 4行目の最も左の等号の成立 -∇Uik(ri - rk) = ∇kUik(ri - rk) は、 -(∇U'ik)(ri - rk) = [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][U'ik(ri - rk)] を略記した物です。[左辺の∇は、上の赤枠内(8)の∇です] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -(∇U'ik)(x - y) = [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][U'ik(x - y)] すなわち -(∇U'ik)(x - y) = ∇y[U'ik(x - y)] ・・・ (3) と書いても意味は変わりません。[∇y は、上の赤枠内(16b)で定義されています] (3)の成立根拠は、以下です。 ∇y[U'ik(x - y)] 　= [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][U'ik(x1 - y1, x2 - y2, x3 - y3)]　∵上の赤枠内の(16b)と※1 　= {(∂/∂y1)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}i 　　　+ {(∂/∂y2)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}j 　　　　+ {(∂/∂y3)[U'ik(x1 - y1, x2 - y2, x3 - y3)]}k　∵TEC-0-1-40補足説明欄赤枠内(26) 　= {-(∂/∂z1)[U'ik(z1, z2, z3)]}i + {-(∂/∂z2)[U'ik(z1, z2, z3)]}j + {-(∂/∂z3)[U'ik(z1, z2, z3)]}k 　　　に z1 = x1 - y1, z2 = x2 - y2, z3 = x3 - y3 を代入して得られるベクトル 　= -[i(∂/∂z1) + j(∂/∂z2) + k(∂/∂z3)][U'ik(z1, z2, z3)] に z1 = x1 - y1, z2 = x2 - y2, z3 = x3 - y3 を代入して得られるベクトル 　　　∵TEC-0-1-40補足説明欄赤枠内(26) 　= -[i(∂/∂z1) + j(∂/∂z2) + k(∂/∂z3)][U'ik(z)] に z = x - y を代入して得られるベクトル　∵上の赤枠内の※1 　= -(∇U'ik)(z) に z = x - y を代入して得られるベクトル　∵上の赤枠内の(9a)と※1 　= -(∇U'ik)(x - y)　//2016.05.10,11,13,17,21 4行目の中央の等号の成立 ∇kUik(ri - rk) = ∇kUik(ri, rk) は、 [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][U'ik(ri - rk)] = [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][Uik(ri, rk)] を略記した物です。 この式は、ri, rk が何であっても成り立つ事を主張する物なので、 [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][U'ik(x - y)] = [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][Uik(x, y)] すなわち ∇y[U'ik(x - y)] = ∇y[Uik(x, y)] ・・・ (4) と書いても意味は変わりません。[∇y は、上の赤枠内(16b)で定義されています] (4)の成立根拠は、 U'ik(x - y) = Uik(x, y) ・・・ 2行目の式の補足説明 である事です。2016.05.10,11,13,17,21 4行目の最も右の等号の成立 ∇kUik(ri, rk) = ∇kUki(rk, ri) は、 [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][Uik(ri, rk)] = [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][Uki(rk, ri)] を略記した物です。 この式は、ri, rk が何であっても成り立つ事を主張する物なので、 [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][Uik(x, y)] = [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][Uki(y, x)] すなわち ∇y[Uik(x, y)] = ∇y[Uki(y, x)] ・・・ (5) と書いても意味は変わりません。[∇y は、上の赤枠内(16b)で定義されています] (5)の成立根拠は、 Uik(x, y) = Uki(y, x) ・・・ CAN-1-1-16-3の式の補足説明 である事です。2016.05.10,11,13,17,21 5行目の等号の成立 ∇kUki(rk, ri) = -Fki は、 [i(∂/∂xk) + j(∂/∂yk) + k(∂/∂zk)][Uki(rk, ri)] = -Fki(rk, ri, vk, vi, t) を略記した物です。 この式は、ri, rk, vi, vk, t が何であっても成り立つ事を主張する物なので、 [i(∂/∂y1) + j(∂/∂y2) + k(∂/∂y3)][Uki(y, x)] = -Fki(y, x, v, u, w) すなわち ∇y[Uki(y, x)] = -Fki(y, x, v, u, w) ・・・ (6) と書いても意味は変わりません。[∇y は、上の赤枠内(16b)で定義されています] (6)の成立根拠は、 Fki(y, x, v, u, w) = -∇y[Uki(y, x)] ・・・ CAN-1-1-16-2の補足説明の(2) である事です。2016.05.10,11,13,17,18,21,27 3〜5行目の計算をまとめると、 Fik(x, y, u, v, w) 　= -∇x[U'ik(x - y)] ・・・ (1) 　= -(∇U'ik)(x - y) ・・・ (2) 　= ∇y[U'ik(x - y)] ・・・ (3) 　= ∇y[Uik(x, y)] ・・・ (4) 　= ∇y[Uki(y, x)] ・・・ (5) 　= -Fki(y, x, v, u, w) ・・・ (6) だから、これでCAN-1-1-15-16の式の成立が証明された事に成ります。2016.05.10,13,14,17,21 6行目について。 Fik(x, y, u, v, w) = -Fki(y, x, v, u, w) ならば内力が作用反作用の法則に従う事、はCAN-1-1-15-16〜18に対する補足説明に書かれています。2016.05.11,17 9行目の式の意味は、2つのベクトルを変数とする関数 Uik が、1つの実数を変数とする関数 U''ik を使って、 Uik(x, y) = U''ik(|x - y|) という風に表される、という意味です。 x = x1i + x2j + x3k y = y1i + y2j + y3k x - y = (x1 - y1)i + (x2 - y2)j + (x3 - y3)k |x - y| = √[(x1 - y1)2 + (x2 - y2)2 + (x3 - y3)2] だから、上の赤枠内の※2によって、6変数関数 Uik に対して、 Uik(x1, x2, x3; y1, y2, y3) = U''ik(√[(x1 - y1)2 + (x2 - y2)2 + (x3 - y3)2]) である様な1変数関数 U''ik が存在する、という意味だ、と考える事も出来ます。2016.05.14,17,21 10行目の「上記」とは、2〜6行目の内容の事です。2016.05.14 10行目の内容の根拠は、 Uik(x, y) = U''ik(|x - y|) ならば U'ik(z) = U''ik(|z|) によって定義される U'ik は Uik(x, y) = U'ik(x - y) という条件を満たす事です。 U'ik(x - y) = U''ik(|x - y|) = Uik(x, y) したがって、9行目の条件は2行目の条件の十分条件です。2016.05.14,17 11〜18行目の最左辺以外では、負号(-)が書き忘れられています。 本当は負号(-)が必要です。2016.05.14 11,12行目の左の等号の成立 Fik = -∇iUik(|ri - rk|) は、 Fik(ri, rk, vi, vk, t) = -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][U''ik(|ri - rk|)] を略記した物です。 この式は、Fik という関数と U''ik という関数の関係を表しているだけであり、変数は何でも良いので、 Fik(x, y, u, v, w) = -[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U''ik(|x - y|)] すなわち Fik(x, y, u, v, w) = -∇x[U''ik(|x - y|)] ・・・ (7) と書いても意味は変わりません。[∇x は、上の赤枠内(16a)で定義されています] (7)の成立根拠は、 Fik(x, y, u, v, w) = -∇x[Uik(x, y)] ・・・ CAN-1-1-16-2の補足説明の(2) である事と、 Uik(x, y) = U''ik(|x - y|) ・・・TEC-0-1-43-9への補足説明 である事です。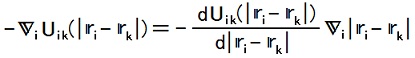2016.05.14,17,21,27 11,12行目の右の等号の成立 は、 -[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)][U''ik(|ri - rk|)] 　= -[(DU''ik)(|ri - rk|)]{[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)]|ri - rk|} を崩して書いた物です。[D は上の赤枠内(2)で定義されています] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U''ik(|x - y|)] 　= -[(DU''ik)(|x - y|)]{[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]|x - y|} すなわち -∇x[U''ik(|x - y|)] = -[(DU''ik)(|x - y|)](∇x|x - y|) ・・・ (8) と書いても意味は変わりません。[∇x は、上の赤枠内(16a)で定義されています] (8)の成立根拠は、以下です。 (∂/∂xk)[U''ik(|x - y|)] 　= (∂z/∂xk)(d/dz)[U''ik(z)]　(z = |x - y|) 　= (∂|x - y|/∂xk)[(DU''ik)(|x - y|)]　∵上の赤枠内(2) 　= [(DU''ik)(|x - y|)][(∂/∂xk)|x - y|] ∴ ∇x[U''ik(|x - y|)] 　　= [i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)][U''ik(|x - y|)] 　　= {(∂/∂x1)[U''ik(|x - y|)]}i 　　　　+ {(∂/∂x2)[U''ik(|x - y|)]}j 　　　　　+ {(∂/∂x3)[U''ik(|x - y|)]}k　∵TEC-0-1-40補足説明欄赤枠内(26) 　　= {[(DU''ik)(|x - y|)][(∂/∂x1)|x - y|]}i 　　　　+ {[(DU''ik)(|x - y|)][(∂/∂x2)|x - y|]}j 　　　　　+ {[(DU''ik)(|x - y|)][(∂/∂x3)|x - y|]}k 　　= [(DU''ik)(|x - y|)]{[(∂/∂x1)|x - y|]i + [(∂/∂x2)|x - y|]j + [(∂/∂x3)|x - y|]k} 　　= [(DU''ik)(|x - y|)]{[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]|x - y|}　∵TEC-0-1-40補足説明欄赤枠内(26) 　　= [(DU''ik)(|x - y|)](∇x|x - y|)　//2016.05.14,17,18,21;2019.05.28 13,14行目の等号の成立 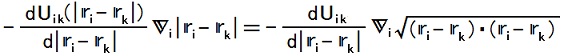は、 -[(DU''ik)(|ri - rk|)]{[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)]|ri - rk|} 　= -[(DU''ik)(|ri - rk|)]{[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)]√[(ri - rk)・(ri - rk)]} を崩して書いた物です。[D は上の赤枠内(2)で定義されています] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -[(DU''ik)(|x - y|)]{[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]|x - y|} 　= -[(DU''ik)(|x - y|)]{[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]√[(x - y)・(x - y)]} すなわち -[(DU''ik)(|x - y|)](∇x|x - y|) = -[(DU''ik)(|x - y|)]{∇x√[(x - y)・(x - y)]} ・・・ (9) と書いても意味は変わりません。[∇x は上の赤枠内(16a)で定義されています] (9)の成立根拠は、 |x - y| = √[(x - y)・(x - y)] である事です。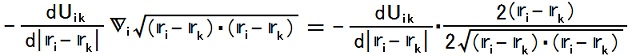2016.05.14,17,21;2019.05.28 15,16行目の等号の成立 は、 -[(DU''ik)(|ri - rk|)]{[i(∂/∂xi) + j(∂/∂yi) + k(∂/∂zi)]√[(ri - rk)・(ri - rk)]} 　= -[(DU''ik)(|ri - rk|)]・2(ri - rk)/{2√[(ri - rk)・(ri - rk)]} を崩して書いた物です。[D は上の赤枠内(2)で定義されています] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -[(DU''ik)(|x - y|)]{[i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]√[(x - y)・(x - y)]} 　= -[(DU''ik)(|x - y|)]・2(x - y)/{2√[(x - y)・(x - y)]} すなわち -[(DU''ik)(|x - y|)]{∇x√[(x - y)・(x - y)]} 　= -[(DU''ik)(|x - y|)]・2(x - y)/{2√[(x - y)・(x - y)]} ・・・ (10) と書いても意味は変わりません。[∇x は、上の赤枠内(16a)で定義されています] (10)の成立根拠は、以下です。 (∂/∂xk)√[(x - y)・(x - y)] 　= (∂/∂xk)√[(x1 - y1)2 + (x2 - y2)2 + (x3 - y3)2] 　= (∂z/∂xk)[(d/dz)√z]　[z = (x1 - y1)2 + (x2 - y2)2 + (x3 - y3)2] 　= 2(xk - yk)[1/(2√z)] 　= 2(xk - yk)/{2√[(x - y)・(x - y)]}　∵ z = (x - y)・(x - y) ∴ ∇x√[(x - y)・(x - y)] 　　= [i(∂/∂x1) + j(∂/∂x2) + k(∂/∂x3)]√[(x - y)・(x - y)] 　　= {(∂/∂x1)√[(x - y)・(x - y)]}i 　　　　+ {(∂/∂x2)√[(x - y)・(x - y)]}j 　　　　　+ {(∂/∂x3)√[(x - y)・(x - y)]}k　∵TEC-0-1-40補足説明欄赤枠内(26) 　　= (2(x1 - y1)/{2√[(x - y)・(x - y)]})i 　　　　+ (2(x2 - y2)/{2√[(x - y)・(x - y)]})j 　　　　　+ (2(x3 - y3)/{2√[(x - y)・(x - y)]})k 　　= (2/{2√[(x - y)・(x - y)]})[(x1 - y1)i + (x2 - y2)j + (x3 - y3)k] 　　= (2/{2√[(x - y)・(x - y)]})(x - y) 　　= 2(x - y)/{2√[(x - y)・(x - y)]}　//2016.05.14,17,18,21;2019.05.28 17,18行目の等号の成立 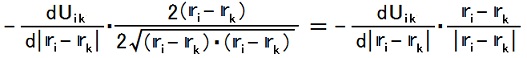は、 -[(DU''ik)(|ri - rk|)]・2(ri - rk)/{2√[(ri - rk)・(ri - rk)]} = -[(DU''ik)(|ri - rk|)](ri - rk)/|ri - rk| を崩して書いた物です。[D は上の赤枠内(2)で定義されています] この式は、ri, rk が何であっても成り立つ事を主張する物なので、 -[(DU''ik)(|x - y|)]・2(x - y)/{2√[(x - y)・(x - y)]} = -[(DU''ik)(|x - y|)](x - y)/|x - y| ・・・ (11) と書いても意味は変わりません。 (11)の成立根拠は、以下です。 2(x - y)/{2√[(x - y)・(x - y)]} 　= (x - y)/{√[(x - y)・(x - y)]} 　= (x - y)/[√(|x - y|2)] 　= (x - y)/|x - y|　//2016.05.14,17,18,21;2019.05.28 11〜18行目の計算をまとめると、 Fik(x, y, u, v, w) 　= -∇x[U''ik(|x - y|)] ・・・ (7) 　= -[(DU''ik)(|x - y|)](∇x|x - y|) ・・・ (8) 　= -[(DU''ik)(|x - y|)]{∇x√[(x - y)・(x - y)]} ・・・ (9) 　= -[(DU''ik)(|x - y|)]・2(x - y)/{2√[(x - y)・(x - y)]} ・・・ (10) 　= -[(DU''ik)(|x - y|)](x - y)/|x - y| ・・・ (11) であり、この事から (x - y)×Fik(x, y, u, v, w) = 0 が言えるので、これでCAN-1-1-15-25の式の成立が証明された事に成ります。2016.05.14,17,21 19行目について。 (x - y)×Fik(x, y, u, v, w) = 0 ならば内力が中心力に成る事、はCAN-1-1-15-24〜26に対する補足説明に書かれています。2016.05.14,17
▲このページの上端へ行く
【SEOテキスト】03.12.29宇田雄一CAN-1-1-15-16〜18,16-2〜5,Uik(ri,rk)=Uik(ri-rk)の場合、Fik=-∇i Uik(ri-rk)=-∇Uik(ri-rk)=∇k Uik(ri-rk)=∇k Uik(ri,rk)=∇k Uki(rk,ri)=-Fki故に作用反作用の法則が内力に関して成り立つ。CAN-1-1-15-24〜26,16-2〜5,Uik(ri,rk)=Uik(|ri-rk|)の場合、まず上記より内力に関して作用反作用の法則が成り立つ。さらにFik=∇i Uik(|ri-rk|)=dUik(|ri-rk|)/d|ri-rk|∇i|ri-rk|=dUik/d|ri-rk|∇i√ (ri-rk)・(ri-rk)=dUik/d|ri-rk|・2(ri-rk)/2√ (ri-rk)・(ri-rk)=dUik/d|ri-rk|・ ri-rk/|ri-rk|故に内力は中心力である。