
ژں‚جƒyپ[ƒW
‘O‚جƒyپ[ƒW
–عژں
CAN-1-1-15
CAN-1-1-16
پy•â‘«گà–¾—“پz
2,3چs–ع‚إ‚حپAri(t) ‚ً ri ‚ئ—ھ‹L‚µپA
4پ`9چs–ع‚إ‚حپACAN-1-1-15-7‚ج Fi(t) ‚ً Fi ‚ئ—ھ‹L‚µپACAN-1-1-15-8‚ج Fik(t) ‚ً Fik ‚ئ—ھ‹L‚µ‚ؤ‚¢‚ـ‚·پB2016.05.09,15
4,5چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚حپACAN-1-1-15-5,6‚جژ®‚إ‚·پB2016.02.11
6,7چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚حپAˆب‰؛‚إ‚·پB
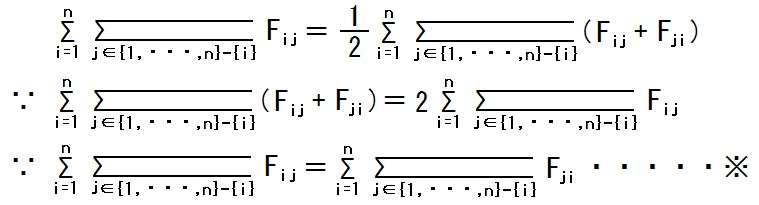
پ¦‚جگ¬—§‚حپAچ¶•س‚à‰E•س‚àپuFij ‚ً‘و i چs‘و j —ٌ‚ةژ‚آچs—ٌ‚ج‘خٹpگ¬•ھˆبٹO‚ج‘S‚ؤ‚جگ¬•ھ‚ً‘«‚¹پv‚ئ‚¢‚¤ژ®‚ةگ¬‚ء‚ؤ‚¢‚éژ–پA‚©‚ç•ھ‚©‚è‚ـ‚·پB2016.02.11,13;2016.03.07;2019.06.03
9,15چs–ع‚ج 0 ‚حŒë‚è‚إ‚·پB
گ³‚µ‚‚ح 0 ‚إ‚·پB
‚آ‚ـ‚èپAگ”ژڑ‚جƒ[ƒچ‚إ‚ح‚ب‚ƒ[ƒچƒxƒNƒgƒ‹‚ًڈ‘‚•K—v‚ھ‚ ‚è‚ـ‚µ‚½پB2016.02.13;2016.03.07
8چs–ع‚جڈc“™چ†‚جگ¬—§چھ‹’‚حپAFji(t) = -Fij(t) ‚إ‚ ‚éژ–‚إ‚·پB
Fji(t) = -Fij(t) ‚جگ¬—§چھ‹’‚حپACAN-1-1-15-16پ`18‚ض‚ج•â‘«گà–¾‚ةڈ‘‚©‚ê‚ؤ‚¢‚ـ‚·پB2016.02.11;2016.05.09,15
12پ`24چs–ع‚إ‚حپAri(t) ‚ً ri ‚ئ—ھ‹L‚µپA
14,15چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚حپAگد‚ج”÷•ھ–@‚إ‚·پB2016.05.15
14,15چs–ع‚ج”gگü•”•ھ‚ھƒ[ƒچƒxƒNƒgƒ‹‚ةگ¬‚éژ–‚حپA•½چs‚بƒxƒNƒgƒ‹“¯ژm‚جٹOگد‚حƒ[ƒچƒxƒNƒgƒ‹‚إ‚ ‚éژ–پA‚¨‚و‚ر dri(t)/dt ‚ئ midri(t)/dt ‚ھ•½چs‚إ‚ ‚éژ–پA‚©‚ç•ھ‚©‚è‚ـ‚·پB2016.02.13;2016.03.07;2016.05.15
16پ`24چs–ع‚إ‚حپACAN-1-1-15-7‚ج Fi(t) ‚ً Fi ‚ئ—ھ‹L‚µپACAN-1-1-15-8‚ج Fik(t) ‚ً Fik ‚ئ—ھ‹L‚µ‚ؤ‚¢‚ـ‚·پB2016.05.09,15
16,17چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚حپACAN-1-1-15-5,6‚جژ®‚إ‚·پB2016.02.13
20چs–ع‚جڈc“™چ†‚جگ¬—§چھ‹’‚حپA6,7چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚ئ“¯—l‚إ‚·پB
‚½‚¾‚µپA6,7چs–ع‚ج“™چ†‚ئˆل‚ء‚ؤپA20چs–ع‚جڈc“™چ†‚إ‚حپAriپ~Fij ‚ئ‚¢‚¤ƒxƒNƒgƒ‹‚ً‘و i چs‘و j —ٌ‚ةژ‚آچs—ٌپA‚ًچl‚¦‚ـ‚·پB2016.02.13,18;2016.03.07;2016.05.15;2019.06.03
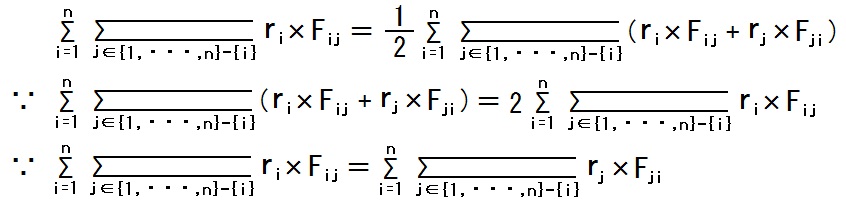
23چs–ع‚جڈc“™چ†‚جگ¬—§چھ‹’‚حپAFji(t) = -Fij(t) ‚إ‚ ‚éژ–‚إ‚·پB
Fji(t) = -Fij(t) ‚جگ¬—§چھ‹’‚حپACAN-1-1-15-16پ`18‚ض‚ج•â‘«گà–¾‚ةڈ‘‚©‚ê‚ؤ‚¢‚ـ‚·پB2016.02.13;2016.05.09,13,15
24چs–ع‚ج“™چ†‚جگ¬—§
[ri(t) - rj(t)]پ~Fij(t) = 0
‚جچھ‹’‚حپACAN-1-1-15-24پ`26‚ض‚ج•â‘«گà–¾‚ةڈ‘‚©‚ê‚ؤ‚¢‚ـ‚·پB2016.02.13;2016.05.09,13,15
27پ`30چs–ع‚إ‚حپA
27پ`30چs–ع‚إ‚حپAU(r1(t), پEپEپE, rn(t)) ‚ً U ‚ئ—ھ‹L‚µ‚ؤ‚¢‚ـ‚·پB
U ‚حCAN-1-1-16-14,15‚إ’è‹`‚³‚ê‚ؤ‚¢‚éٹضگ”‚إ‚·پB2016.05.18,24;2019.06.12
29,30چs–ع‚ج (dri/dt)پEپقiU ‚حپA
(dri/dt)پE{[i(پف/پفxi) + j(پف/پفyi) + k(پف/پفzi)][U(r1, پEپEپE, rn)]}
‚ً—ھ‹L‚µ‚½•¨‚إ‚·پB
‚½‚¾‚µ ri = xii + yij + zik ‚ئ‚µ‚ـ‚·پB2016.05.08,09,14,16,18,20,24;2019.06.12
29,30چs–ع‚ج“™چ†‚جگ¬—§چھ‹’‚حپA
(d/dt)|dri/dt|2
پ@= (d/dt)[(dri/dt)پE(dri/dt)]
پ@= [(d/dt)(dri/dt)]پE(dri/dt) + (dri/dt)پE[(d/dt)(dri/dt)]پ@پوگد‚ج”÷•ھ–@
پ@= 2[(d/dt)(dri/dt)]پE(dri/dt)
پ@= 2(d2ri/dt2)پE(dri/dt)
‚إ‚ ‚éژ–‚ئپA
(d/dt)[U(r1, پEپEپE, rn)]
پ@= ƒ°i=1n { (dxi/dt)[پفU(r1, پEپEپE, rn)/پفxi] + (dyi/dt)[پفU(r1, پEپEپE, rn)/پفyi] + (dzi/dt)[پفU(r1, پEپEپE, rn)/پفzi] }
پ@= ƒ°i=1n [(dxi/dt)i + (dyi/dt)j + (dzi/dt)k]پE{[پفU(r1, پEپEپE, rn)/پفxi]i + [پفU(r1, پEپEپE, rn)/پفyi]j + [پفU(r1, پEپEپE, rn)/پفzi]k}
پ@= ƒ°i=1n (dri/dt)پE{[i(پف/پفxi) + j(پف/پفyi) + k(پف/پفzi)][U(r1, پEپEپE, rn)]}پ@پو‰؛‚جگشکg“à‚ج(26)
‚إ‚ ‚éژ–‚إ‚·پB(ri = xii + yij + zik)پ@//2016.05.08,15,16,18,20,24;2019.06.12
| ˆب‰؛‚ة‚¨‚¢‚ؤ‚حپAپuٹضگ”پv‚ئپuٹضگ”‚ج’lپv‚ً‹و•ت‚µ‚ـ‚·پB(CAN-1-1-15-7,8‚ج•â‘«گà–¾) f, g ‚ًٹضگ”(’l‚ھژہگ”‚â•،‘fگ”‚إ‚ ‚é—l‚بٹضگ”)‚ئ‚·‚é‚ئ‚«پAf + g ‚حپA (f + g)(x) = f(x) + g(x) پEپEپE(1) ‚آ‚ـ‚èپAx ‚إ‚ج’l‚ھ f(x) + g(x) ‚إ‚ ‚éژ–پA‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éٹضگ”‚إ‚·پB ‚³‚ç‚ةپAc ‚ًژہگ”‚â•،‘fگ”‚ئ‚·‚é‚ئ‚«پAcf ‚حپA (cf)(x) = c[f(x)] پEپEپE(2) ‚آ‚ـ‚èپAx ‚إ‚ج’l‚ھ c[f(x)] ‚إ‚ ‚éژ–پA‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éٹضگ”‚إ‚·پB (cf)(x) ‚ئ c[f(x)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ cf(x) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB cf(x) پك (cf)(x) = c[f(x)] پEپEپE(2a) a, b ‚ًژہگ”‚â•،‘fگ”‚ئ‚·‚é‚ئ‚«پAaf + bg ‚ح x ‚إ‚ج’l‚ھ (af + bg)(x) = a[f(x)] + b[g(x)] پEپEپE(3) ‚إ‚ ‚éژ–‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éٹضگ”‚¾پA‚ئ‚¢‚¤ژ–‚ھˆبڈم‚ج’è‹`‚©‚ç•ھ‚©‚è‚ـ‚·پB (af + bg)(x) پ@= (af)(x) + (bg)(x)پ@پو(1) پ@= a[f(x)] + b[g(x)]پ@پو(2) f, g ‚ھƒxƒNƒgƒ‹’lٹضگ”(’l‚ھƒxƒNƒgƒ‹‚إ‚ ‚é—l‚بٹضگ”)‚جڈêچ‡‚ة‚àپAf + g, cf ‚حپA‚»‚ꂼ‚êپA (f + g)(x) = f(x) + g(x) پEپEپE(4) (cf)(x) = c[f(x)] پEپEپE(5) ‚ئ‚¢‚¤ڈًŒڈ‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éƒxƒNƒgƒ‹’lٹضگ”‚إ‚ ‚èپA‚±‚جژ–‚©‚çپA af + bg ‚ح (af + bg)(x) = a[f(x)] + b[g(x)] پEپEپE(6) ‚ئ‚¢‚¤ڈًŒڈ‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éƒxƒNƒgƒ‹’lٹضگ”‚¾پA‚ئ‚¢‚¤ژ–‚ھ•ھ‚©‚è‚ـ‚·پB f(x) ‚ئ g(x) ‚ھƒxƒNƒgƒ‹‚إ‚ ‚éژ–پA‚ة‹C‚ً•t‚¯‚ؤ‰؛‚³‚¢پB (cf)(x) ‚ئ c[f(x)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ cf(x) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB cf(x) پك (cf)(x) = c[f(x)] پEپEپE(5a) f ‚ًٹضگ”‚ئ‚µپAv ‚ًƒxƒNƒgƒ‹‚ئ‚·‚é‚ئ‚«پAvf ‚حپA (vf)(x) = [f(x)]v پEپEپE(7) ‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éƒxƒNƒgƒ‹’lٹضگ”‚إ‚·پB (vf)(x) ‚ئ v[f(x)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ vf(x) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB vf(x) پك (vf)(x) = v[f(x)] پEپEپE(7a) f, g ‚ًٹضگ”‚ئ‚µپAu, v ‚ًƒxƒNƒgƒ‹‚ئ‚·‚é‚ئ‚«پAuf + vg ‚ح x ‚إ‚ج’l‚ھ (uf + vg)(x) = [f(x)]u + [g(x)]v پEپEپE(8) ‚إ‚ ‚éژ–‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éƒxƒNƒgƒ‹’lٹضگ”‚¾پA‚ئ‚¢‚¤ژ–‚ھˆبڈم‚ج’è‹`‚©‚ç•ھ‚©‚è‚ـ‚·پB (uf + vg)(x) پ@= (uf)(x) + (vg)(x)پ@پو(4) پ@= [f(x)]u + [g(x)]vپ@پو(7) f, g, h ‚ًٹضگ”‚ئ‚µپAi, j, k ‚ً CAN-1-1-1-11پ`16 ‚ج’PˆتƒxƒNƒgƒ‹‚ئ‚·‚é‚ئ‚«پAx ‚إ‚ج’l‚ھ (if + jg + kh)(x) = [f(x)]i + [g(x)]j + [h(x)]k پEپEپE(9) ‚إ‚ ‚éژ–‚ة‚و‚ء‚ؤ’è‹`‚³‚ê‚éƒxƒNƒgƒ‹’lٹضگ”‚ھ if + jg + kh ‚ئڈ‘‚©‚ê‚éژ–‚àپA(8)‚ئ“¯—l‚إ‚·پB f, g, h ‚ًٹضگ”‚ئ‚µپAa, b, c ‚ًژہگ”‚â•،‘fگ”‚ئ‚·‚é‚ئ‚«پAaf + bg + ch ‚ئ‚¢‚¤ٹضگ”‚ًپA (ai + bj + ck)پE(if + jg + kh) ‚ئ‚àڈ‘‚ژ–‚ة‚µ‚ـ‚·پB (ai + bj + ck)پE(if + jg + kh) پك af + bg + ch پEپEپE(10) ‚±‚ê‚حپAƒxƒNƒgƒ‹“¯ژm‚ج“àگد‚ة•ي‚ء‚ؤ‚جژ–‚إ‚·پB ‚±‚±‚ـ‚إ‚ج’è‹`‚حپAپuf, g, h ‚ً‰‰ژZژq(ٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚·‚éپvپuf, g ‚ً‰‰ژZژq(ٹضگ”‚ًƒxƒNƒgƒ‹’lٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚·‚éپvپux ‚ًٹضگ”‚ئ‚·‚éپv‚ئ‚¢‚¤•—‚ة“ا‚ف‘ض‚¦‚ؤ‚àپA’ت—p‚µ‚ـ‚·پB ‚»‚جژ–‚ًپAˆب‰؛‚ةڈ‘‚«‚ـ‚·پB F, G ‚ً‰‰ژZژq(ٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚µپAa, b, c ‚ًژہگ”‚â•،‘fگ”‚ئ‚µپAf ‚ًٹضگ”‚ئ‚·‚é‚ئ‚«پA (F + G)(f) پك F(f) + G(f) پEپEپE(11) (cF)(f) پك c[F(f)] پEپEپE(12) (aF + bG)(f) = a[F(f)] + b[G(f)] پEپEپE(13) ‚±‚ê‚ç‚جژ®‚ج‰E•س‚ج F(f) ‚ئ G(f) ‚ح‚¢‚¸‚ê‚àٹضگ”‚إ‚ ‚éژ–پA‚ة‹C‚ً•t‚¯‚ؤ‰؛‚³‚¢پB (cF)(f) ‚ئ c[F(f)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ cF(f) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB cF(f) پك (cF)(f) = c[F(f)] پEپEپE(12a) F, G ‚ً‰‰ژZژq(ٹضگ”‚ًƒxƒNƒgƒ‹’lٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚µپAa, b, c ‚ًژہگ”‚â•،‘fگ”‚ئ‚µپAf ‚ًٹضگ”‚ئ‚·‚é‚ئ‚«پA (F + G)(f) پك F(f) + G(f) پEپEپE(14) (cF)(f) پك c[F(f)] پEپEپE(15) (aF + bG)(f) = a[F(f)] + b[G(f)] پEپEپE(16) ‚±‚ê‚ç‚جژ®‚ج‰E•س‚ج F(f) ‚ئ G(f) ‚ح‚¢‚¸‚ê‚àƒxƒNƒgƒ‹’lٹضگ”‚إ‚ ‚éژ–پA‚ة‹C‚ً•t‚¯‚ؤ‰؛‚³‚¢پB (cF)(f) ‚ئ c[F(f)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ cF(f) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB cF(f) پك (cF)(f) = c[F(f)] پEپEپE(15a) F, G ‚ً‰‰ژZژq(ٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚µپAu, v ‚ًƒxƒNƒgƒ‹‚ئ‚µپAf ‚ًٹضگ”‚ئ‚·‚é‚ئ‚«پA (uF)(f) پك u[F(f)] پEپEپE(17) (uF + vG)(f) = u[F(f)] + v[G(f)] پEپEپE(18) ‚±‚ê‚ç‚جژ®‚ج‰E•س‚ج F(f) ‚ئ G(f) ‚ح‚¢‚¸‚ê‚àٹضگ”‚إ‚ ‚éژ–پA‚ة‹C‚ً•t‚¯‚ؤ‰؛‚³‚¢پB (uF)(f) ‚ئ u[F(f)] ‚ھˆل‚ي‚ب‚¢‚ج‚إپAٹ‡Œت‚ًڈب—ھ‚µ‚ؤ uF(f) ‚ئ‚¢‚¤ڈ‘‚«•û‚à—p‚¢‚ç‚ê‚ـ‚·پB uF(f) پك (uF)(f) = u[F(f)] پEپEپE(17a) F, G, H ‚ً‰‰ژZژq(ٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚µپAf ‚ًٹضگ”‚ئ‚·‚é‚ئ‚«پA (iF + jG + kH)(f) پك i[F(f)] + j[G(f)] + k[H(f)] پEپEپE(19) ‚±‚ê‚ç‚جژ®‚ج‰E•س‚ج F(f) ‚ئ G(f) ‚ئ H(f) ‚ح‚¢‚¸‚ê‚àٹضگ”‚إ‚ ‚éژ–پA‚ة‹C‚ً•t‚¯‚ؤ‰؛‚³‚¢پB F, G, H ‚ً‰‰ژZژq(ٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ)‚ئ‚µپAa, b, c ‚ًژہگ”‚â•،‘fگ”‚ئ‚·‚é‚ئ‚«پAaF + bG + cH ‚ئ‚¢‚¤‰‰ژZژq‚ًپA (ai + bj + ck)پE(iF + jG + kH) ‚ئ‚àڈ‘‚ژ–‚ة‚µ‚ـ‚·پB (ai + bj + ck)پE(iF + jG + kH) پك aF + bG + cH پEپEپE(20) ٹضگ”‚ج’l‚ً”÷•ھ‚·‚鉉ژZژq(TEC-0-1-43‚ج•â‘«گà–¾—“‚جگشکg“à)‚ة‚آ‚¢‚ؤ‚àپAˆبڈم‚ئ“¯—l‚ج‹Lچ†–@‚ً’è‹`‚µ‚ؤ‚¨‚«‚ـ‚·پB [c(d/dx)][f(x)] پك c{(d/dx)[f(x)]} پEپEپE(21)پ@پ¨پ@c(d/dx)[f(x)] ‚ئڈ‘‚¢‚ؤ‚à‚و‚¢ [(پف/پفx) + (پف/پفy)][f(x, y, پEپEپE)] پك (پف/پفx)[f(x, y, پEپEپE)] + (پف/پفy)[f(x, y, پEپEپE)] پEپEپE(22) [a(پف/پفx) + b(پف/پفy)][f(x, y, پEپEپE)] = a{(پف/پفx)[f(x, y, پEپEپE)]} + b{(پف/پفy)[f(x, y, پEپEپE)]} پEپEپE(23) [v(d/dx)][f(x)] پك {(d/dx)[f(x)]}v پEپEپE(24) [u(پف/پفx) + v(پف/پفy)]f(x, y, پEپEپE) = {(پف/پفx)[f(x, y, پEپEپE)]}u + {(پف/پفy)[f(x, y, پEپEپE)]}v پEپEپE(25) [i(پف/پفx) + j(پف/پفy) + k(پف/پفz)][f(x, y, z)] = {(پف/پفx)[f(x, y, z)]}i + {(پف/پفy)[f(x, y, z)]}j + {(پف/پفz)[f(x, y, z)]}k پEپEپE(26) (ai + bj + ck)پE[i(پف/پفx) + j(پف/پفy) + k(پف/پفz)] پك a(پف/پفx) + b(پف/پفy) + c(پف/پفz) پEپEپE(27) (vپEپقx)[f(x, پEپEپE)] پ@= {(v1i + v2j + v3k)پE[i(پف/پفx1) + j(پف/پفx2) + k(پف/پفx3)]}[f(x, پEپEپE)] پ@= [v1(پف/پفx1) + v2(پف/پفx2) + v3(پف/پفx3)][f(x, پEپEپE)]پ@پو(27) پ@= v1{(پف/پفx1)[f(x, پEپEپE)]} + v2{(پف/پفx2)[f(x, پEپEپE)]} + v3{(پف/پفx3)[f(x, پEپEپE)]}پ@پو(23) پ@= (v1i + v2j + v3k)پE({(پف/پفx1)[f(x, پEپEپE)]}i + {(پف/پفx2)[f(x, پEپEپE)]}j + {(پف/پفx3)[f(x, پEپEپE)]}k) پ@= (v1i + v2j + v3k)پE{[i(پف/پفx1) + j(پف/پفx2) + k(پف/پفx3)][f(x, پEپEپE)]}پ@پو(26) پ@= vپE{پقx[f(x, پEپEپE)]} پEپEپE(28)پ@پ¨پ@vپEپقx[f(x, پEپEپE)] ‚ئڈ‘‚¢‚ؤ‚à‚و‚¢ ‚½‚¾‚µپAپقx ‚ح TEC-0-1-43•â‘«گà–¾—“گشکg“à(16a)‚إ’è‹`‚³‚ê‚ؤ‚¢‚ـ‚·پB ˆب‰؛‚إ‚حپATEC-0-1-43‚ج•â‘«گà–¾—“‚جگشکg“à‚جڈ”’è‹`‚ًچج—p‚µ‚ـ‚·پB TEC-0-1-43•â‘«گà–¾—“گشکg“à(5)(6)(7)‚إ’è‹`‚³‚ê‚ؤ‚¢‚éپف1, پف2, پف3 ‚حپA‚¢‚¸‚ê‚àٹضگ”‚ًٹضگ”‚ةژت‚·ژت‘œ(‰‰ژZژq)‚¾‚©‚çپA”Cˆس‚جƒxƒNƒgƒ‹ v = ai + bj + ck ‚ئپA”Cˆس‚جٹضگ” f ‚ة‘خ‚µ‚ؤپA (vپEپق)(f) = [(ai + bj + ck)پE(iپف1 + jپف2 + kپف3)](f)پ@پوTEC-0-1-43•â‘«گà–¾—“گشکg“à(8) پ@= (aپف1 + bپف2 + cپف3)(f)پ@پو(20) پ@= a[پف1(f)] + b[پف2(f)] + c[پف3(f)]پ@پو(13) پ@= (ai + bj + ck)پE{i[پف1(f)] + j[پف2(f)] + k[پف3(f)]}پ@پو(10) پ@= (ai + bj + ck)پE[(iپف1 + jپف2 + kپف3)(f)]پ@پو(19) پ@= vپE[پق(f)]پ@پوTEC-0-1-43•â‘«گà–¾—“گشکg“à(8) ‚±‚جŒ‹‰ت‚ًپAڈo—ˆ‚邾‚¯ٹ‡Œت‚ًڈب—ھ‚µ‚ؤڈ‘‚‚ئپA (vپEپق)f = vپE(پقf) پEپEپE(29) ‚µ‚½‚ھ‚ء‚ؤپA‚±‚جژ®‚جٹ‡Œت‚àڈب—ھ‚إ‚«‚ـ‚·پB vپEپقf پك (vپEپق)f = vپE(پقf) پEپEپE(30) ‚³‚ؤپAf(x) ‚ح vپEپق‚ج•دˆو‚جŒ³‚إ‚àپق‚ج•دˆو‚جŒ³‚إ‚à‚ب‚¢‚ج‚إپAvپEپقf(x) ‚ً vپEپق[f(x)] ‚ئ‰ًژك‚·‚éژ–‚ح•s‰آ”\‚إ‚·پB ‚µ‚½‚ھ‚ء‚ؤ vپEپقf(x) ‚حپAvپE[(پقf)(x)] ‚ئ‰ًژك‚³‚ê‚é‚©پA‚ـ‚½‚ح [(vپEپق)f](x) ‚ئ‰ًژك‚³‚ê‚é‚©پA[vپE(پقf)](x) ‚ئ‰ًژك‚³‚ê‚邵‚©‚ ‚è‚ـ‚¹‚ٌپB ‚µ‚©‚µپA3‚آ‚ج‰ًژك‚حچ·‚ًگ¶‚ـ‚ب‚¢‚ج‚إپAvپEپقf(x) ‚ئ‚¢‚¤ڈ‘‚«•û‚ً‚µ‚ؤ‚àپAˆس–،‚جB–†‚³‚حگ¶‚¶‚ـ‚¹‚ٌپB vپEپقf(x) پك vپE[(پقf)(x)] = [(vپEپق)f](x) = [vپE(پقf)](x) پEپEپE(31) 3‚آ‚ج‰ًژك‚ھچ·‚ًگ¶‚ـ‚ب‚¢ژ–‚ج——R‚حپA [(vپEپق)f](x) = [vپE(پقf)](x)پ@پو(29) ‚إ‚ ‚éژ–‚ئپA vپE[(پقf)(x)] پ@= (ai + bj + ck)پE{[(iپف1 + jپف2 + kپف3)f](x)}پ@پوTEC-0-1-43•â‘«گà–¾—“گشکg“à(8) پ@= (ai + bj + ck)پE{[(i(پف1f) + j(پف2f) + k(پف3f)](x)}پ@پو(19) پ@= (ai + bj + ck)پE{[(پف1f)(x)]i + [(پف2f)(x)]j + [(پف3f)(x)]k}پ@پو(9) پ@= a[(پف1f)(x)] + b[(پف2f)(x)] + c[(پف3f)(x)] پ@= [a(پف1f) + b(پف2f) + c(پف3f)](x)پ@پو(3) پ@= {(ai + bj + ck)پE[i(پف1f) + j(پف2f) + k(پف3f)]}(x)پ@پو(10) پ@= {(ai + bj + ck)پE[(iپف1 + jپف2 + kپف3)f]}(x)پ@پو(19) پ@= [vپE(پقf)](x)پ@پوTEC-0-1-43•â‘«گà–¾—“گشکg“à(8) پˆ vپE[(پقf)(x)] = [vپE(پقf)](x) ‚إ‚ ‚éژ–‚إ‚·پB --- ˆبڈم‚ئ“¯—l‚ج——R‚ة‚و‚ء‚ؤپAپقi ‚ج’è‹`‚ئ‚µ‚ؤTEC-0-1-43•â‘«گà–¾—“گشکg“à(13)‚ًچج—p‚·‚é‚ئپAژں‚ج—l‚ةگ¬‚è‚ـ‚·پB (dri/dt)پEپقiU پك [(dri/dt)پEپقi]U = (dri/dt)پE(پقiU) پEپEپE(32) (dri/dt)پEپقiU(r1, پEپEپE, rn) پ@پك(dri/dt)پE[(پقiU)(r1, پEپEپE, rn)] = {[(dri/dt)پEپقi]U}(r1, پEپEپE, rn) = [(dri/dt)پE(پقiU)](r1, پEپEپE, rn) پEپEپE(33) ‚±‚جژ–‚ئ (پقiU)(r1, پEپEپE, rn) = [i(پف/پفxi) + j(پف/پفyi) + k(پف/پفzi)][U(r1, پEپEپE, rn)]پ@پو TEC-0-1-43•â‘«گà–¾—“گشکg“à(14a) ‚إ‚ ‚éژ–‚©‚çپATEC-0-1-40-29,30‚ج (dri/dt)پEپقiU ‚ًپATEC-0-1-43•â‘«گà–¾—“گشکg“à(13)‚إ’è‹`‚³‚ê‚ؤ‚¢‚é پقi ‚ًژg‚ء‚ؤ‚ج (dri/dt)پEپقiU(r1, پEپEپE, rn) ‚¾پA‚ئ‰ًژك‚µ‚ؤ‚àŒ‹‰ت‚ةچ·‚حڈo‚ـ‚¹‚ٌپB (d/dt)U(r1(t), پEپEپE, rn(t)) = ƒ°i=1n [dri(t)/dt]پE[(پقiU)(r1(t), پEپEپE, rn(t))] پEپEپE(34) 2016.05.16,17,18,20;2019.06.11,12 |
پySEOƒeƒLƒXƒgپz‰F“c—Yˆê03.12.28[–â‘è32]CAN-1-1-15-19,20‚ً“±ڈo‚¹‚وپB“ڑ:d/dt n‡”i=1(mi d/dt ri)=n‡”i=1 mi ri=n‡”i=1(Fi+‡”jپ¸{1,پEپEپE,n}-{i}Fij)=n‡”i=1 Fi+1/2 n‡”i=1‡”jپ¸{1,پEپEپE,n}-{i}(Fij+Fji),=0,=n‡”i=1 Fi[–â‘è33]CAN-1-1-15-27,28‚ً“±ڈo‚¹‚وپB“ڑ:d/dt n‡”i=1(riپ~mi d/dt ri)=n‡”i=1(riپ~mi ri)+n‡”i=1(riپ~mi ri),پ¨0,=n‡”i=1[riپ~(Fi+‡”jپ¸{1,پEپEپE,n}-{i}Fij)]=n‡”i=1(riپ~Fi)+n‡”i=1‡”jپ¸{1,پEپEپE,n}-{i}(riپ~Fij),=1/2 n‡”i=1‡”jپ¸{1,پEپEپE,n}-{i}(riپ~Fij+rjپ~Fji),=(ri-rj)پ~Fij=0[–â‘è34]CAN-1-1-16-9پ`12‚ً“±ڈo‚¹‚وپB“ڑ:d/dt(n‡”i=1 1/2 mi|ri|2+U)=n‡”i=1 miriپEri+n‡”i=1 riپEپقiU