CAN-2-1-5 電磁気学正典 CANONICAL NOTE

CAN-2-1-5

次のページ
前のページ
目次

COM-2-1

[補足説明欄]

1行目の「(5) 線状電流」は、2～11行目の記事のタイトルです。2021.08.20

線状電流の例は、実際問題としては、電線を流れる電流だけです。
しかし、電線を流れる電流では電荷密度がゼロです。
これは、電線中にプラスの電気を持った原子核とマイナスの電気を持った電子の両方が存在し、両者の巨視的な電荷密度の和がゼロだからです。
電荷密度がゼロなのに電流密度が非ゼロに成れるのは、電子が移動するからです。
　

この図では、原子核を赤色の点で、電子を青色の点で表しています。
大多数の電子がいずれかの原子核から受けるクーロン引力のせいでいすれかの原子核から遠ざかり続ける事が出来ないのに対して、残りの少数の電子は移動し続ける事が出来ます。
前者は束縛電子、後者は自由電子と呼ばれます。
ただし、電子に個性は無いという意味では、どの電子も同じ(束縛電子と自由電子は同じ電子)です。
自由電子が自由なのは、自由電子から見れば束縛電子が原子核を覆っている分だけ原子核の電荷が小さく成った様な物であるという要素と、全ての原子核から受けるクーロン力が釣り合う様な位置をたどって渡り歩くという要素によって、理解できるでしょう。
束縛電子と自由電子の巨視的な電荷密度の和の絶対値が原子核の巨視的な電荷密度に等しい為に、巨視的な総電荷密度がゼロに成ります。
もし自由電子の巨視的な電荷密度が変化して巨視的な総電荷密度が少しでもゼロからずれると、クーロン性の強烈な復元力が働いて自由電子の分布は巨視的な総電荷密度が至る所ゼロに成るまで引き戻されます。
この為に自由電子は、全体として非圧縮性流体の様に振る舞い、油圧システムの油の様な働きを電気回路において担います。
自由電子の移動速度が極めて低速なのに、電線を伝わる電気信号の速さが光速に近いのは、その為です。
これはCAN-2-1-4-27の式への反例ではなく、電線を流れる電流でも、微視的にはCAN-2-1-5-13,14の式の多粒子版とCAN-2-1-4-27の式が成り立つのであって、微視的には電荷密度はゼロではありません。
微視的に見ても電荷密度が至る所ゼロならば電流密度も至る所ゼロに成らざるを得ませんが、巨視的な電荷密度がゼロであるだけなら、この様な事が可能なわけです。
CAN-2-1-5-2～11では、荷電物質が微視的に見ても正真正銘の線状連続体である場合を考えています。
つまり、ここに書かれているのは普通の電線を流れる電流の話ではありません。
荷電物質が微視的に見ても正真正銘の線状連続体である場合を考えるなら、その連続体は自身に沿った方向に運動するとは限らないので、電流密度の向きも一般には自身に平行ではなく、「線状電流」というタイトルは不適当です。
「線状電荷」を誤って「線状電流」と書いてしまったようです。2021.08.20,21,22,23,24;2021.09.28;2021.12.03

ここで、予備知識として、ディラックのデルタ関数を、説明しておきます。
デイラックのデルタ関数は
[x ≠ 0 ⇒ δ(x) = 0] and ∫_-∞^∞ dx δ(x) = 1 ・・・ (d1)
という条件で定義される実1変数実数値関数δの事だ、と普通言われます。
しかし、[x ≠ 0 ⇒ δ(x) = 0] なら ∫_-∞^∞ dx δ(x) = 1 は不可能です。
もっと言うと、δが連続関数で[x ≠ 0 ⇒ δ(x) = 0]なら[x = 0 でも δ(x) = 0]つまり[全てのxに対して δ(x) = 0]に成ってしまいます。
だからデルタ関数は普通の関数としては存在し得ません。
この事も周知の事実です。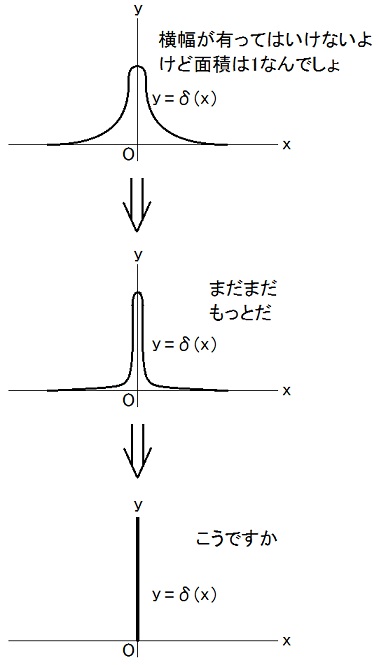
　

そこで、任意関数fに対して
∫_-∞^∞ dx f(x)δ(x) = f(0) ・・・ (d2)
に成る事に着目して、関数fを数f(0)に写す写像(汎関数)がデルタ関数(関数ではなく汎関数なのだけれど)なのだ、という風に定義の厳密化が行なわれるのが、数学では普通です。
デルタ関数を案出したディラック(Dirac)は物理学者であり、物理学ではデルタ関数を厳密化せずに普通の関数であるかの様に扱うのが普通ですが、数学ではそれは許されない様です。
デルタ関数の厳密化の私のやり方は、(d2)に依拠する方法とは少し違っていて、以下の様に考えます。
例えば、(d/dx)f(x) = δ(x) という式は a ＜ 0 ＜b ⇒ f(b) - f(a) = 1 である事を意味する、と考えます。
デルタ関数自体に汎関数としてのなどの厳密な定義を与えるのではなく、デルタ関数を含む式に厳密な定義を与える、それが私のやり方です。
デルタ関数は、その様に厳密な定義を与える事が出来る式に含まれる形でしか現れない、からです。
このやり方を私は、自著「古典物理学」を執筆する過程で編み出しました。
位置xでの電荷密度がqδ³(x - a)であるとは、任意の空間領域Vについて、a ∈ V ならばV内に有る電荷はqでありかつnot(a ∈ V) ならばV内に有る電荷は0である事、を無理矢理「密度」という言葉を使って表現した物だ、と考えます。
数学の人よ、もしここを御覧になっていたら、この私の厳密化法で、超関数の理論を書き換えてみたらいかがでしょうか。
例えば、集合を変数とする関数Qを考え、この関数が不連続である、とするわけです。
Q(V) を ∫_V d³x ρ(x) に見立てて、a ∈ V ⇒ Q(V) = q, not(a ∈ V) ⇒ Q(V) = 0.
デルタ関数についての私の考え方はそうですが、当典では、物理学で普通行なわれる様に、デルタ関数を普通の関数であるかの様に扱います。
ここで厳密化の話をしたのは、デルタ関数を普通の関数であるかの様に定義する条件が厳密には矛盾を含んでいるからと言って、その条件を形式的に運用して得られた結果が無根拠である事には成らない、という事情を説明するためです。
デルタ関数を普通の関数であるかの様に扱って書かれた証明は、厳密な証明の粗筋の略記であって、それは対応する厳密な証明が存在する事を示唆する、と解釈するのが順当でしょう。
以下では、(d1)ではなく(d2)と
δ(x) = δ(-x) ・・・ (d3)
の両方が成り立つ事をデルタ関数の定義とします。
デルタ関数の定義から導き出される公式を以下に列挙しておきます。
Dδ(0) = 0 ・・・ (d4),
∫_-∞^∞ dx f(x)δ(x - a) = f(a) ・・・ (d5),
f(x)δ(x - a) = f(a)δ(x - a) ・・・ (d6),
δ(f(x)) = δ(x - f^-1(0))/|Df(f^-1(0))| ・・・ (d7),
f(x) = 0 の解が複数有る場合には例えば f(a_k) = 0 (k = 1, 2, 3, ・・・) ならば、δ(f(x)) = Σ_k δ(x - a_k)/|Df(a_k)| ・・・ (d7a).
デルタ関数の表現としては、例えば、以下の表現が使われる事が有ります。
δ(x) = lim_p→∞ [√(p/π)]exp(-px²) ・・・ (d8),
δ(x) = lim_p→∞ [sin(px)]/(πx) ・・・ (d9),
δ(x) = [1/(2π)]∫_-∞^∞ dp exp(ipx) ・・・ (d10).
(d4)(d7)(d7a)で使われているDは、TEC-0-1-43の補足説明欄の赤枠内で説明されている微分演算子です。
(d9)は、pを大きくするに従がってx軸方向の単位長さ当たりの皺(しわ)の数が増え x = 0 でのyの値も増えますが、|y|の極大値は全て大雑把に言って |y| = 1/|πx| に沿った所に有る(図の破線はその様子)ので、pが変化してもグラフの横幅は概略としては変化しません。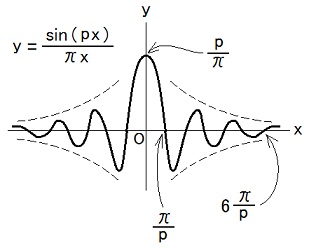
　

x軸方向の単位長さ当たりの皺の数が増えると、f(x)を掛けてxで積分する時に、x = 0 付近以外では隣り合う山と谷の効果が相殺して積分への寄与が発生しなくなります(d9a)。
横幅が残るので、これをデルタ関数の表現として正当だとして良いのか否かは、権威への信用に頼らず自分の鑑識眼だけで判断したのでは、私でも自信を持って答える事が出来ません。
しかし、結論を言えば、この表現もデルタ関数の表現として正当です。
ただし、科学においては、究極的には本当は何でも自分の鑑識眼だけで判断しなければならず、権威への信用はそのヒントに過ぎない、という道理が、それよりもっと優先度の高い道理である事は、変わりません。
勉強を続けて行くと後々身の回りの生活用品の様に多用される事に成る(d10)の根拠が(d9)であり、(d9)の根拠には百パーセントは自信を持てない、この辺りから、物理学の学習も研究も「ホントこれで合ってるのかなあ？」と心配しながら進めて行く領域に入ります。
この様な領域で真偽を判断するには、考えられる批判の各々が言葉尻への批判に過ぎないのかそれとも主旨への批判なのかを嗅ぎ分ける、デルタ関数以前よりいっそう高度な鑑識眼が必要に成ります。
日本物理学会2006年春季大会＠学会発表＠活動報告＠学問＠宇田英才教室の冒頭に、この種の議論の実例が書かれています。
(d2)と(d3)がデルタ関数の定義なんだから(d9)に不明な点は全然ないんだよ、と言うなら、それじゃあ「波長の極端に短い電波はほとんど無いのと同じだ、いやあ汎関数だからね」と言われたらどうするんだろうか。
また、(d8)(d9)を使う時には、p → ∞ という極限操作を取らずに必要な計算をして、計算が終わった後でp → ∞ という極限操作を取る必要が有ります。
この点も、(d8)(d9)が額面通りには成り立たない式である事を意味します。
(d7)でf^-1はfの逆写像です。つまりf(f^-1(y)) = y.
例えば f(x) = ax and a≠0 の場合には Df(x) = a, f^-1(0) = 0 だから δ(ax) = δ(x - 0)/|a|.
∴ δ(ax) = δ(x)/|a| ・・・ (d7b)
f(x) = c(x - a)(x - b) なら Df(x) = c(x - a) + c(x - b), f(a) = f(b) = 0 だから、(d7a)に a₁ = a, a₂ = b を代入して、
δ(c(x - a)(x - b)) = [δ(x - a) + δ(x - b)]/|c(a - b)| ・・・ (d7c).
さて、
δ(x¹)δ(x²)δ(x³) を δ³(x) と書く慣習があります。
(x¹, x², x³) と (x'¹, x'², x'³) が x¹ = x¹(x'¹, x'², x'³), x² = x²(x'¹, x'², x'³), x³ = x³(x'¹, x'², x'³) という座標変換で結ばれており、x = a の時 x' = a' だとすると、
||∂(x'¹, x'², x'³)/∂(x¹, x², x³)||δ³(x' - a') = δ³(x - a) ・・・ (d11).
ただし |∂(x'¹, x'², x'³)/∂(x¹, x², x³)| は、座標変換のヤコビアンであり、(j, k)成分が∂x'^j/∂x^kである行列の行列式です。
|∂(x'¹, x'², x'³)/∂(x¹, x², x³)| = Σ_p=1³Σ_q=1³Σ_r=1³ ε^pqr(∂x'¹/∂x^p)(∂x'²/∂x^q)(∂x'³/∂x^r).
ε^pqrは、TEC-0-2-1-11,12で説明されているレビチビタの反対称テンソルです。
||∂(x'¹, x'², x'³)/∂(x¹, x², x³)|| はヤコビアンの絶対値です。
ここからは、ここまでの式の根拠を書きます。
Dδ(0) = (1/2)[Dδ(0) + Dδ(0)] = (1/2)[(d/dx)δ(x) - (d/dx)δ(-x)]_x=0 = (1/2){(d/dx)[δ(x) - δ(-x)]}_x=0 = 0 ∵ (d3).
これが(d4)の根拠です。
x' = x - a と置く置換積分を使うと、
∫_-∞^∞ dx f(x)δ(x - a) = ∫_-∞^∞ dx' f(x' + a)δ(x') = f(0 + a) = f(a).
これが(d5)の根拠です。
任意関数gに対して、
∫_-∞^∞ dx g(x)f(x)δ(x - a) = g(a)f(a) = ∫_-∞^∞ dx g(x)f(a)δ(x - a).
これが(d6)の根拠です。
x' = f(x) と置く置換積分を考えれば、任意関数gに対して、
∫_-∞^∞ dx g(x)δ(f(x)) = ∫_-∞^∞ dx' g(f^-1(x'))δ(x')/|dx'/dx| = ∫_-∞^∞ dx' g(f^-1(x'))δ(x')/|Df(f^-1(x'))| = g(f^-1(0))/|Df(f^-1(0))|
　= ∫_-∞^∞ dx g(x)δ(x - f^-1(0))/|Df(f^-1(0))|.
これが(d7)の根拠です。
x ≠ 0 ⇒ lim_p→∞ [√(p/π)]exp(-px²) = 0 ・・・ (d8a),
p ＞ 0 ⇒ ∫_-∞^∞ dx [√(p/π)]exp(-px²) = 1 ・・・ (d8b).
これが(d8)の根拠です。
(d8b)の根拠は以下です。
[∫_-∞^∞ dx exp(-px²)]² = ∫_-∞^∞ dx exp(-px²)∫_-∞^∞ dy exp(-py²) = ∫_-∞^∞ dx∫_-∞^∞ dy exp[-p(x² + y²)]
　= ∫₀^2π dθ∫₀^∞ dr r exp(-pr²) ・・・ x = r cosθ, y = r sinθ と置いた
　= 2π∫₀^∞ dr r exp(-pr²) = 2π[-(1/(2p))exp(-pr²)]₀^∞ = π/p.
この事と ∫_-∞^∞ dx exp(-px²) ≧ 0 [∵ exp(-px²) ≧ 0] である事から、
∫_-∞^∞ dx exp(-px²) = √(π/p).
ここまでが(d8b)の根拠です。
p ＞ 0 ⇒ ∫_-∞^∞ dx [sin(px)]/(πx) = 1 ・・・ (d9b)
である事と(d9a)が(d9)の根拠です。
lim_L→∞∫_-L^L dp exp(ipx) = lim_L→∞∫_-L^L dp [cos(px) + i sin(px)] = lim_L→∞ [(1/x)sin(px) - (i/x)cos(px)]_p=-L^L = 2lim_L→∞ (1/x)sin(Lx).
この事と(d9)が(d10)の根拠です。
これを見れば分かる様に、(d10)における積分∫_-∞^∞ dp は lim_L→∞∫_-L^L dp でなければいけません。
積分範囲の下端と上端を独立に-∞と∞に近付けたのでは、(1/x)cos(px)の項が効いてしまい、(1/x)cos(px) は x = 0 の付近に限ってもxでの積分値が定まりません。
従がって、(d10)は(d9)にも増してきわどいと言えます。
だから私は、何かやっていてつまづくと、(d10)を濫用してしまったからではないかも疑いますが、実際にそうだった事は一度も有りません。
(d11)の根拠は、CAN-2-1-4-27への補足説明の(7)の根拠と同様です。
(d9b)の導出は、複素変数関数の積分を使って行ないます。
z = x + iy として、(1/z)exp(iz)を下図の閉曲線に沿って1周線積分した結果はゼロに成ります(d9b1)。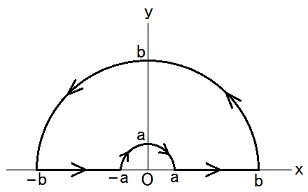
　

0 = ∫_a^b dx (1/x)exp(ix) + ∫_θ=0^π d(b cosθ + ib sinθ)・[1/(b cosθ + ib sinθ)]exp[i(b cosθ + ib sinθ)]
　　+ ∫_-b^-a dx (1/x)exp(ix) + ∫_θ=π⁰ d(a cosθ + ia sinθ)・[1/(a cosθ + ia sinθ)]exp[i(a cosθ + ia sinθ)]
　= ∫_a^b dx (1/x)exp(ix) + ∫₀^π dθ[(-sinθ + i cosθ)/(cosθ + i sinθ)]exp[i(b cosθ + ib sinθ)]
　　+ ∫_-b^-a dx (1/x)exp(ix) + ∫_π⁰ dθ[(-sinθ + i cosθ)/(cosθ + i sinθ)]exp[i(a cosθ + ia sinθ)] ・・・ (d9b2)
このうちの2番目の積分は b → ∞ でゼロに近付く(d9b3)し、
∫_-b^-a dx (1/x)exp(ix) = ∫_a^b dx' (-1/x')exp(-ix') ・・・ x' = -x と置いた
だから、(d9b2)で a → +0, b → ∞ と置く事によって、
0 = ∫₀^∞ dx (1/x)[exp(ix) - exp(-ix)] + ∫_π⁰ dθ[(-sinθ + i cosθ)/(cosθ + i sinθ)]
∴ ∫₀^∞ dx (1/x)[exp(ix) - exp(-ix)] = ∫₀^π dθ(-sinθ + i cosθ)(cosθ - i sinθ)] = πi ・・・ (d9b4)
∵ (-sinθ + i cosθ)/(cosθ + i sinθ) = (-sinθ + i cosθ)(cosθ - i sinθ) = i ・・・ (d9b5).
だと分かります。
(d9b4)と sin x = [exp(ix) - exp(-ix)]/(2i) から、
∫₀^∞ dx (1/x)sin x = π/2
この事と (1/x)sin x が奇関数である事から、
∫_-∞^∞ dx (1/x)sin x = π
∴ ∫_-∞^∞ dx (1/x)sin(px) = ∫_x'=-∞^∞ (dx'/p) (p/x')sin(x') = ∫_-∞^∞ dx' (1/x')sin(x') = π ・・・ x' = px と置いた
これが(d9b)の根拠です。
(d9b3)の根拠は以下です。
|∫₀^π dθ[(-sinθ + i cosθ)/(cosθ + i sinθ)]exp[ib(cosθ + i sinθ)] |
= | i∫₀^π dθ exp[ib(cosθ + i sinθ)] |　∵ (d9b5)
= |∫₀^π dθ exp[ib(cosθ + i sinθ)] |
≦ ∫₀^π dθ |exp[ib(cosθ + i sinθ)]|　∵ 三角不等式
= ∫₀^π dθ exp(-b sinθ)
= 2∫₀^π/2 dθ exp(-b sinθ)
≦ 2∫₀^π/2 dθ exp(-2bθ/π)　∵ sinθ ≧ 2θ/π ≧ 0
= (π/b)(1 - e^-b)
＜ π/b.
　

ここまでしなくても、0 ＜ θ ＜ π では b → ∞ で exp(-b sinθ) → 0 だから b → ∞ で ∫₀^π dθexp(-b sinθ) → 0 なんだ、という論法でも物理学では許されます。
この論法は数学的にも厳密に正しいかもしれませんが、b → ∞ での exp(-b sinθ) → 0 という収束が一様収束でなければ b → ∞ で ∫₀^π dθ exp(-b sinθ) → 0 とは成らない可能性を心配したので私は、∫₀^π dθ exp(-b sinθ) ＜ π/b という不等式を示す事にしました。
(d9b1)の根拠は以下です。
z = x + i y, f(z) = u(x, y) + i v(x, y), fは解析的であるとすると、
f(z) dz = [u(x, y) + i v(x, y)](dx + i dy) = [u(x, y) dx - v(x, y) dy] + i[v(x, y) dx + u(x, y) dy]
だから、曲線Cに沿った∫_C dz f(z) は [u(x, y)]i + [-v(x, y)]j と [v(x, y)]i + [u(x, y)]j という2つの実ベクトル場の線積分に還元されます。
ところが、fが解析的であるとは、コーシー・リーマン方程式:
∂u(x, y)/∂x = ∂v(x, y)/∂y and ∂u(x, y)/∂y = -∂v(x, y)/∂x
が成り立つ事だから、fが解析的ならば、これら2つのベクトル場はどちらも渦無しである事に成ります。
渦無しならば、ストークスの定理(下の青枠内で説明されている)によって、閉曲線に沿った1周線積分は2つのベクトル場のどちらについてもゼロに成ります。
この様に複素解析関数を複素平面内の閉曲線に沿って1周線積分するとゼロに成る事、をコーシー・グルサの定理と呼びます。
f(z) = (1/z)exp(iz) = [1/(x + iy)]exp[i(x + iy] = [(x - iy)/(x² + y²)]e^-y(cos x + i sin x)
　= [e^-y/(x² + y²)][(x cos x + y sin x) + i(x sin x - y cos x)]
の場合には、
u(x, y) = [e^-y/(x² + y²)](x cos x + y sin x), v(x, y) = [e^-y/(x² + y²)](x sin x - y cos x)
だから、
∂u(x, y)/∂x = -2x[e^-y/(x² + y²)²](x cos x + y sin x) + [e^-y/(x² + y²)](cos x - x sin x + y cos x)
　= [e^-y/(x² + y²)²][(y² - x²)cos x + y(x² + y²)cos x -2xy sin x - x(x² + y²)sin x],
∂u(x, y)/∂y = [-1 - 2y/(x² + y²)][e^-y/(x² + y²)](x cos x + y sin x) + [e^-y/(x² + y²)]sin x
　= [e^-y/(x² + y²)²][-x(x² + y²)cos x - 2xy cos x -y(x² + y²)sin x + (x² - y²)sin x],
∂v(x, y)/∂x = -2x[e^-y/(x² + y²)²](x sin x - y cos x) + [e^-y/(x² + y²)](sin x + x cos x + y sin x)
　= [e^-y/(x² + y²)²][(y² - x²)sin x + 2xy cos x + x(x² + y²)cos x + y(x² + y²)sin x],
∂v(x, y)/∂y = [-1 - 2y/(x² + y²)][e^-y/(x² + y²)](x sin x - y cos x) + [e^-y/(x² + y²)](- cos x)
　= [e^-y/(x² + y²)²][y(x² + y²)cos x + (y² - x²)cos x - x(x² + y²)sin x -2xy sin x].
と成り z ≠ 0 ではコーシー・リーマン方程式が成り立ちます。

//2021.09.07-28;2021.12.04,05,06,07,08

曲面Sの外周が閉曲線Cであるとし、Sの内部を左手に見ながらCに沿ってCの向きに歩く人の足から頭に向かう向きがSの裏から表に向かう向きに成る様にSの表裏とCの向きを定め、vをベクトル場とする時、
∫_S dS・∇×v(x) = ∫_C dx・v(x) ・・・ (s1).
これをストークスの定理と呼びます。
Sを面素片に分割した時、各面素片の外周についてのvの線積分を全ての面素片にわたって足すとCについてのvの線積分に成る(外周以外の線積分はキャンセルする)
　

ので、ストークスの定理はSが無限小の場合に成り立てばSが有限の場合にも成り立つ、と分かります。
∫_S(k) dS_k・∇×v(x) = ∫_C(k) dx・v(x)
　⇒ ∫_S dS・∇×v(x) = Σ_k∫_S(k) dS_k・∇×v(x) = Σ_k∫_C(k) dx・v(x) = ∫_C dx・v(x) ・・・ (s2).
上の図は平面内に描かれていますが、外周以外の線積分がキャンセルするという事情は、Sが曲面であっても、この図と同様です。
特別な場合として、Sがx³軸に垂直な平面内に在り、x³軸の正の向きがSの裏から表に向かう向きである場合を考えると、
(idx¹ + jdx²)・[iv¹(x) + jv²(x) + kv³(x)] = (dx¹)v¹(x) + (dx²)v²(x) = (idx² - jdx¹)・{iv²(x) + j[-v¹(x)]} ・・・ (s3)
であり、ガウスの定理(※1)によって、
∫_C (idx² - jdx¹)・{iv²(x) + j[-v¹(x)]} = ∫_S dx¹dx² {(∂/∂x¹)v²(x) + (∂/∂x²)[-v¹(x)]} ・・・ (s4)
だから(s3)(s4)より、
∫_C (idx¹ + jdx²)・[iv¹(x) + jv²(x) + kv³(x)] = ∫_S dx¹dx² [(∂/∂x¹)v²(x) - (∂/∂x²)v¹(x)] ・・・ (s5)
と成りますが、
(∂/∂x¹)v²(x) - (∂/∂x²)v¹(x) = k・[∇×v(x)] ・・・ (s6)
だから、dx = idx¹ + jdx², v(x) = iv¹(x) + jv²(x) + kv³(x), dS = kdx¹dx² である事に注意すれば、(s5)(s6)から、
∫_C dx・v(x) = ∫_S dS・[∇×v(x)] ・・・ (s1)
だと分かります。
これはどの直交右手系でも成り立つので、Sが平面内に在る場合には、その平面がx³軸に垂直でなくても、その平面がx'³軸に垂直である様なx'¹-x'²-x'³系で考えれば、やはり(s1)が成り立つと分かります(※2)。
Sが無限小である場合にはSは平面内に在るとしてよいので、Sが無限小ならば(s1)が成り立つと分かります。
この事と(s2)から、Sが有限でも(s1)が成り立つと分かります。
※1. ガウスの定理はTEC-0-2-3の補足説明欄で説明されています。
そこに書かれているのは3次元の場合のガウスの定理ですが、ここで使ったのは2次元の場合のガウスの定理です。
2次元の場合には、x¹-x²平面内の面Sの外周をCとし、iu¹(x¹, x²) + ju²(x¹, x²) をベクトル場とする時、ガウスの定理は、
∫_C (idx² - jdx¹)・[iu¹(x¹, x²) + ju²(x¹, x²)] = ∫_S dx¹dx² [∂₁u¹(x¹, x²) + ∂₂u²(x¹, x²)] ・・・ (s7)
という風に書けます。
この事は、idx² - jdx¹ が idx¹ + jdx² に垂直で長さが|idx¹ + jdx²|に等しくSの内から外に向かう向きなので idx² - jdx¹ は3次元の場合のガウスの定理におけるdSに相当する、という事に注意すれば分かります。
(s4)では、u¹ = v², u² = -v¹ の場合を考えています。
※2. 座標系非依存という言葉が、CAN-1-1-27-12,13への補足説明の中で説明されています。
これを、(s1)の場合に即して以下に説明します。
x¹-x²-x³系とx'¹-x'²-x'³系が x = x¹, y = x², z = x³ とした時のCAN-1-1-8-12～18の関係で結ばれているならば、
dx^j = Σ_n=1³ R_jndx'ⁿ ・・・ (s8)
であるだけでなく、
iv¹(x) + jv²(x) + kv³(x) = i'v'¹(x') + j'v'²(x') + k'v'³(x') ・・・ (s9)
である様な v'¹, v'², v'³ は、v¹, v², v³ と、
v^j(x) = Σ_k=1³ R_jkv'^k(x') ・・・ (s10)
という関係で結ばれる事が分かります。(CAN-1-1-8-5,6,12,13,14からCAN-1-1-8-16,17,18が導かれるのと理由は同じ)
したがって、(s8)(s10)から、
Σ_j=1³ (dx^j)v^j(x) = Σ_j=1³ Σ_n=1³ Σ_k=1³ R_jn(dx'ⁿ)R_jkv'^k(x') = Σ_n=1³ Σ_k=1³ δ_nk(dx'ⁿ)v'^k(x') = Σ_k=1³ (dx'^k)v'^k(x') ・・・ (s11)
∵ Σ_j=1³ R_jnR_jk = δ_nk (TEC-0-1-16-1,2).
だから∫_C dx・v(x) は x¹-x²-x³系で計算してもx'¹-x'²-x'³系で計算しても結果が同じに成ります。
この事を、∫_C dx・v(x) は座標系非依存だ、と言います。
一方、CAN-2-1-2-16～19への補足説明に注意しながら、CAN-1-1-27-18への補足説明に書かれている略記法を使うと、
ε^jkn∂_kvⁿ(x) = ε^jkn(∂/∂x^k)vⁿ(x) = ε^jknR_nq(∂x'^p/∂x^k)(∂/∂x'^p)v'^q(x')　∵ (s10)
　= ε^jknR_nqR_kp(∂/∂x'^p)v'^q(x')　∵ x'^p = (R^-1)_pk x^k = (R^t)_pk x^k = R_kp x^k　∵ CAN-1-1-8-15～18
　= R_jsε^spq(∂/∂x'^p)v'^q(x') ・・・ (s12)
∵ε^jknR_kpR_nq = R_jsε^spq ・・・ (s13).
だから、CAN-1-1-8-5,6,12,13,14からCAN-1-1-8-16,17,18が導かれるのと同じ理由で、(s12)から下式が導かれます。
iε^1kn(∂/∂x^k)vⁿ(x) + jε^2kn(∂/∂x^k)vⁿ(x) + kε^3kn(∂/∂x^k)vⁿ(x)
　= i'ε^1kn(∂/∂x'^k)v'ⁿ(x') + j'ε^2kn(∂/∂x'^k)v'ⁿ(x') + k'ε^3kn(∂/∂x'^k)v'ⁿ(x') ・・・ (s14).
この事を、∇×v(x) は座標系非依存だ、と言います。
したがって、dS = (dx'¹)(dx'²)k' として
∫_S dS・[∇×v(x)] = ∫_S dx'¹dx'² k'・[iε^1kn∂_kvⁿ(x) + jε^2kn∂_kvⁿ(x) + kε^3kn∂_kvⁿ(x)]
とした結果は、
∫_S dx'¹dx'² k'・[i'ε^1kn∂_kv'ⁿ(x') + j'ε^2kn∂_kv'ⁿ(x') + k'ε^3kn∂_kv'ⁿ(x')]
= ∫_S dx'¹dx'² ε^3kn∂_kv'ⁿ(x')
= ∫_S dx'¹dx'² [(∂/∂x'¹)v'²(x') - (∂/∂x'²)v'¹(x')]
に一致する事が(s14)から言えます。(∂_kについてTEC-0-1-43補足説明欄赤枠内の説明を参照して下さい)
この事を、(s1)は座標系非依存だ、と言います。
(s13)は、2つのベクトルを回転した後で外積しても外積した後で回転しても結果は変わらない、というCAN-1-1-28-18への補足説明でも書いた理屈の言い換えです。
(s13)は、次の様にして証明されます。
R ∈ SO(3) だから、+1 = |R| = ε^jknR_j1R_k2R_n3 (CAN-1-1-22-19への補足説明、TEC-0-2-1-11,12)
この事と、行列の3つの列が全て異ならなければ行列式はゼロに成る事、および行列の列を入れ替えると行列式の符号が変わる事から、
ε^jknR_jsR_kpR_nq = ε^spq
だと分かります。
この事と R_rsR_js = δ_rj である事(∵CAN-1-1-8-15)から、
R_rsε^spq = ε^jknR_rsR_jsR_kpR_nq = ε^jknδ_rjR_kpR_nq = ε^rknR_kpR_nq.
証明終わり。
俗説では、右脳と左脳が二者択一の様に対比されて、右脳を利かせた思考は左脳を利かせた思考より優れている、左脳ではなく右脳を使え、という風に吹聴される傾向が有ります。
しかし、学問の研究のレベルでは、右脳と左脳を両方とも活用する二刀流は普通の事です。
両方とも活用すれば勝てるのではなく、両方とも活用しなければ負ける、というのが学問の研究のレベルです。
その意味で、左脳で考えず右脳で考えろという通俗アドヴァイスは間違っており、この間違いは、後天的な努力が優れているタイプと先天的な才能が優れているタイプに優勝候補を分類する通俗コメントが間違っているのと同じです。
優勝には努力と才能の両方が必要なものだからです。
(s13)を回転と外積が交換する事だと画像で認識するのは右脳的で、(s13)という数式として認識するのは左脳的だと言えます。
視覚的判断は右脳に、言語的判断は左脳に属する、のでしょう。
まず、どういう定理が何故成り立つはずかを右脳で判断し、それをガイドに証明は左脳で行なう、という良い例に(s13)は成っています。
一般論としては、左脳で進めない所は右脳で進み、右脳で進めない所は左脳で進む、そうした後で、左脳で進んだ部分は右脳語に、右脳で進んだ部分は左脳語に翻訳しておくのです。
すると次からは、翻訳を見れば、左脳で進めなかった所も左脳で進めるし、右脳で進めなかった所も右脳で進める様に成るわけです。
さて、ここまでで私は、コーシー・グルサの定理をストークスの定理に還元し、ストークスの定理をガウスの定理に還元する、というやり方で説明を進めて来ましたが、これは、学術的なオリジナリティには至らないまでも解説法としては新しいはずです。
従来の解説法では、これら3つの定理が別の科目や同じ科目の別の単元で全く別の話として別々に解説されるのが伝統の轍に成っています。
それに対して私の解説法は、分量が少なくて読むのが楽だし、関連性が分かる点で学習到達点も従来より高いものです。
当典の執筆まで含めて私のやっている事を、お前は悪い事をしている、という意味の言葉で誹謗中傷する人が多いけれど、どうでしょう皆さん、コーシー・グルサの定理とストークスの定理についての私のこの解説記事、世の中に存在しない方が良いですか？
そんなわけありませんよね。
しかし悪い事だからやめなければいけないなら、この記事は世の中に存在しないんですよ。
学問の名において「その方が良いんだ」と言ってる連中は一体どういう了見なのでしょうか。

//2021.09.25,28,29;2021.10.01;2021.12.10,12,15

3, 4行目について。
まず、記号法を改定しておきます。
σは線状連続体の部位を指示するパラメータだとし、線状連続体の時刻tにおける位置のパラメータ表示を、
(x¹, x², x³) = (ξ¹(σ, t), ξ²(σ, t), ξ³(σ, t)) つまり x = ξ(σ, t) とします。
さらに、時刻tにおける部位σの電荷線密度をρ'(σ, t)とし、時刻tにおける部位σの速度をu'(σ, t)とします。
u(ξ(σ, t), t) = u'(σ, t) ・・・(1),
u'(σ, t) = ∂ξ(σ, t)/∂t ・・・(2).
すると、電荷密度と電流密度は以下の式で表されます。

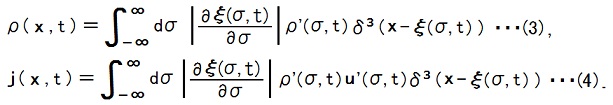
ところが
ξ(σ, t) ∈ V ⇒ ∫_V d³x δ³(x - ξ(σ, t)) = 1,
not[ξ(σ, t) ∈ V] ⇒ ∫_V d³x δ³(x - ξ(σ, t)) = 0
だから、
∫_V d³x ρ(x, t) = ∫_{ξ(σ, t) ∈ V} dσ |∂ξ(σ, t)/∂σ|ρ'(σ, t)
である事を(3)は意味し、これはρ'とρが線密度と3次元密度の関係に成っている事を意味します。
3行目の式は(3)に変更されますが、4行目の式はそのまま成り立ちます。
u(x, t)δ³(x - ξ(σ, t)) = u(ξ(σ, t), t)δ³(x - ξ(σ, t)) = u'(σ, t)δ³(x - ξ(σ, t))
だからです。
24日＠2019年12月＠日記＠宇田英才教室で紹介されている2ch記事に、3行目の式は間違っているのではないか、という問題についての討論が含まれます。
プロレスラーの木村花さんの死をキッカケに「ネットでの誹謗中傷」という言葉で2020年頃に問題意識が社会的に高まった攻撃をそこで私は受けていますが、攻撃者が極めて早期に3行目の式に目を付けている事は、何でもいいから確実に間違っている点をひとつ見付け出しそれによって物理学正典の全体を信用されなくしようという方針を攻撃者が取っている表れだと思われます。2021.08.31;2021.09.01,02,06,07;2021.12.17

6,7行目の式は間違っています。
正しくは以下の様に考えます。
電荷保存則は、任意のa, bに対して

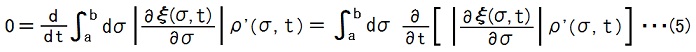
が成り立つ事だ、と考えられます。
(5)は、線状連続体の部分 a ＜ σ ＜ b の電荷は時間が経っても変化しない、という意味です。
a, bは任意だから、

ただし、n'(σ, t) ≡ [∂ξ(σ, t)/∂σ]/|∂ξ(σ, t)/∂σ| ・・・(7)
つまり、線状連続体の部位σでの単位接線ベクトルを n'(σ, t) と書く事にしました。
特に、σが線状連続体に沿った長さに一致している瞬間には、|∂ξ(σ, t)/∂σ| = 1 だから、

これは9,10行目の式と食い違っています。
だから、9,10行目の式は間違っています。
ただし、9,10行目では ∂ρ'(σ, t)/∂t を dρ'/dt と書いています。
さらに、Vを空間領域とし、Vの境界面(内が裏、外が表)をSとし、時刻tには σ = a(t) と σ = b(t) で線状連続体とSが交差しているとすると、つまり、線状連続体の部分 a(t) ＜ σ ＜ b(t) がVの内部に存在し、部分 σ ＜ a(t) と部分 σ ＞ b(t) がVの外部に存在する瞬間を考えると、

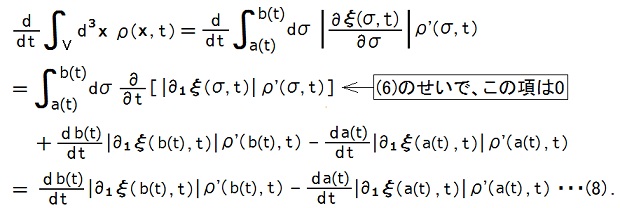
ところが、線状連続体とSの交点は時間が経ってもS上に存し続けるので、S = {x |f(x) = const.} とすると、

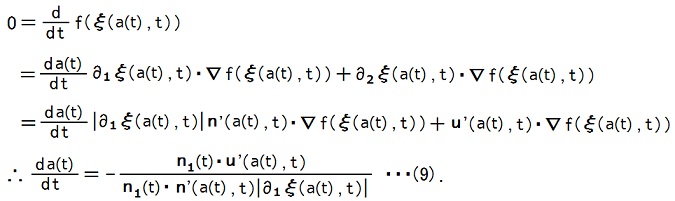
ただし、n₁(t) ≡ ∇f(ξ(a(t), t))/|∇f(ξ(a(t), t))| ・・・(10)
つまり n₁(t)は x = ξ(a(t), t) でのSの単位法線ベクトルだ、としました。
同様にして、

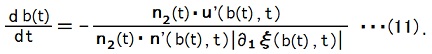
である事が分かります。
n₂(t) ≡ ∇f(ξ(b(t), t))/|∇f(ξ(b(t), t))| ・・・(12).
(9)(11)を(8)に代入すると、

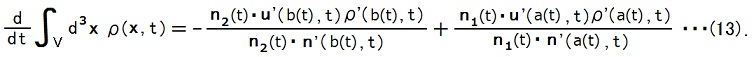
一方、デルタ関数の性質を使えば、(4)から、

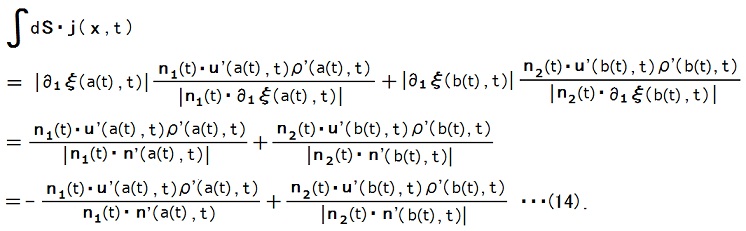
ここで、n'(a(t), t)はSの表から裏に向かうベクトルであり、n'(b(t), t)はSの裏から表に向かうベクトルである事を使いました。
n₁(t)・n'(a(t), t) ＜ 0, n₂(t)・n'(b(t), t) ＞ 0.
(13)(14)から、確かにCAN-2-1-4-18,19の式が成り立っている事が分かります。
したがって、電荷保存則が(5)で表される、という見当は正解でした。
この事は、CAN-2-1-4-27の式と絶縁体の定義の両方が成り立つ事がCAN-2-1-4-23,24の式の十分条件である事の具体例です。
(14)のうちのデルタ関数の性質を使う部分は次の様に考えます。
例えば V = {x| c₁ ≦ x³ ≦ c₂}, ∂ξ³(σ, t)/∂σ ＞ 0 の場合には、
S = {x| x³ = c₁ or x³ = c₂}, n₁(t) = -k, n₂(t) = k, ξ³(a(t), t) = c₁, ξ³(b(t), t) = c₂ だから、

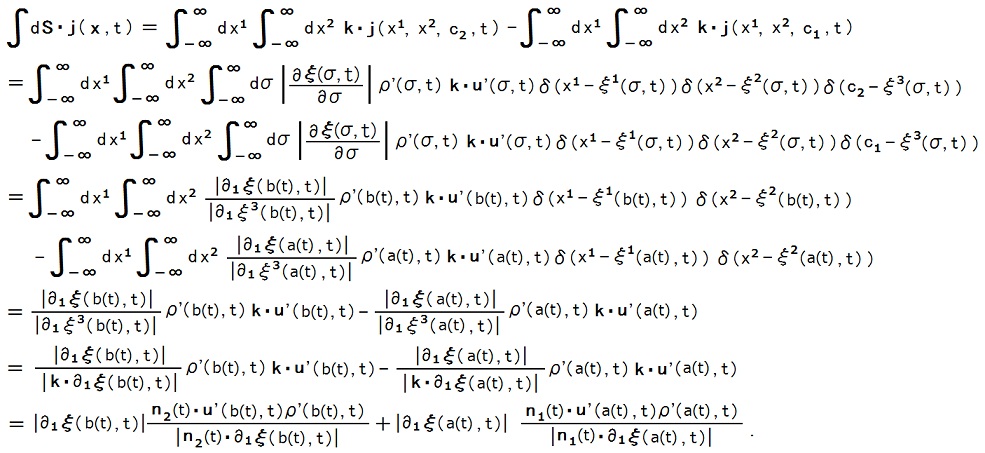
この考え方をSが曲面である場合に一般化すれば分かります。
Sが曲面である場合を考えるに当たって、以下の条件を満たす曲線座標系 x'¹-x'²-x'³ とベクトル値関数ξ'を導入します。
x¹ = x¹(x'¹, x'², x'³), x² = x²(x'¹, x'², x'³), x³ = x³(x'¹, x'², x'³) つまり x = x(x').
この逆変換を x'¹ = x'¹(x¹, x², x³), x'² = x'²(x¹, x², x³), x'³ = x'³(x¹, x², x³) つまり x' = x'(x) だとしておきます。
ξ(σ, t) = x(ξ'(σ, t)) つまり x'¹-x'²-x'³系での線状連続体の位置のパラメータ表示は x' = ξ'(σ, t).
j ≠ k ⇒ [∂_j x(ξ'(b(t), t))]・ [∂_k x(ξ'(b(t), t))] = 0 ・・・下図の3本の黒実線は x = ξ(b(t), t) で直交している。
[∂₁ x(ξ'(b(t), t))]×[∂₂ x(ξ'(b(t), t))] はSの裏から表に向かうベクトルである(逆ならx'¹とx'²を入れ替えるだけでこう出来ます)。
S = {x(x')| x'³ = ξ'³(b(t), t)} ・・・ Sは x'³ = const. 面である。
∇x'³(x) はSの裏から表に向かうベクトルである(逆なら -x'³ をx'³と定め直すだけでこう出来ます)。

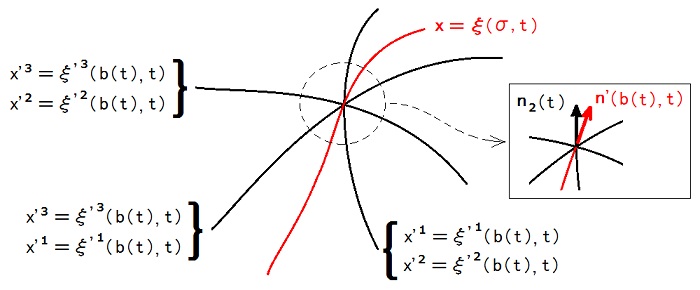
すると、
|∂(x¹, x², x³)/∂(x'¹, x'², x'³)|δ³(x - ξ(σ, t)) = δ³(x' - ξ'(σ, t)) = δ(x'¹ - ξ'¹(σ, t))δ(x'² - ξ'²(σ, t))δ(x'³ - ξ'³(σ, t)).
したがって、x'³ = ξ'³(b(t), t) の場合には、
|∂(x¹, x², x³)/∂(x'¹, x'², x'³)|δ³(x - ξ(σ, t)) = δ(x'¹ - ξ'¹(b(t), t))δ(x'² - ξ'²(b(t), t))δ(σ - b(t))/|∂₁ξ'³(b(t), t)|.
この事を使うと、
∫dS・j(x, t) = ∫dx'¹dx'² [∂₁x(x'¹, x'², ξ'³(b(t), t))]×[∂₂x(x'¹, x'², ξ'³(b(t), t))]・∫_-∞^∞ dσ|∂₁ξ(σ, t)|ρ'(σ, t)u'(σ, t)δ(x'¹ - ξ'¹(b(t), t))δ(x'² - ξ'²(b(t), t))δ(σ - b(t))/[|∂₁ξ'³(b(t), t)||∂(x¹, x², x³)/∂(x'¹, x'², x'³)|_{x'3 = ξ'3(b(t), t)}]
= ∫dx'¹dx'² [∂₁x(x'¹, x'², ξ'³(b(t), t))]×[∂₂x(x'¹, x'², ξ'³(b(t), t))]・|∂₁ξ(b(t), t)|ρ'(b(t), t)u'(b(t), t)δ(x'¹ - ξ'¹(b(t), t))δ(x'² - ξ'²(b(t), t))/[|∂₁ξ'³(b(t), t)||∂(x¹, x², x³)/∂(x'¹, x'², x'³)|_{x'3 = ξ'3(b(t), t)}]
= [∂₁x(ξ'¹(b(t), t), ξ'²(b(t), t), ξ'³(b(t), t))]×[∂₂x(ξ'¹(b(t), t), ξ'²(b(t), t), ξ'³(b(t), t))]・|∂₁ξ(b(t), t)|ρ'(b(t), t)u'(b(t), t)/[|∂₁ξ'³(b(t), t)||∂(x¹, x², x³)/∂(x'¹, x'², x'³)|_{x' = ξ'(b(t), t)}].
ところが、
[∂₁x(ξ'(b(t), t))]×[∂₂x(ξ'(b(t), t))] = |∂₁x(ξ'(b(t), t))||∂₂x(ξ'(b(t), t))|n₂(t)
だし、
|∂(x¹, x², x³)/∂(x'¹, x'², x'³)|_{x' = ξ'(b(t), t)} = [∂₁x(ξ'(b(t), t))]×[∂₂x(ξ'(b(t), t))]・[∂₃x(ξ'(b(t), t))]
　= |∂₁x(ξ'(b(t), t))||∂₂x(ξ'(b(t), t))||∂₃x(ξ'(b(t), t))|
だから、
∫dS・j(x, t) = n₂(t)・|∂₁ξ(b(t), t)|ρ'(b(t), t)u'(b(t), t)/[|∂₁ξ'³(b(t), t)||∂₃x(ξ'(b(t), t))|].
ここで、
∂₁ξ'³(b(t), t) = [∂₁ξ(b(t), t)]・∇x'³(ξ(b(t)), t) = [∂₁ξ(b(t), t)]・n₂(t)|∇x'³(ξ(b(t), t)|,
|∇x'³(ξ(b(t), t)||∂₃x(ξ'(b(t), t))| = 1
∵ [∂₃x(ξ'(b(t), t))]・∇x'³(ξ(b(t), t) = ∂x'³/∂x'³ = 1, ∂₃x(ξ'(b(t), t)) と ∇x'³(ξ(b(t), t) は平行。
である事を使うと、
∫dS・j(x, t) = |∂₁ξ(b(t), t)|n₂(t)・u'(b(t), t)ρ'(b(t), t)/|n₂(t)・∂₁ξ(b(t), t)|.
同様にして、x = ξ(a(t), t) での電流を求めるのに適した曲線座標系 x''¹-x''²-x''³系を導入し、Sのうちで x = ξ(b(t), t) を含む領域については面積分でx'¹-x'²-x'³系を使い、x = ξ(a(t), t)を含む領域については面積分でx''¹-x''²-x''³系を使う、という風にすれば、
∫dS・j(x, t) = |∂₁ξ(b(t), t)|n₂(t)・u'(b(t), t)ρ'(b(t), t)/|n₂(t)・∂₁ξ(b(t), t)| + |∂₁ξ(a(t), t)|n₁(t)・u'(a(t), t)ρ'(a(t), t)/|n₁(t)・∂₁ξ(a(t), t)|.
そもそも、∫dS・j(x, t)の値は線状連続体とSの交点でのρ'の値、u'の値、n'の値、Sの単位法線ベクトル、の4つだけで決まる事が直感的に明らかなので、Sが平面である場合の結果とSが曲面である場合の結果が一致する事は、やってみなくても分かる事です。
ここまで補足説明を書いてみると、CAN-2-1-5の前半部分に「⑤ 線状電荷」という項目が有っても良いと感じます。
しかし、それなら面状電荷については何故書かないのか、という批判は妥当です。2021.08.27,28,31;2021.09.01,02,04,05,06;2021.11.29

12行目の「(6) 荷電粒子(電荷q)」は、13～20行目の記事のタイトルです。2021.08.20

13,14行目の式と u(z(t), t) = (d/dt)z(t) である事から、
ρ(x, t)u(x, t) = qδ³(x - z(t))u(x, t)
　= qδ³(x - z(t))u(z(t), t)　∵ (d6)
　= qδ³(x - z(t))(d/dt)z(t)
　= j(x, t).
これはCAN-2-1-4-27の式に一致します。
(d6)を適用する部分を詳しく書くと、次の様に成ります。
δ³(x - z(t))u(x, t) = δ(x¹ - z¹(t))δ(x² - z²(t))δ(x³ - z³(t))[iu¹(x¹, x², x³, t) + ju²(x¹, x², x³, t) + ku³(x¹, x², x³, t)],
δ(x¹ - z¹(t))δ(x² - z²(t))δ(x³ - z³(t))u^k(x¹, x², x³, t) = δ(x¹ - z¹(t))δ(x² - z²(t))δ(x³ - z³(t))u^k(z¹(t), z²(t), z³(t), t)
∴ δ³(x - z(t))u(x, t) = δ(x¹ - z¹(t))δ(x² - z²(t))δ(x³ - z³(t))[iu¹(z¹(t), z²(t), z³(t), t) + ju²(z¹(t), z²(t), z³(t), t) + ku³(z¹(t), z²(t), z³(t), t)]
　　　= δ³(x - z(t))u(z(t), t).
//2021.10.03,04

16,17行目の式の根拠は以下です。
(∂/∂t)f(x - z(t)) = Σ_k=1³ [(∂/∂t)(x^k - z^k(t))]∂_kf(x - z(t)) = Σ_k=1³ [-(d/dt)z^k(t)]∂_kf(x - z(t)) = -[(d/dt)z(t)]・∇f(x - z(t)).
//2021.10.04

18,19行目の式の根拠は以下です。
∇・j(x, t) = Σ_k=1³ ∂_kj^k(x, t) = Σ_k=1³ (∂/∂x^k){q[(d/dt)z^k(t)]δ³(x - z(t))} = Σ_k=1³ q[(d/dt)z^k(t)]∂_kδ³(x - z(t)) = q[(d/dt)z(t)]・∇δ³(x - z(t)).
//2021.10.04

2006年08月22日にセルジ・レニーヌさんから教えてもらった事を受けて記入した補足説明は以下です。
その後、ここまでの補足説明を追記したので、今では以下の補足説明を読まなくても読み進める事が出来る様に成っています。2021.12.03

CAN-2-1-5-2，3 の ρ’ は、電荷の分布する線上の点以外の点では値が 0 と成る関数です。

この事は、電荷の分布する線以外の至るところを、電荷の線密度がゼロの電荷分布線が通っている、と考える事によって、理解する事も出来ます。

CAN-2-1-5-3 の表式において、 δ ( 0 ) が現れるのを避けるには、次のように書けば良い。

ρ ( x ， y ， z ，t )
＝ ∫ ｄｓ ρ’ ( x ， y ， z ； t ) δ ( x － x’ ( s ； t ) ) δ ( y － y’ ( s ； t ) ) δ ( z － z’ ( s ； t ) )

ただし、 ( x’ ( s ； t ) ， y’ ( s ； t ) ， z’ ( s ； t ) ) は、時刻 t における、電荷の分布する線上の点の座標のパラメータ表示 ( s がパラメータ ) で、パラメータ s は、
[ ∂ x’ ( s ； t ) ／ ∂ s ]² ＋ [ ∂ y’ ( s ； t ) ／ ∂ s ]² ＋ [ ∂ z’ ( s ； t ) ／ ∂ s ]² ＝ 1
という条件を満たすように選ばれているものとする。

δ ( 0 ) 記号について。

[ δ ( 0 ) ]^{ｎ－ｋ} は、実 n 変数関数を実 n 変数関数に写す写像であり、 n 次元空間の k 次元部分集合に（電荷や質量の）密度分布が集中している場合、 f を、その部分集合内の点においては k 次元的密度を値として持ち、それ以外の点においてはゼロを値として持つ、任意の関数とするとき、この密度分布を n 次元的密度に換算して、問題となっている n 次元空間の密度分布を表す n 変数関数を F とするならば、 [ δ ( 0 ) ]^{ｎ－ｋ} は、 f を F に写す。

すなわち、[ δ ( 0 ) ]^{ｎ－ｋ} f ＝ F
これを [ δ ( 0 ) ]^{ｎ－ｋ} の定義とする。

当然、 1 つの n － k に対して複数の ( n ， k ) の組み合わせが存在する。

CAN-2-1-5-2，3 は n ＝ 3 ， k ＝ 1 の場合だ。

精密に書くと、
[ δ ( 0 ) ]² ρ’ ( □ ， □ ， □ ， t ) ＝ ρ ( □ ， □ ， □ ， t )

これを、 n ＝ 4 ， k ＝ 2 の場合と見なして、[ δ ( 0 ) ]² ρ’ ＝ ρ としても良いのかどうかは、宇田は未確認。

分かった人は御一報ください。

気を付けなくてはいけないのは、 δ ( 0 ) を 1 つの数の如く見なして、
[ δ ( 0 ) ]² f ( x ， y ， z ) ＝ [ δ ( 0 ) ]² [ f ( x ， y ， z ) ]
という風にしてはいけない、という点だ。

[ δ ( 0 ) ]² f ( x ， y ， z ) ＝ [ [ δ ( 0 ) ]² f ] ( x ， y ， z )
であって、
[ [ δ ( 0 ) ]² f ] ( x ， y ， z ) ＝ [ δ ( 0 ) ]² [ f ( x ， y ， z ) ]
という式変形は出来ない。

この事態を、結合則が成り立たない、と表現しても良かろう。

なお、 δ ( 0 ) 記号は、宇田の発明であって一般に認められたものではないので、学校への宿題の提出においては使わない方が無難だ。

▲このページの上端へ行く

【SEOテキスト】04.4.4,宇田雄一,第2章,電荷と電流,⑤線状電流,電荷の線密度をρ'(x,t)とすると、,ρ(x,t)=[δ(0)]2ρ'(x,t),j(x,t)=ρ(x,t)u(x,t),uは速度場,線に沿って測った長さをsとする時、電荷の保存則は,0=,∂ρ'(x(s),t),-,∂t,+,∂,-,∂s,[ρ'(x(s),t)n(s)・u(x(s),t)],ただし、n(s)≡dx(s)/ds,∴,dρ',-,dt,+ρ',∂v,-,∂s,=0 (,dρ',-,dt,≡,∂ρ',-,∂t,+v,∂ρ',-,∂s,),ただし、v≡n(s)・u(x(s),t),⑥荷電粒子(電荷q),ρ(x,t)=qδ3(x-z(t)),j(x,t)=q,(t)δ3(x-z(t)),ただしz(t)は時刻tにおける粒子の位置を表す。,∂ρ,-,∂t,=-q,(t)・∇δ3(x-z(t)),∇・j=q,(t)・∇δ3(x-z(t)),故に電荷の保存則が成り立つ。