
次のページ
前のページ
目次
CAN-2-1-2
CAN-2-1-4
CAN-2-1-7
[補足説明欄]
ガウスの定理は以下の論法を一般化する事によって証明されます。
V = { (x, y, z) | a ≦ z ≦ b and f(z) ≦ y ≦ g(z) and p(y, z) ≦ x ≦ q(y, z)} とし、
Vの境界がSで、内側を裏、外側を表とする場合には、
∫V d3x ∂1J1(x) = ∫ab dz ∫f(z)g(z) dy ∫p(y, z)q(y, z) dx ∂J1(x, y, z)/∂x
= ∫ab dz ∫f(z)g(z) dy [J1(q(y, z), y, z) - J1(p(y, z), y, z)]
= ∫dS・i J1(x) ∵ x = q(y, z) ⇒ dydz = dS・i and x = p(y, z) ⇒ dydz = -dS・i.
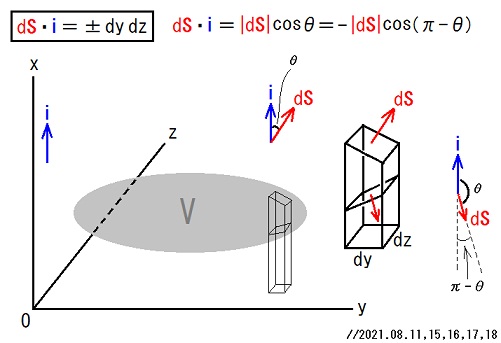
ここでさらに、
V = { (x, y, z) | a' ≦ y ≦ b' and f'(y) ≦ x ≦ g'(y) and p'(y, x) ≦ z ≦ q'(y, x)} とも書けるし
V = { (x, y, z) | a'' ≦ x ≦ b'' and f''(x) ≦ z ≦ g''(x) and p''(x, z) ≦ y ≦ q'(x, z)} とも書ける場合を考える。
この場合には
∫V d3x ∂2J2(x) = ∫dS・j J2(x),
∫V d3x ∂3J3(x) = ∫dS・k J3(x)
だから、
∫V d3x [∂1J1(x) + ∂2J2(x) + ∂3J3(x)] = ∫dS・[J1(x)i + J2(x)j + J3(x)k]
これは、
∫V d3x ∇・J(x) = ∫dS・J(x)
である事を意味します。2021.08.10,11,15,16,17,18
7,8行目でCAN-2-1-2-24,25を誤まってCAN-2-1-2-24-25と書いてしまっています。
【SEOテキスト】宇田雄一CAN-2-1-4-20,21ガウスの定理を用いた。CAN-2-1-7-29,30,14,CAN-2-1-2-24,25が成り立てばCAN-2-1-7-14は自動的に成り立つ。この事を自分で確かめておくこと。逆にCAN-2-1-7-14が成り立つならば∃A;CAN-2-1-2-24-25が成り立つ。これは証明しなくても良い。[ゲージ変換]A'μ(x)=Aμ(x)+∂μλ(x)で∂ν∂μA'ν=0と出来るか?∂νA'ν=0と出来れば十分。∂νAν+∂ν∂νλ=0を満たすλは常に存在する。故に出来る。