
次のページ
前のページ
目次
TEC-0-2-3
COM-2-1
[補足説明欄]
1行目の上の「第2章 電荷と電流」は、CAN-2-1-4からCAN-2-1-6までの記事のタイトルです。
この部分で説明されているのが、日常語の「電気」という言葉に該当する概念です。
この他に「電圧」という概念が日常語の「電気」という言葉で表される場合が有りますが、当典では電圧の話はしません。
電圧は理学ではなく工学に分類されるべき概念だからです。
自宅のコンセントに「電気が来てる」と言えば、それは、端子間に百ボルトの電圧が掛かっている、という意味です。
電気製品を接続して稼働させなければ電流はゼロですが、それでも電圧が有れば「電気が来てる」という言い方で間違っていません。
水道の栓を開かなければ水流はゼロですが、もし栓を開けば水が出る様に水圧が掛かっていれば「水が来てる」と言えるのと同様です。
電流を水流に例えた時に水圧に例えられる何か、が電圧です。
しかし狭義で言うなら、電荷、電流、電圧のうちの電荷(でんか)が電気の正式名称です。2021.07.18,19,20;2021.10.08,18
1行目の「 [1] 3次元記法で」は、CAN-2-1-4-2からCAN-2-1-5-20までの記事のタイトルです。2021.07.18
2行目の「 (1) 電荷密度と電流密度」は、3~6行目の記事のタイトルです。
この部分では、CAN-2-1-1-1~12に書式を出来るだけ揃えました。
CAN-2-1-1-1~12は電磁場について、CAN-2-1-4-2~6は電気についてです。2021.07.18,20,21
電荷密度という概念を理解するには、質量密度という概念を参考にするのが有効です。
質量密度を (質量)÷(体積) の事だと理解している人が居るかもしれませんが、質量密度は本当は考える部分の体積をゼロに近付けた時の (その部分の質量)÷(その部分の体積) の極限値として各点ごとに定義されます。
質量密度がどの点でも同じならば (質量密度) = (全体の質量)÷(全体の体積) ですが、質量密度が点ごとに違うなら、そうは言えません。
また「質量密度がどの点でも同じならば (質量密度) = (全体の質量)÷(全体の体積) である」事は、自明ではありません。
自明ではないというのは、数学(論理)ではなく物理(質量の性質)だという事です。
電荷(電気)を帯びた物体でも、全体としてどれだけの電荷を帯びているかだけでなく、任意の部分がどれだけの電荷を帯びているかも問題です。
そこで、質量密度を考えたのと同様の理由で、電荷密度というものを考えるわけです。
電荷密度は考える部分の体積をゼロに近付けた時の (その部分の電荷)÷(その部分の体積) の極限値として各点ごとに定義されます。
電荷密度がどの点でも同じならば (電荷密度) = (全体の電荷)÷(全体の体積) ですが、全体の質量と違って全体の電荷が問われる事は、あまり有りません。
また「電荷密度がどの点でも同じならば (電荷密度) = (全体の電荷)÷(全体の体積) である」事も、自明ではありません。
電荷の方が電荷密度より基礎的であるとは言えないので、この補足説明で電荷を使って電荷密度を定義した事は説明上の便法だと考えて下さい。
その意味で、COM-2-6-1~16で説明されている様に電磁場を定義され得ない基礎概念だとしておくと同時に、電荷密度と電流密度も基礎的な物理量だから定義されないとしておく、というのが当典の紙部分のスタイルに成っています。2021.07.19,20;2021.10.08,09
3行目の「ρ: R4 → R」は「R4からRへの写像であるρ」という意味です。
従がって、x ∈ R3, t ∈ R とする時、ρ(x, t) ∈ R です。
質量密度と違って ρ(x, t) < 0 は可能です。2021.07.20,21;2021.10.09,18
3行目の「j: R4 → R3」は「R4からR3への写像であるj」という意味です。
従がって、x ∈ R3, t ∈ R とする時、j(x, t) ∈ R3 つまり k = 1, 2, 3 に対して jk(x, t) ∈ R です。2021.07.20,21;2021.10.09
7行目の「 (2) 電荷と電流」は、8~15行目の記事のタイトルです。2021.07.18
9,10行目の積分は体(積)積分です。
面積分が面積積分と呼ばれるのを見た事は有りませんが、体積分は体積積分とも呼ばれる様です。
英語では「体積分」は「volume integral」で、「volume」に「立体」という意味は無いので、「volume integral」の直訳は「体積積分」だと思われます。
例えば V = { (x, y, z) | a ≦ z ≦ b and f(z) ≦ y ≦ g(z) and p(y, z) ≦ x ≦ q(y, z)} の場合には、
∫V d3x ρ(x, t) = ∫ab dz ∫f(z)g(z) dy ∫p(y, z)q(y, z) dx ρ(x, y, z, t) ・・・ (1)
という風に計算します。
a = Vの点の中でz座標が最小の点のz座標、
b = Vの点の中でz座標が最大の点のz座標、
f(z) = z軸に垂直な平面でVを切った断面の点の中でy座標が最小の点のy座標、
g(z) = z軸に垂直な平面でVを切った断面の点の中でy座標が最大の点のy座標、
p(y, z) = z座標とy座標を指定して得られる直線とVの交わりの中でx座標が最小の点のx座標、
q(y, z) = z座標とy座標を指定して得られる直線とVの交わりの中でx座標が最大の点のx座標。
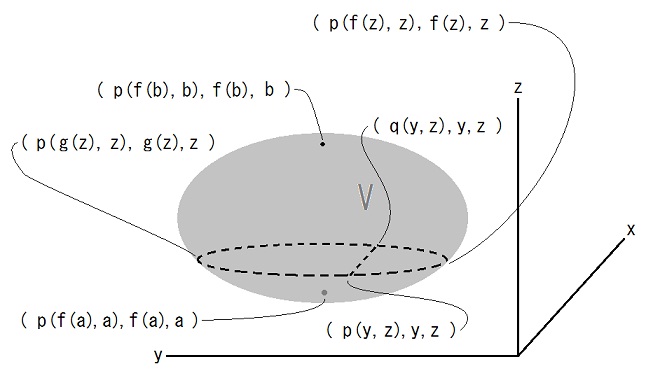
この図では p(f(z), z) = q(f(z), z), p(g(z), z) = q(g(z), z), f(a) = g(a), f(b) = g(b) です。
VをN個の領域に分割した時のk番目の領域の体積をvN(k), k番目の領域内の代表点をxN(k)とする時、
∫V d3x ρ(x, t) = limN→∞Σk=1N vN(k)ρ(xN(k), t) ・・・ (2)
これが体(積)積分の定義です。
ただし、Vの分割は、等分と大きく違い過ぎない様に、また各領域のx幅とy幅とz幅が同程度である様に、行うものとします。
(1)と(2)が等価である事(下の青枠)は、物理ではなく数学ですが自明ではなく、微積分学の基本定理(下の赤枠)に分類されるでしょう。2021.08.03,04,05,06,07;2021.10.10,11,12,13,15,19,22
| f, F: R → R and f = DF and a < b とし、{x| a ≦ x < b}をN個に分割したk番目の要素を{x| aN(k) ≦ x < bN(k)}とし、aN(k) < xN(k) < bN(k) とします。 ただし、aN(1) = a and bN(N) = b and bN(k) = aN(k + 1) and bN(k) - aN(k) = (b - a)/N だとします。 DはTEC-0-1-43の補足説明欄の赤枠内で説明されている写像です。 この時、limN→∞Σk=1N [bN(k) - aN(k)]f(xN(k)) = F(b) - F(a) ・・・ (r1). これを微積分学の基本定理と呼びます。 (r1)の左辺は定積分∫ab dx f(x) だから、定積分と不定積分の関係を言っているのが微積分学の基本定理だ、と言えます。 微積分学の基本定理の証明の骨子は limN→∞Σk=1N [bN(k) - aN(k)]DF(xN(k)) = F(b) - F(a) ・・・ (r2) です。 (r2)が成り立つ事は、下図を見れば分かります。 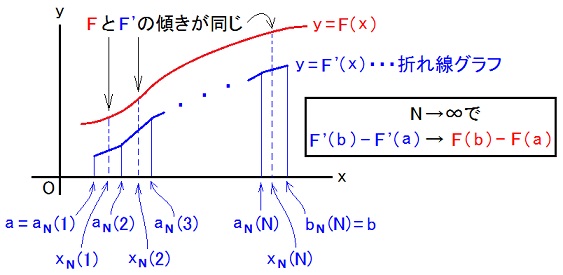 物理学ではそれ以上詮索する必要は有りませんが、数学では個々の [bN(k) - aN(k)]DF(xN(k)) - [F(bN(k)) - F(aN(k))] が N → ∞ でゼロに近付くからと言ってそれらの和までゼロに近付くとは限らないじゃないか項数を無限に増やすんだから、という点を追求し、それでもゼロに近付くんだという事を証明します。 微積分学の基本定理は、曲線 y = f(x) とx軸と直線 x = a と直線 x = b で囲まれた図形の面積が F(b) - F(a) に成る事だと解釈できます。 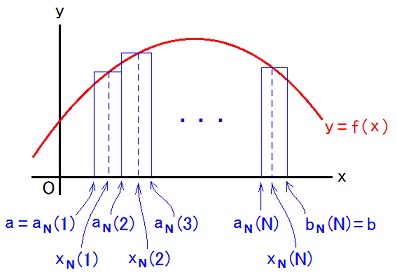 この図で、矩形の面積の和が N → ∞ で、曲線 y = f(x) とx軸と直線 x = a と直線 x = b で囲まれた図形の面積に近付く事が、(r1)の左辺の図解です。 私が高校生だった1980年代にはグラフの面積を積分で求める問題が高校数学で出題されていましたが、定積分の計算が不定積分に帰着するのが何故なのかは全く言及されませんでした。 そのため、ほとんどの生徒は、定積分の問題が無断で不定積分の問題にすり替えられている事に気付いていない様子でした。 高校生の頃の私は、その事を見抜いて得意に成っていました。 ただし、私が高校生だった1980年代には高校数学では、∫ab f(x) dx = F(b) - F(a) が定積分の定義だと教えられていました。 だから正確には、つながってなかったのは、定積分と不定積分ではなく、定積分とグラフの面積でした。 高校の数学教育の伝統のこの轍は、矯正されるべきかもしれませんが、しかし、矯正せずにそのままにしておいて、大学の数学で初めて微積分学の基本定理を習った時に、その事に今まで自分が気付かなかった事にシッカリ驚いてもらう方が教育的かもしれません。 自明ではない事、証明を要する事に気付くのも数学の大切な能力です。 大学1年生の時の私は ΣjΣk ajk = ΣkΣj ajk である事すら自明とせず立ち止まって考えたものです。 //2021.10.11,12,13,15,16,20,22 |
| 例えば V = {(x, y, z)| a < x < a' and b < y < b' and c < z < c'} である場合、 vN(k) = vN(p, q, r) = vN ≡ [(a' - a)/N][(b' - b)/N][(c' - c)/N], xN(k) = xN(p, q, r) = [a + (p - 1/2)(a' - a)/N]i + [b + (q - 1/2)(b' - b)/N]j + [c + (r - 1/2)(c' - c)/N]k として、 ∫V d3x ρ(x) = limN→∞Σp=1NΣq=1NΣr=1N vN(p, q, r)ρ(xN(p, q, r)) = limN→∞Σp=1NΣq=1NΣr=1N [(a' - a)/N][(b' - b)/N][(c' - c)/N] ×ρ(a + (p - 1/2)(a' - a)/N, b + (q - 1/2)(b' - b)/N, c + (r - 1/2)(c' - c)/N) = limN→∞ limN'→∞ limN''→∞Σp=1NΣq=1N'Σr=1N'' [(a' - a)/N][(b' - b)/N'][(c' - c)/N''] ×ρ(a + (p - 1/2)(a' - a)/N, b + (q - 1/2)(b' - b)/N', c + (r - 1/2)(c' - c)/N'') ・・・※ = limN→∞ limN'→∞ Σp=1NΣq=1N' [(a' - a)/N][(b' - b)/N'] limN''→∞Σr=1N'' [(c' - c)/N''] ×ρ(a + (p - 1/2)(a' - a)/N, b + (q - 1/2)(b' - b)/N', c + (r - 1/2)(c' - c)/N'') = limN→∞ limN'→∞ Σp=1NΣq=1N' [(a' - a)/N][(b' - b)/N']∫cc' dz ρ(a + (p - 1/2)(a' - a)/N, b + (q - 1/2)(b' - b)/N', z) = limN→∞ Σp=1N [(a' - a)/N] limN'→∞ Σq=1N' [(b' - b)/N']∫cc' dz ρ(a + (p - 1/2)(a' - a)/N, b + (q - 1/2)(b' - b)/N', z) = limN→∞ Σp=1N [(a' - a)/N]∫bb' dy∫cc' dz ρ(a + (p - 1/2)(a' - a)/N, y, z) = ∫aa' dx∫bb' dy∫cc' dz ρ(x, y, z) と出来ます。 この考え方を私は日本物理学会2008年秋季大会の物理教育についての20aRAセッションで発表しました。 その報告記事が日本物理学会2008年秋季大会@学会発表@活動報告@学問@宇田英才教室に書かれています。 勝木渥先生が、微積分学の基本定理を自明だと誤解していたのか、私の発表内容を「当たり前の事だから説明の必要は無い」と言って、既存の教科書をかばう発言をした事が、そこに書かれています。 物理学の学生にとって、微積分学の基本定理は数学で1次元の場合を習うだけで、物理学の教科書では体(積)積分が説明なしで用いられます。 これを私は伝統の轍(わだち)の舌足らずな部分だと考えています。 伝統の轍の矯正は、まず間違っていると、間違っていなければ新しくないと、間違ってもいないし新しければ当たり前の事だから書く必要が無いと、この様なたちの悪い批判を受ける傾向が非常に強い。 しかし、もしその様な批判が通って伝統の轍が矯正されないまま存続したならば、それは学習者にとって不便です。 批判する人は、伝統の轍を学習者が不便だと感じるものだ、伝統の轍の私による矯正を学習者が便利だと感じるものだ、という事の証拠を私が提示できないのを良い事に、学習者はそういう風には感じないのが普通だと吹っかけます。 勝木渥先生の他に並木雅俊先生も、日本物理学会2009年秋季大会の28aVEセッションで、解析力学では関数と関数の値を区別しなければいけないという私の発表(TEC-0-1-43補足説明欄赤枠内で注意が喚起されている事項)で勝木渥先生と似た様な事を言いました。 その事が日本物理学会2009年秋季大会@学会発表@活動報告@学問@宇田英才教室の後半に書かれています。 その様な態度が、先生の自分の相対的評価を下げられない事を生徒の利益よりも不当に優先する態度であるかどうかは、読者各位が伝統の轍の私による矯正を便利や必要だと感じるかどうかによって今後検証されて行く事でしょう。 ※ 極限操作を3つに分けて3つの極限操作を独立に行なってもよい事は、次の様に考えれば分かります。 簡単の為に limN→∞ f(N, N) = limN→∞ limN'→∞ f(N, N') なのかという問題(極限操作を2つに分ける場合)を考えてみます。 limN'→∞ f(N, N') = αN ・・・ (b1) とすると、 ∀ε > 0; ∃δN(ε); N' > δN(ε) ⇒ |f(N, N') - αN| < ε ・・・ (b2). ここで N > N0(ε) ⇒ δN(ε) < N ・・・ (b3) だと仮定します。 例えば δN(ε) が N → ∞ で収束するならば、この様なN0が必ず存在します。 limN→∞ αN = β ・・・ (b4) とすると、 ∀ε > 0; ∃δ'(ε); N > δ'(ε) ⇒ |αN - β| < ε ・・・ (b5). この場合、 N > N0(ε/2) ⇒ N > δN(ε/2) ∵ (b3) ⇒ |f(N, N) - αN| < ε/2 ∵ (b2), N > δ'(ε/2) ⇒ |αN - β| < ε/2 ∵ (b5) だから、 ∀ε > 0; N > max{N0(ε/2), δ'(ε/2)} ⇒ |f(N, N) - β| ≦ |f(N, N) - αN| + |αN - β| < ε/2 + ε/2 = ε ∴ limN→∞ f(N, N) = β = limN→∞ αN = limN→∞ limN'→∞ f(N, N'). ただし max{N0(ε/2), δ'(ε/2)} はN0(ε/2)とδ'(ε/2)のうちの大きい(小さくない)方です。 //2021.10.12,15,16,23,24,25;2021.11.27,28 |
電荷とは何かが先に分かっていたならば、8~10行目の内容が任意のVに対して成り立つ事が電荷密度の定義に成った所です。
しかし実際には電荷で電荷密度を定義するのではなく電荷密度で電荷を定義するスタイルで紙部分を私は書いています。2021.07.19;2021.10.25
13,14行目の積分は面積分です。
紙部分(18,19行目も)では積分範囲Sを明記するのを忘れています(※)。
正: ∫S dS・j(x, t)
誤: ∫dS・j(x, t)
SをN個の領域に分割した時のk番目の領域の面積をsN(k), k番目の領域内の代表点をxN(k), 代表点での単位法線ベクトルをnN(k)とする時、
∫S dS・j(x, t) = limN→∞Σk=1N sN(k)nN(k)・j(xN(k), t) ・・・ (3)
これが面積分の定義です。
ただし、Sの分割は、等分と大きく違い過ぎない様に、また各領域の縦幅と横幅は同程度である様に、行うものとします。
単位法線ベクトルは、Sの裏から表に向かいSに垂直な単位ベクトルです。
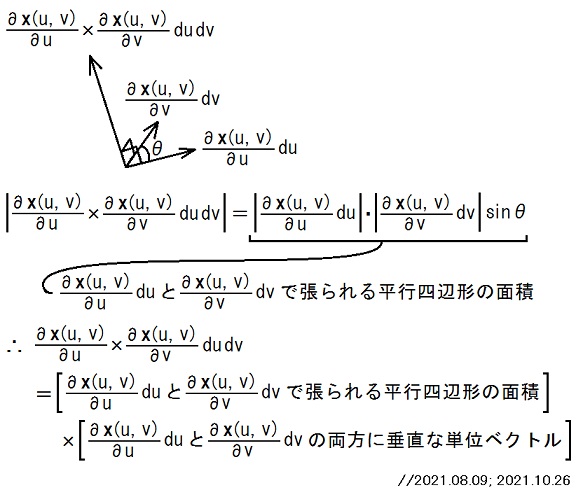
Sのパラメータ表示を x = x(u, v), a ≦ v ≦b, f(v) ≦ u ≦ g(v) とすると、
[(∂/∂u)x(u, v)]×[(∂/∂v)x(u, v)] の向きがSの裏から表に向かう向きならば
∫S dS・j(x, t) = ∫ab dv ∫f(v)g(v) du [(∂/∂u)x(u, v)]×[(∂/∂v)x(u, v)]・j(x(u, v), t),
[(∂/∂v)x(u, v)]×[(∂/∂u)x(u, v)] の向きがSの裏から表に向かう向きならば
∫S dS・j(x, t) = ∫ab dv ∫f(v)g(v) du [(∂/∂v)x(u, v)]×[(∂/∂u)x(u, v)]・j(x(u, v), t)
という風に計算します。
※ 面積分を表す記号としては ∫S dS・j(x, t) というタイプの記号が使われるのが慣習ですが、この記号にはどの変数で積分するかが書かれていない点を私は不満に思います。
しかし例えば、∫S d2x・j(x, t) と書いたのでは、d2x が dS を表しているとする事が、被積分関数がベクトル値関数ではなく実数値関数である場合の2重積分で使われる d2x という記号の意味と食い違い、同じ記号を複数の意味で用いるのも出来るだけ避けたい所です。
そこで、あえて詳しく書きたい場合には次の様に書いたらどうでしょうか。
例: ∫x∈S dS・j(x, t), ∫x∈A dA・j(x, t), etc.
これは私からの提案です。2021.08.07,09;2021.10.25,26,27;2021.11.02,03,05,27
電流とは何かが先に分かっていたならば、11~15行目の内容が任意のSに対して成り立つ事が電流密度の定義に成った所です。
しかし実際には電流で電流密度を定義するのではなく電流密度で電流を定義するスタイルで紙部分を私が書いている事が、15行目の言い回しから分かります。
電磁気学で電流密度を考えるのは、一般の場合を考える、詳細まで余す所なく記述する、という物理学の特徴を良く表しています。
電流は電線を流れているとは限らない、立体的な広がりを持って大地や海中を流れている電流だって有るだろうし、電線を流れている電流も細かく見れば断面内の場所ごとに電流密度が違うわけです。
それに対して、工学で電流密度なんて概念を使う分野は非常に少ない事でしょう。
こういう所にも、工学と理学の性格の違いが出ています。
理学は、それで全部なのか、まだ有るなら全部書け、という態度なのに対して、工学は、活用しない情報はオミットしろ、という態度です。2021.07.19,20,21;2021.10.27
16行目の「 (3) 電荷の保存則」は、17~25行目の記事のタイトルです。2021.07.18
18,19行目の式は、
(V内の電荷の増加速度) = -(Vから流出する電流)
という意味です。
意訳すれば、電流とは電荷の単位時間当たりの移動の事である、という意味です。
もし全空間の電荷の合計が有限ならば、
(V内の電荷の増加速度) = -(Vから流出する電流)
(V外の電荷の増加速度) = -(Vに流入する電流)
∴ (V内の電荷の増加速度) + (V外の電荷の増加速度) = -(Vから流出する電流) - (Vに流入する電流) = 0
∵ -(Vから流出する電流) = (Vに流入する電流).
これは (V内の電荷) + (V外の電荷) が変化しないという事だから高校物理の「電荷の保存則」に一致します。
高校物理と違って大学の物理学では、保存則を表す式としては18,19行目の式を変形して得られる23,24行目の式の形の式を基本とします。
この事を私は日本物理学会2007年春季大会の物理教育についての19pXJセッションで「大学物理での保存則」というタイトルで発表しました。
18,19行目の式なら、全空間の電荷の合計が有限でなくても意味が分かります。
これに対して、全空間の電荷の合計は時間が経っても変化しない、と言ったのでは、全空間の電荷の合計が有限でない場合には、何の事か分かりません。
この事を私は「良く定義されていない(well-definedではない)」と言うのだと誤解していましたが、インターネットで調べてみて自分の間違いに気付きました。
「well-definedではない」という表現は主に、絞り込む条件が足りなくて答えが1つに定まらない、という意味で使われるようです。
これに対して、3 ÷ x が x = 0 で定義されていない事を「良く定義されていない」とは言いませんね。
「良く」は余計なわけです。
そして、「全空間の電荷の合計は時間が経っても変化しない」事が定義されていない場合というのは、こっちです。
18,19行目の式は、物理法則であり、数学の定理ではありません。
電荷の保存則は、「電磁場以外の自由度がどの様であれば電荷密度と電流密度がどう成るか」を決める式(CAN-2-1-4-27;CAN-2-1-5-3,4,13,14)が満たすべき必要条件だ、と考えられます。2021.07.19,20,21,25,27;2021.10.27,30,31;2021.11.01,02,03,27
20,21行目の式の成立根拠は、ガウスの定理です。(TEC-0-2-3-2)2021.07.19
26行目の「 (4) 荷電3次元連続体」は、27~30行目の記事のタイトルです。
3次元連続体には、固体だけでなく流体も含まれます。
「荷電(かでん)」は「電気を荷(に)として負わされている」という意味を表しています。
だから、「荷電3次元連続体」は「電気を荷として負わされている3次元連続体」という意味で、ここでは「静電気を帯びた絶縁体」を考えています。
導体については27行目の式は成り立ちません。
しかし、導体においても電気を運んでいるのは電子であり、電子については27行目の式が成り立つので、27行目の式は一般式だと考えて良いでしょう。
これについて私は、日本物理学会2009年秋季大会の13pSH-4で講演者の金澤喜平さんから面白い意見を聞きました。
金澤喜平さんは、電流なんて流れてないんだ、電子が移動しているだけだ、そして、電流の向きと電子の移動の向きは逆だから電子の移動は電流ではないんだ、と言うんです。
結論を言うと、電流は電荷の移動の数え方だと考えれば電流概念に問題は無い、だから金澤喜平さんは間違っている、というのが答えだと私は思います。
しかし、平均的な学習者は抱(いだ)かずにうっかり通り過ぎてしまうもっともな疑問が金澤喜平さんの意見で呈されているのも事実です。
この人は、自分の意見を私に聞かれるまでは、間違った意見を強情に言い張って他人の助言に耳を貸さない頭が悪い不誠実な人だと思われ続けて来た事でしょう。
しかし真相は、そうではないわけです。
金澤喜平さんの様な先生が持っている誤解や才能を見抜けない物理教育界では、生徒の誤解を解明する事も、生徒の才能を発掘する事も出来ないでしょう。
これについては日本物理学会2009年秋季大会@学会発表@活動報告@学問@宇田英才教室に詳細が書かれています。
電気とは何かを理解するには、この金澤喜平さんの考えを結論の一歩手前で止める感じで理解するのが良いと思います。
電気は物質から離れて電気だけで存在する事が出来ないだけでなく、電気を帯びた物体が電気と物質という2つの部分から(を貼り合わせて)出来ているわけでもないわけです。
電荷は各物体の属性(人に例えるなら身長や視力であって水分とかではない)です。
電流とは物体の移動を電荷のみに着目して数える数え方であって、移動しているのは電荷を持った物体であり、電荷が移動しているわけではない。
放電という言葉が有るじゃないか、と思う人が居るかもしれませんが、放電も電気の物質からの遊離ではありません。
放電という言葉が出来た時には電気が物質から遊離すると考えられていたかもしれませんが、放電でも電流は全て荷電物質の移動に依るというのが真相です。
真空中での放電では例えば電子が陰極から陽極まで飛びます。
放電でも雷では陽極と陰極の間の荷電物質が広範囲に渡ってズレるだけで陰極を出た電子が陽極に達する事は無いでしょう。
電流密度とは何か、電荷密度とは何か、という問題のもっと進んだ答えは、第6章の補足説明欄に書きます。
電子が電気を運ぶ様子はCAN-2-1-5-13,14の式で表されますが、この式はCAN-2-1-4-27の式の十分条件に成っています。
つまり私は、CAN-2-1-4-26~30の(4)荷電3次元連続体を一般論として書き、CAN-2-1-5-1~11の(5)線状電流とCAN-2-1-5-12~20の(6)荷電粒子を具体例として書いています。2021.07.18,20,22,23,28;2021.11.06,07,27
27行目の式と絶縁体の定義が両方成り立つ事は23,24行目の式の十分条件です。
その証明を以下に書きます。
σ = (σ1, σ2, σ3) を3次元連続体の部位を指定するパラメータとし、その部位の時刻tでのデカルト座標を
(x1, x2, x3) = (ξ1(σ1, σ2, σ3, t), ξ2(σ1, σ2, σ3, t), ξ3(σ1, σ2, σ3, t)) つまり x = ξ(σ, t) ・・・ (4)
とすると、
u(ξ(σ, t), t) = u'(σ, t) ≡ (∂/∂t)ξ(σ, t) ・・・ (5).
(4)を逆に解いた結果を
(σ1, σ2, σ3) = (η1(x1, x2, x3, t), η2(x1, x2, x3, t), η3(x1, x2, x3, t)) つまり σ = η(x, t) ・・・ (4a)
としておきます。
また、パラメータσの導入は |∂(ξ1(σ, t), ξ2(σ, t), ξ3(σ, t))/∂(σ1, σ2, σ3)| > 0 と成る様に行うものとします。
ただし、|∂(ξ1(σ, t), ξ2(σ, t), ξ3(σ, t))/∂(σ1, σ2, σ3)| はヤコビアンであり、(j, k)成分が∂ξj(σ, t)/∂σkである行列の行列式です。
CAN-2-1-1-3,4への補足説明の記号法を使うと、(j, k)成分が∂ξj(σ, t)/∂σkである行列は
∂ξ□(σ, t)/∂σ□
と書けるので、
|∂(ξ1(σ, t), ξ2(σ, t), ξ3(σ, t))/∂(σ1, σ2, σ3)| = |∂ξ□(σ, t)/∂σ□| ≡ det[∂ξ□(σ, t)/∂σ□] ・・・ (6).
絶縁体では、tが変化しても変化しないρ'(σ)を使って、
ρ(x, t)|∂(ξ1(σ, t), ξ2(σ, t), ξ3(σ, t))/∂(σ1, σ2, σ3)| = ρ'(σ) ・・・ (7),
ρ(x, t)|∂ξ□(σ, t)/∂σ□| = ρ'(σ) ・・・ (7a).
と書けます。
これが絶縁体の定義です。
(7)(7a)は、感じとしては ρ(x, t)d3x = ρ'(σ)d3σ という意味です。
d3σ内の電荷はρ'(σ)d3σで時間が経っても変化しない、絶縁体が伸縮して同じd3σに対応するd3xが変化するのでその分だけρ(x, t)が変化する、という条件で絶縁体である事を表現しています。
正確には、ξ(σ1, σ2, σ3, t)とξ(σ1 + dσ1, σ2, σ3, t)とξ(σ1, σ2 + dσ2, σ3, t)とξ(σ1, σ2, σ3 + dσ3, t)とξ(σ1 + dσ1, σ2 + dσ2, σ3, t)とξ(σ1 + dσ1, σ2, σ3 + dσ3, t)とξ(σ1, σ2 + dσ2, σ3 + dσ3, t)とξ(σ1 + dσ1, σ2 + dσ2, σ3 + dσ3, t)を頂点とする平行6面体の体積が
[ξ(σ1 + dσ1, σ2, σ3, t) - ξ(σ1, σ2, σ3, t)]×[ξ(σ1, σ2 + dσ2, σ3, t) - ξ(σ1, σ2, σ3, t)]・[ξ(σ1, σ2, σ3 + dσ3, t) - ξ(σ1, σ2, σ3, t)]
= [∂ξ(σ, t)/∂σ1]dσ1×[∂ξ(σ, t)/∂σ2]dσ2・[∂ξ(σ, t)/∂σ3]dσ3
= |∂ξ□(σ, t)/∂σ□|dσ1dσ2dσ3
である事に注意しながら、
ρ(x, t)|∂ξ□(σ, t)/∂σ□|dσ1dσ2dσ3 = ρ'(σ)dσ1dσ2dσ3
から読み取れる内容が(7a)の意味です。
以下では、∂ηj(x, t)/∂xk を ∂σj/∂xk と略記し、∂ξj(σ, t)/∂σk を ∂xj/∂σk と略記します。
また以下では、CAN-1-1-27-18への補足説明に書かれている略記法を使います。
∂σ□/∂x□ = (∂x□/∂σ□)-1 ・・・ (8)
∵ (∂σp/σxq)(∂xq/∂σs) = ∂σp/∂σs = δps.
逆行列の行列式は行列式の逆数だから、(8)より、
|∂σ□/∂x□| = 1/|∂x□/∂σ□| ・・・ (9)
この事と(7a)から、
ρ(x, t) = ρ'(σ)|∂η□(x, t)/∂x□| ・・・ (7b)
さて、
∇・[ρ(x, t)u(x, t)] = ρ(x, t)∇・u(x, t) + u(x, t)・∇ρ(x, t) ・・・ (10)
しかし、
(∂/∂t|σ)f(x, t) ≡ (∂/∂t|σ)f(ξ(σ, t), t) ≡ (∂/∂t)f(ξ(σ, t), t),
(∂/∂t|x)f(ξ(σ, t), t) ≡ (∂/∂t|x)f(x, t) ≡ (∂/∂t)f(x, t)
とすると
∂/∂t|σ = ∂/∂t|x + u(x, t)・∇ ・・・ (11)
∵ (∂/∂t|σ)f(x, t) = (∂/∂t)f(ξ(σ, t), t)
= [(∂/∂t)ξk(σ, t)]∂kf(ξ(σ, t), t) + ∂4f(ξ(σ, t), t)
= [uk(σ, t)]∂kf(x, t) + (∂/∂t)f(x, t) ∵ (4)(5)
だから
∇・[ρ(x, t)u(x, t)] = ρ(x, t)∇・u(x, t) + (∂/∂t|σ)ρ(x, t) - (∂/∂t|x)ρ(x, t)
∴ (∂/∂t|x)ρ(x, t) + ∇・[ρ(x, t)u(x, t)] = ρ(x, t)∇・u(x, t) + (∂/∂t|σ)ρ(x, t)
∴ (∂/∂t)ρ(x, t) + ∇・[ρ(x, t)u(x, t)] = ρ(x, t)∇・u(x, t) + (∂/∂t|σ)ρ(x, t)
この事と(7b)から、
(∂/∂t)ρ(x, t) + ∇・[ρ(x, t)u(x, t)] = ρ'(σ)[|∂σ□/∂x□|∇・u(x, t) + (∂/∂t|σ)|∂σ□/∂x□|] ・・・ (12).
ここで、
|∂σ□/∂x□|∇・u(x, t) + (∂/∂t|σ)|∂σ□/∂x□| = 0 ・・・ (12a)
である事を示せれば、(12)から
(∂/∂t)ρ(x, t) + ∇・[ρ(x, t)u(x, t)] = 0 ・・・ (13)
を証明できた事に成るが、(12a)は絶縁体の伸縮速度とuの自明な関係を表しており、次の様にして証明されます。
まず(9)から、
(∂/∂t|σ)|∂σ□/∂x□| = (∂/∂t|σ)[1/|∂x□/∂σ□|]
= [-1/|∂x□/∂σ□|2](∂/∂t|σ)|∂x□/∂σ□|
= -|∂σ□/∂x□|2(∂/∂t)εpqr[∂ξ1(σ, t)/∂σp][∂ξ2(σ, t)/∂σq][∂ξ3(σ, t)/∂σr]
= -|∂σ□/∂x□|2εpqr{[∂u'1(σ, t)/∂σp][∂ξ2(σ, t)/∂σq][∂ξ3(σ, t)/∂σr]
+ [∂ξ1(σ, t)/∂σp][∂u'2(σ, t)/∂σq][∂ξ3(σ, t)/∂σr]
+ [∂ξ1(σ, t)/∂σp][∂ξ2(σ, t)/∂σq][∂u'3(σ, t)/∂σr]} ∵(5)
= -|∂σ□/∂x□|2[|∂(u'1, x2, x3)/∂(σ1, σ2, σ3)| + |∂(x1, u'2, x3)/∂(σ1, σ2, σ3)| + |∂(x1, x2, u'3)/∂(σ1, σ2, σ3)|] ・・・ (14)
∂kuk(x, t) = (∂σj/∂xk)∂u'k/∂σj = [(∂x□/∂σ□)-1]jk∂u'k/∂σj
= [1/|∂x□/∂σ□|][adj(∂x□/∂σ□)]jk∂u'k/∂σj ・・・ ※
= |∂σ□/∂x□|[|∂(u'1, x2, x3)/∂(σ1, σ2, σ3)| + |∂(x1, u'2, x3)/∂(σ1, σ2, σ3)| + |∂(x1, x2, u'3)/∂(σ1, σ2, σ3)|] ・・・ (15).
ただし εpqr はTEC-0-2-1-11,12で説明されているレビチビタの反対称テンソルです。
(15)の最後の等号の成立根拠は※の末尾に書かれています。
(14)(15)から、(12a)が成立すると分かります。
これで、(13)が証明された事に成り、(13)が成り立つという事は、
j(x, t) = ρ(x, t)u(x, t) ・・・ CAN-2-1-4-27の式
とすればCAN-2-1-4-23,24の式が成り立つという事です。
※ adj(∂x□/∂σ□)は(∂x□/∂σ□)の余因子行列であり、余因子行列の定義はマグロウヒル大学演習シリーズ線形代数(下)207~209に書かれています。
Mを正方行列とするとき、(Mから第j行と第k列を削除して得られる行列の行列式)×(-1)j+k をMの(j, k)成分の余因子と呼び、Mの(j, k)成分の余因子を第(k, j)成分とする行列をMの余因子行列と呼びます。
M-1 = (1/|M|)adj(M) ・・・ (16)
である事は、マグロウヒル大学演習シリーズ線形代数(下)209ページに定理8.8として書かれています。
Mの(j, k)成分をMjkと書けば、
|M| = εpqsM1pM2qM3s
= M11ε1qsM2qM3s + M12ε2qsM2qM3s + M13ε3qsM2qM3s
= M11ε1qsM2qM3s - M12εq2sM2qM3s + M13εqs3M2qM3s
= M11(adj M)11 + M12(adj M)21 + M13(adj M)31
= [M(adj M)]11 ・・・ (17a)
同様にして、
|M| = [M(adj M)]22 = [M(adj M)]33 ・・・ (17b)
また、
[M adj(M)]23 = M21[adj(M)]13 + M22[adj(M)]23 + M23[adj(M)]33
= M21ε1qsM1qM2s - M22εq2sM1qM2s + M23εqs3M1qM2s
= εpqsM2pM1qM2s
= (1/2)(εpqs + εsqp)M2pM1qM2s
= 0 ∵ εsqp = -εpqa.
同様の理由(複数の行が同じなら行列式はゼロに成るという理由)で、j ≠ k ⇒ [M adj(M)]jk = 0 ・・・ (18).
従がって、[M adj(M)]jk = |M|δjk.
∴ (1/|M|)adj(M) = M-1.
この証明を一般化すれば、4次以上の正方行列でも (1/|M|)adj(M) = M-1 が成り立つと分かります。
(17a)(17b)は、vk(adj M)kjがMの第j行をvに置き換えて得られる行列の行列式である事を意味します。
この事が、(15)の最後の等号の成立根拠です。2021.07.19,20;2021.11.08,13,14,15,16,17,20,21,22,23,24,25,26,27,28,29,30;2021.12.01,05
29行目の式は、27行目の式を23,24行目の式に代入する事によって得られます。2021.07.19
30行目では (∂/∂t|σ)ρ(x, t) = (∂/∂t)ρ(ξ(σ, t), t) を dρ/dt と書いています。
30行目の内容は、COM-2-1-7~10でも説明されています。2021.07.19;2021.11.30
【SEOテキスト】宇田雄一,04.4.4,第2章,電荷と電流,[1]3次元記法で,①電荷密度と電流密度,ρ:R4→Rとj:R4→R3を用いて、,時刻t、位置xにおける{,電荷密度はρ(x,t),電流密度はj(x,t),で表される。,②電荷と電流,時刻tに3次元領域V内にある総電荷は、,∫Vd3xρ(x,t),時刻tに裏表を持つ面Sを裏から表に向かって単位時間あたりに通過する電荷は,∫dS・j(x,t),これを電流と呼ぶ。,③電荷の保存則,Vを任意の3次元領域とし、Sをその境界面とすると、,d,-,dt,∫Vd3xρ(x,t)=-∫dS・j(x,t),∴∫Vd3x[,∂ρ(x,t),-,∂t,+∇・j(x,t)]=0,Vは任意だから,∂ρ(x,t),-,∂t,+∇・j(x,t)=0,Sは内側が裏、外側が表、とした。,④荷電3次元連続体,j(x,t)=ρ(x,t)u(x,t),uは速度場,電荷の保存則が成り立つための条件は、,∂ρ/∂t+u・∇ρ+ρ∇・u=0,dρ/dt