
次のページ
前のページ
目次
【補足説明欄】
1,2行目の内容は、CAN-1-1-26-26~30の記事の続きです。2021.01.11;2021.06.08
3行目の「③ Eulerの運動方程式」は、CAN-1-1-27-4からCAN-1-1-28-30までの記事のタイトルです。2021.01.11
Euler は人名です。「オイラー」と読む。
4行目の[慣性テンソル]は、5~25行目の記事のタイトルです。2021.01.11
5行目の「(1) 定義」は、6~10行目の記事のタイトルです。2021.01.11
9,10行目について。
カッコ [ ] 内の右端の項 -rijrik は誤記であり、正しくは -r''ijr''ik です。
正: I''jk = Σi=1n mi[|r''i|2δjk - r''ijr''ik].
誤: I''jk = Σi=1n mi[|r''i|2δjk - rijrik].
miはCAN-1-1-15-10,11で説明されているmiです。
r''i1はPi(CAN-1-1-15-3)の位置のx''1座標、 r''i2はPiの位置のx''2座標、 r''i3はPiの位置のx''3座標です。2021.01.11,13,14
5~10行目について。
(j, k)成分がI''jkである様な行列を慣性テンソルI''だとしています。
本当は、この行列は、慣性テンソルではなく、慣性テンソルの x''1-x''2-x''3系での成分表示だ、とするのが正しい用語法です。
特に、I''11はx''1軸のまわりの慣性モーメント、I''22はx''2軸のまわりの慣性モーメント、I''33はx''3軸のまわりの慣性モーメントとも呼ばれ、それぞれの軸のまわりの回転に対する慣性を表します。
-I''12 = -I''21 と -I''23 = -I''32 と -I''31 = -I''13 は慣性乗積とも呼ばれます。
|r''i|2 = (r''i1)2 + (r''i2)2 + (r''i3)2 だから、
I''11 = Σi=1n mi[(r''i2)2 + (r''i3)2] = Σi=1n mi×(x''1軸とPiの距離)2,
I''22 = Σi=1n mi[(r''i3)2 + (r''i1)2] = Σi=1n mi×(x''2軸とPiの距離)2,
I''33 = Σi=1n mi[(r''i1)2 + (r''i2)2] = Σi=1n mi×(x''3軸とPiの距離)2,
I''12 = I''21 = -Σi=1n mir''i1r''i2,
I''23 = I''32 = -Σi=1n mir''i2r''i3,
I''31 = I''13 = -Σi=1n mir''i3r''i1,
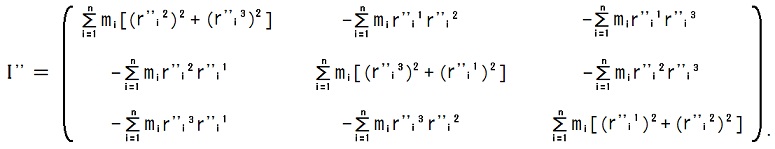
x''1-x''2-x''3系は直交座標系でなくてはいけません。
以下では、 x''1-x''2-x''3系は右手系だとします。2021.01.11,13,14,15,16;2021.06.08
11行目の「(2) 主軸」は、12~25行目の記事のタイトルです。2021.01.11
12,23行目のSO(3)の定義はCAN-1-1-22-19への補足説明に書かれています。2021.06.13
12,13行目について。
Aが時刻に依存しないので、x'' = Ax', A∈SO(3)ならばx'1-x'2-x'3系も剛体に固定された座標系です。
CAN-1-1-22-19への補足説明と同様の理由で、x''1-x''2-x''3系が直交右手系ならばx'1-x'2-x'3系も直交右手系です。
I'は行列だから「I'の成分」という言い方は正しいけれど、行列I'は本当は、慣性テンソルではなく、慣性テンソルのx'1-x'2-x'3系での成分表示です。
だから、CAN-1-1-27-13には本当は「慣性テンソルのx'1-x'2-x'3系による成分表示I'の成分は、」と書く方が正確です。
x'1-x'2-x'3系とx''1-x''2-x''3系の原点が同じならば、x'1-x'2-x'3系による成分表示とx''1-x''2-x''3系による成分表示はどちらも同一の慣性テンソルを表しています。
この事は、3cmと30mmが同一の長さを表しているのと同様です。
長さや慣性テンソルは、それを表す為に使った単位や座標系に左右されません。
そういう量を物理量と呼びます。
左右されない事を物理学では「依存しない」とか「非依存」と言い、座標系に左右されない事を「座標系非依存」と言います。
「座標系非依存」は英語では「frame independent」ですが、これを「座標系独立」とは言いません。
物理量という言葉の意味から分かる様に、「物理」という語は、物理学の専門用語として使われる時には、人工対自然における自然、主観対客観における客観のニュアンスを持っています。
物理量は人間が座標系や単位を発明する前から元々存在しているものです。
それに対して、座標系や単位は人間が作った物です。
物理学における表示と物理量の関係は、文科で言うと言葉と意味の関係です。
日本語の「私は歩いている」と英語の「I am walking」の意味は同じです。
日本語や英語の文法や単語を座標系や単位に、意味を物理量に例える事が出来ます。2021.01.13,14,16,17;2021.06.12,13;2021.07.05
14,15行目の等号は定義です。2021.06.13
16,17行目の等号の成立根拠は r'i = A-1r''i です。
r'i = A-1r''i の成立根拠は、12行目の x'' = Ax' です。2021.01.14
18行目ではΣl=13Σs=13が書かれていませんが、これは略記法です。
Σl=13Σs=13が書かれているものとして読解して下さい。2021.01.14
18行目の等号の成立は、次の様にして示されます。
(A-1)jl[|r''i|2δls - r''ilr''is]Ask
= |r''i|2(A-1)jlδlsAsk - (A-1)jlr''il・Askr''is
= |r''i|2(A-1)jlAlk - (A-1)jlr''il・(A-1)ksr''is ∵ A-1 = At
= |r''i|2(A-1A)jk - (A-1r''i)j・(A-1r''i)k
= |r''i|2δjk - r'ijr'ik ∵ r'i = A-1r''i
= |r'i|2δjk - r'ijr'ik
∵ |r''i|2 = |Ar'i|2 = (Ar'i)・(Ar'i) = (Ar'i)t(Ar'i) = r'itAtAr'i = r'itA-1Ar'i = r'itr'i = r'i・r'i = |r'i|2.
この計算結果にmiを掛けてiについて和を取れば、18行目の等号が成立すると分かります。2021.01.14;2021.02.04,06
20行目の「I'が対称行列になるように」は誤りです。
正しくは「I'が対角行列になるように」です。2021.06.12
22行目の式ではjについての和を取りません。2021.06.12
20~25行目について。
実対称行列はどれも対角化可能である事の証明は、TEC-0-1-46の補足説明欄に書かれています。
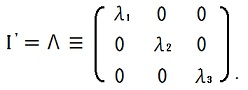
ここでは、x'1-x'2-x'3系の座標軸を主軸だと仮定しても一般性を失わない事が説明されています。
CAN-1-1-13-17,18への補足説明に「一般性を失わない」とはどういう意味かが書かれています。
CAN-1-1-22のx'1-x'2-x'3系の座標軸は主軸だとは限りませんが、後の議論では、これを主軸だと仮定しても一般性を失わない、という事です。2021.01.13,17,23;2021.02.06;2021.06.12
26行目の[角運動量]は、CAN-1-1-27-26からCAN-1-1-28-10までの記事のタイトルです。2021.01.11
26行目のG(t)は、CAN-1-1-22-17のG(t)です。2021.01.13
27,28行目の右辺は、CAN-1-1-15-27~30に定義が書かれている全角運動量です。
それをL(t)と略記する事にする、というのがCAN-1-1-27-27,28の内容です。2021.01.13
29,30行目の等号の成立根拠は dri(t)/dt = ω(t)×ri(t) です。
dri(t)/dt = ω(t)×ri(t) の根拠は、CAN-1-1-26-2,3の式と B(t)r'i = ri(t) と G(t) = 0 です。
B(t)r'i = ri(t) の根拠は、CAN-1-1-22-17の式と G(t) = 0 です。
G(t) = 0 はCAN-1-1-27-26で仮定されています。2021.01.13,15;2021.06.12
【SEOテキスト】04.2.9,宇田雄一,第3章,質点系の力学,ω'2=,cosθsinψ+,cosψ,ω'3=,cosθcosψ-,sinψ,③Eulerの運動方程式,[慣性テンソル],(1)定義,剛体に固定された座標系(x''1-x''2-x''3系)で計った慣性テンソルI''は次式で定義される3×3行列である。,I''jk≡,n,∑,i=1,mi[|r''i|2δjk-rijrik],(2)主軸,x''=Ax',A∈SO(3)ならば、x'1-x'2-x'3系で計った慣性テンソルI'の成分は、,I'jk≡,n,∑,i=1,mi[|r'i|2δjk-r'ijr'ik]=,n,∑,i=1,mi[|A-1r''i|2δjk-(A-1r''i)j(A-1r''i)k]=(A-1)jlI''lsAsk,となる。,I''が実対称だから、I'が対称行列になるようにAを選ぶ事が出来る。そこで,I'=A-1I''A=Λ,Λjk=λjδjk,x''=Ax',A∈SO(3),とする。この時、x'1-x'2-x'3系の座標軸を主軸と呼ぶ。,[角運動量]G(t)=0の場合,L(t)≡,n,∑,i=1,miri(t)×,i(t)=,n,∑,i=1,miri(t)×[ω(t)×ri(t)]