
前のページ
目次
TEC-0-1-50
TEC-0-1-51
TEC-0-1-52
TEC-0-1-53
TEC-0-1-54
[補足説明欄]
1,2行目の等号の成立根拠は、ri(t)×[ω(t)×ri(t)] = [ri(t)・ri(t)]ω(t) - [ri(t)・ω(t)]ri(t) です。
[A×(B×C)]1 = A2(B×C)3 - A3(B×C)2
= A2(B1C2 - B2C1) - A3(B3C1 - B1C3)
= (A2C2 + A3C3)B1 - (A2B2 + A3B3)C1
= (A1C1 + A2C2 + A3C3)B1 - (A1B1 + A2B2 + A3B3)C1
= (A・C)B1 - (A・B)C1,
[A×(B×C)]2 = A3(B×C)1 - A1(B×C)3
= A3(B2C3 - B3C2) - A1(B1C2 - B2C1)
= (A3C3 + A1C1)B2 - (A3B3 + A1B1)C2
= (A1C1 + A2C2 + A3C3)B2 - (A1B1 + A2B2 + A3B3)C2
= (A・C)B2 - (A・B)C2,
[A×(B×C)]3 = A1(B×C)2 - A2(B×C)1
= A1(B3C1 - B1C3) - A2(B2C3 - B3C2)
= (A1C1 + A2C2)B3 - (A1B1 + A2B2)C3
= (A1C1 + A2C2 + A3C3)B3 - (A1B1 + A2B2 + A3B3)C3
= (A・C)B3 - (A・B)C3
∴ A×(B×C) = (A・C)B - (A・B)C.
この公式に A = ri(t), B = ω(t), C = ri(t) を代入すれば、
ri(t)×[ω(t)×ri(t)] = [ri(t)・ri(t)]ω(t) - [ri(t)・ω(t)]ri(t)
だと分かります。2021.02.02,05
3行目の等号の成立根拠は5,6行目の式です。
I(t)は(j, k)成分がIjk(t)である様な3×3行列です。
3行目のω(t)は、第k成分がωk(t)である様な3行1列の列ベクトルです。2021.02.02;2021.06.13
5,6行目のIjk(t)は、剛体に固定された座標系で測っての物ではないので、経時変化します。
それに対して、CAN-1-1-27-9,10のI''jkやCAN-1-1-27-14,15のI'jkは、剛体に固定された座標系で測っての物なので、経時変化しません。
この事が、Ijk(t)をIjkと書かなかった理由であり、I'jk, I''jkをI'jk(t), I''jk(t)と書かなかった理由です。2021.02.02,05
8行目の等号は定義です。2021.02.02
9行目の等号の成立根拠は L(t) = I(t)ω(t) です。
L(t) = I(t)ω(t) の根拠は、CAN-1-1-27-27からCAN-1-1-28-3までの計算の結果です。2021.02.02,05
10行目の左の等号の成立根拠は、I' = [B(t)]-1I(t)B(t) と ω'(t) = [B(t)]-1ω(t) です。
ω'(t) = [B(t)]-1ω(t) は、CAN-1-1-26-7の式です。
I' = [B(t)]-1I(t)B(t) は、CAN-1-1-27-14~18の計算と同様の計算で得られます。
|ri(t)|2 = ri(t)・ri(t) = [ri(t)]tri(t) = [B(t)r'i]tB(t)r'i = (r'i)t[B(t)]tB(t)r'i = (r'i)tr'i = r'i・r'i = |r'i|2 ・・・ (1)
∵ ri(t) = B(t)r'i ∵ CAN-1-1-22-17, CAN-1-1-27-26.
Σq=13[B(t)]qkriq(t) = Σq=13{[B(t)]t}kqriq(t) = Σq=13{[B(t)]-1}kqriq(t) = {[B(t)]-1ri(t)}k = r'ik ・・・ (2)
∵ r'i = [B(t)]-1ri(t) ・・・ (3).
{[B(t)]-1I(t)B(t)}jk
= Σp=13Σq=13 {[B(t)]-1}jpIpq(t)[B(t)]qk
= Σi=1n miΣp=13Σq=13 {[B(t)]-1}jp[|ri(t)|2δpq - rip(t)riq(t)][B(t)]qk ∵ CAN-1-1-28-5,6
= Σi=1n mi[|ri(t)|2Σp=13{[B(t)]-1}jp[B(t)]pk - Σp=13{[B(t)]-1}jprip(t)・Σq=13[B(t)]qkriq(t)]
= Σi=1n mi[|r'i|2δjk - r'ijr'ik] ∵ (1)(2)(3)
= I'jk ∵ CAN-1-1-27-14,15.
途中で随時 [B(t)]t = [B(t)]-1 (CAN-1-1-22-19への補足説明) を使いました。2021.02.02,03,04,05,06;2021.06.14,15
10行目の右の等号の成立根拠は I' = Λ (CAN-1-1-27-22) です。2021.02.02,05
11行目の[Eulerの運動方程式]は、11~26行目の記事のタイトルです。2021.02.02
12,13行目の式の根拠は、CAN-1-1-15-27,28の式とCAN-1-1-27-27,28の式です。
だから、CAN-1-1-15-24~26を見れば、Eulerの運動方程式は剛体の内力が作用反作用の法則に従いかつ中心力である事を前提にしていると分かります。
CAN-1-1-28-12,13の式は G(t) = 0 でなくても成り立ちます。2021.02.02,06,07;2021.06.14
14行目の等号の成立根拠は8行目の式です。2021.02.02
15行目の等号の成立根拠は L'(t) = Λω'(t) です。
L'(t) = Λω'(t) の根拠は、8~10行目に書かれています。2021.02.02,05
17行目の等号の成立根拠は [dB(t)/dt]Λω'(t) = ω(t)×[B(t)Λω'(t)] です。
[dB(t)/dt]Λω'(t) = ω(t)×[B(t)Λω'(t)] の成立根拠は、CAN-1-1-26-3の等号の成立根拠と同じです。2021.02.02,05
18行目の等号の成立根拠は ω(t)×[B(t)Λω'(t)] = B(t)[ω'(t)×Λω'(t)] です。
ω(t)×[B(t)Λω'(t)] = B(t)[ω'(t)×Λω'(t)] の成立根拠は、
ω(t) = B(t)ω'(t) と
[B(t)ω'(t)]×[B(t)Λω'(t)] = B(t)[ω'(t)×Λω'(t)] です。
[B(t)ω'(t)]×[B(t)Λω'(t)] = B(t)[ω'(t)×Λω'(t)] の成立根拠は、2つのベクトルを回転した後で外積しても外積した後で回転しても結果は変わらない事です。2021.02.02;2021.06.14
19行目の式の導出は次の様に行ないます。
まず、12,13行目の左の式に左から[B(t)]-1を掛けて
[B(t)]-1(d/dt)L(t) = [B(t)]-1N(t)
を得る。
この式に14~18行目の計算の結果を代入して25行目の式を使えば
ω'(t)×Λω'(t) + Λdω'(t)/dt = N'(t)
だと分かる。
この事と
ω'(t)×Λω'(t) = - [Λω'(t)]×ω'(t) ・・・ 外積の性質
から、
Λdω'(t)/dt - [Λω'(t)]×ω'(t) = N'(t)
だと分かります。2021.02.02;2021.06.14
21~23行目の式がEulerの運動方程式です。
21~23行目の式は、19行目の式にCAN-1-1-27-22の右の式で定義されている行列Λを代入すれば得られます。
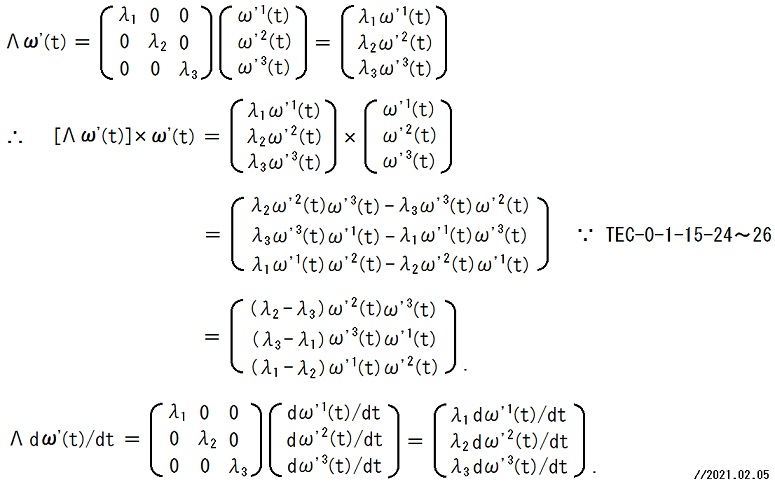
したがって、Λdω'(t)/dt - [Λω'(t)]×ω'(t) = N'(t) の成分は以下のごとくです。2021.02.02,05
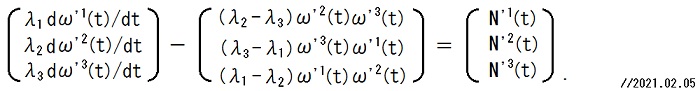
21~23行目のEulerの運動方程式を具体的な条件の下で解く事がTEC-0-1-50-6からTEC-0-1-54-13までで行なわれています。2021.06.15
27行目の[運動エネルギー]は、27~30行目の記事のタイトルです。2021.02.02
28,29行目の左の等号は定義であり、CAN-1-1-16-9,10の辺の[ ]内の前半をTと書く事にする、という意味です。
このTが剛体の運動エネルギーです。2021.02.06
28,29行目の右の等号の成立根拠は dri(t)/dt = ω(t)×ri(t) です。
|dri(t)/dt|2 = [dri(t)/dt]・[dri(t)/dt] = [ω(t)×ri(t)]・[ω(t)×ri(t)].
dri(t)/dt = ω(t)×ri(t) の根拠は、CAN-1-1-26-2,3の計算の結果と B(t)r'i = ri(t) と G(t) = 0 です。
B(t)r'i = ri(t) の根拠は、CAN-1-1-22-17の式と G(t) = 0 です。
G(t) = 0 はCAN-1-1-28-27で仮定されています。2021.02.03,06;2021.06.14
30行目の左の等号の成立根拠は以下です。
[ω(t)×ri(t)]・[ω(t)×ri(t)] = ω(t)・{ri(t)×[ω(t)×ri(t)]} ∵ (A×B)・C = A・(B×C)
= ω(t)・{[ri(t)・ri(t)]ω(t) - [ri(t)・ω(t)]ri(t)} ∵ A×(B×C) = (A・C)B - (A・B)C
= |ri(t)|2ω(t)・ω(t) - [ω(t)・ri(t)][ri(t)・ω(t)] ・・・ ここまでの式変形がTEC-0-1-54-16~18に書き出してある
= Σj=13Σk=13 ωj(t)[|ri(t)|2δjk - rij(t)rik(t)]ωk(t).
この事と5,6行目の式から、
[ω(t)]tI(t)ω(t) = Σj=13Σk=13 ωj(t)Ijk(t)ωk(t)
= Σi=1n miΣj=13Σk=13 ωj(t)[|ri(t)|2δjk - rij(t)rik(t)]ωk(t)
= Σi=1n mi[ω(t)×ri(t)]・[ω(t)×ri(t)].
2021.02.03,06,12
30行目の右の等号の成立根拠は以下です。
[ω(t)]tI(t)ω(t) = [B(t)ω'(t)]tI(t)B(t)ω'(t) ∵ CAN-1-1-26-7
= [ω'(t)]t[B(t)]tI(t)B(t)ω'(t)
= [ω'(t)]t[B(t)]-1I(t)B(t)ω'(t) ∵ [B(t)]t = [B(t)]-1 ∵ CAN-1-1-22-19
= [ω'(t)]tI'ω'(t) ∵ [B(t)]-1I(t)B(t) = I' (CAN-1-1-28-10への補足説明で導出されている)
= [ω'(t)]tΛω'(t) ∵ I' = Λ(CAN-1-1-27-22).
それだけではなく、Λjk = λjδjk (CAN-1-1-27-22) から、
[ω'(t)]tΛω'(t) = λ1[ω'1(t)]2 + λ2[ω'2(t)]2 + λ3[ω'3(t)]2
も言えます。2021.02.03,06,07,16;2021.06.14
【SEOテキスト】宇田雄一,04.2.10,第3章,質点系の力学,=,n,∑,i=1,mi{|ri(t)|2ω(t)-[ri(t)・ω(t)]ri(t)}=I(t)ω(t),ただし、,Ijk(t)≡,n,∑,i=1,mi[|ri(t)|2δjk-rij(t)rik(t)],さらに、,L'(t)≡[B(t)]-1L(t)=[B(t)]-1I(t)B(t)[B(t)]-1ω(t)=I'ω'(t)=Λω'(t),[Eulerの運動方程式]G(t)=0の場合、,d,-,dt,L(t)=N(t),N(t)≡,n,∑,i=1,ri(t)×Fi(t),(t)=(d/dt)[B(t)L'(t)]=(d/dt)[B(t)Λω'(t)]=,(t)Λω'(t)+B(t)Λdω'(t)/dt=ω(t)×[B(t)Λω'(t)]+B(t)Λdω'(t)/dt=B(t)[ω'(t)×Λω'(t)+Λdω'(t)/dt],∴Λdω'(t)/dt-[Λω'(t)]×ω'(t)=N'(t),すなわち、,{,λ1dω'1/dt-(λ2-λ3)ω'2ω'3=N'1,λ2dω'2/dt-(λ3-λ1)ω'3ω'1=N'2,λ3dω'3/dt-(λ1-λ2)ω'1ω'2=N'3,ただし、,N'(t)≡[B(t)]-1N(t),とする。,[運動エネルギー]G(t)=0の場合,T=,n,∑,i=1,mi,-,2,|,i(t)|2=,n,∑,i=1,mi,-,2,[ω(t)×ri(t)]・[ω(t)×ri(t)]=(1/2)[ω(t)]tI(t)ω(t)=(1/2)[ω'(t)]tΛω'(t)