
次のページ
前のページ
目次
CAN-1-1-26
CAN-1-1-28
TEC-0-1-18
[補足説明欄]
2行目の式の成立根拠はTEC-0-1-18-3〜5に書かれています。
ω1 = -Σk=13 B3kdB2k/dt = -Σk=13 B3k(dBt/dt)k2 = -(BdBt/dt)32,
ω2 = -Σk=13 B1kdB3k/dt = -Σk=13 B1k(dBt/dt)k3 = -(BdBt/dt)13,
ω3 = -Σk=13 B2kdB1k/dt = -Σk=13 B2k(dBt/dt)k1 = -(BdBt/dt)21.
2021.02.12
6行目の[問題45]は、TEC-0-1-50-6からTEC-0-1-54-13までの記事のタイトルです。
TEC-0-1-50-6〜20の内容が問題部分で、TEC-0-1-50-21〜TEC-0-1-54-13の内容が解答部分です。
TEC-0-1-50-21の「解」は、TEC-0-1-50-21〜TEC-0-1-54-13の記事のタイトルです。2021.02.07
8行目の λ1 = λ2 という条件は、対象とされている剛体がx'3軸のまわりの回転に対して対称である事を意味します。
その根拠として、主軸をx'3軸のまわりに回転させても λ1 = λ2 ならば慣性テンソルの成分が変化しない事、を以下に示します。

ある角度だけ回転した時に慣性テンソルの成分が回転前と同じに成る、というのではなく、回転角がどれだけであっても慣性テンソルの成分が回転前と同じに成るのだから、それは質点系(離散系)では無理、連続体でなければ λ1 = λ2 には成らないと思われます。
その意味で、ここで考えている問題45はCAN-1-1-28までで十分に基礎付けられていませんが、この様に質点系について成り立つ一般公式を連続体に流用する態度は、連続体の力学を発見する方法としてよく用いられ、体積分を使えば厳密に正当化され得るので妥当です。2021.02.07
9行目のMは、CAN-1-1-16-21,22で定義されているMで、剛体の全質量(剛体を構成する質点の質量の総合計)です。
9行目のgは、CAN-1-1-10-6で説明されている重力加速度です。2021.02.07
7〜9行目の右の式では
ri(t) ≠ 0 ⇒ Fi(t) = -migk ・・・ CAN-1-1-10-4〜7で説明されている重力(x3軸の負の向きだとする),
ri(t) = 0 ⇒ Fi(t) = -migk + (束縛力)
である場合を考えています。
N(t) = Σi=1n ri(t)×Fi(t) ∵ CAN-1-1-28-12,13
= -gΣi=1n miri(t)×k
= -gMrc×k ∵ CAN-1-1-16-21,22
= rc×(-Mgk).
重力が一様な場合を考えているので、重心と質量中心は一致しています。
rcの求め方は以下です。
7行目のlsinθsinφは、x'1 = 0, x'2 = 0, x'3 = l の点のx規約でのx1座標です。
8行目の-lsinθcosφは、x'1 = 0, x'2 = 0, x'3 = l の点のx規約でのx2座標です。
9行目のlcosθは、x'1 = 0, x'2 = 0, x'3 = l の点のx規約でのx3座標です。
その事は、CAN-1-1-22-17の式にCAN-1-1-23-16〜26の値と G(t) = 0 を代入すれば分かります。
xj = Bj1x'1 + Bj2x'2 + Bj3x'3
= (Bt)1jx'1 + (Bt)2jx'2 + (Bt)3jx'3
= (B-1)1jx'1 + (B-1)2jx'2 + (B-1)3jx'3
= (B-1)3jl.
G(t) = 0 とする理由は、今解こうとしている方程式がCAN-1-1-28-21〜23の方程式であり、この方程式は G(t) = 0 を前提としている(CAN-1-1-28-11)事です。
対象と成っている剛体の質量中心の位置を x'1 = 0, x'2 = 0, x'3 = l だとしています。
質量中心のx'1座標とx'2座標がどちらもゼロであるのは、対象と成っている剛体がx'3軸の周りの回転に対して対称だからです。2021.02.07;2021.06.16,18
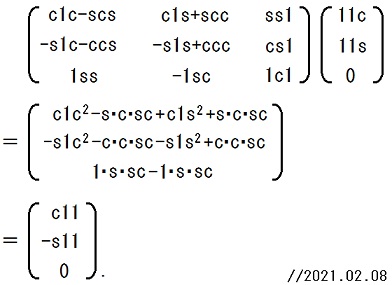
22行目の左の等号の成立根拠は、7〜9行目の右の式と列ベクトルの外積の定義(TEC-0-1-15-24〜26)です。2021.02.08
24行目の等号の成立根拠は、CAN-1-1-28-25の定義式です。2021.02.08
26行目の等号の成立根拠は、21〜23行目の計算の結果と、CAN-1-1-23-16〜26の内容です。
CAN-1-1-26の補足説明欄で使った略記法を使うと以下の様に計算できます。2021.02.08
【SEOテキスト】宇田雄一04.2.9,CAN-1-1-26-10,12,14,,20〜22,27〜29,ω1=-(BBt)32,ω2=-(BBt)13,ω3=-(BBt)21を使った方が計算が楽な場合には、これらを使っても良い。[問題45]x-規約を用いてλ1=λ2,N=(l sinθsinφ,-l sinθcosφ,l cosθ)×(0,0,-Mg)の場合のCAN-1-1-28-21〜23を解け。x'3,Mg,l,O,x'2,x'1,1点が固定された対称コマ,解:N=(Mgl sinθcosφ,Mgl sinθsinφ,0)=Mgl sinθ(cosφ,sinφ,0),N'=B-1 N=Mgl sinθ(cosψ,-sinψ,0)