次のページ
前のページ
目次
[補足説明欄]
1～3行目の式は、TEC-0-1-48-27～29の微分方程式の解です。
TEC-0-1-48-27～29への補足説明と同じ理由で、TEC-0-1-49-2,3の3k/2mは3k/(2m)です。
A1, A2, A3, φ1, φ2, φ3は積分定数です。2019.07.30;2020.12.07
4～6行目の式は、1～3行目の式の両辺に左からPを掛ける事によって得られます。
Pの成分はTEC-0-1-48-18～20に書かれています。2019.07.30;2020.12.07
7～9行目の式は、TEC-0-1-46-9～11の最も右の式です。
この式にTEC-0-1-49-4～6の式を代入すれば、y3, y5, y6 を求める事が出来ます。2019.07.30
10～19行目の図は、7～9行目の式、TEC-0-1-46-2の式、およびCAN-1-1-20-18～20の式の概念図です。2019.07.30
このページTEC-0-1-49は、19行目まで書いて「はい、出来た、後は4～6行目の式と10～19行目の図を見合わせながら自分の頭で P1, P2, P3 の運動を思い浮かべて下さい、出来るよね」という態度です。
後で読み返してみると、それでは不親切だ、という事が良く分かります。
だから、補足説明を以下に追記します。2019.08.02
4～6行目の式において、A1, A2, A3 の中のいずれか1つだけを非ゼロとし、残りの2つを両方ともゼロだとした場合の (⊿r1, ⊿r2, ⊿r3) と t の関係を「振動モード」と呼びます。
ω1 = √(3k/m), ω2 = √[3k/(2m)] として、7～9行目の式も使うと、
A1 ≠ 0, A2 = A3 = 0 で定義される振動モードは、
y1 = -(A1/√3)cos(ω1t + φ1),
y2 = (A1/√3)cos(ω1t + φ1),
y3 = -(A1/√3)cos(ω1t + φ1),
y4 = (A1/√3)cos(ω1t + φ1),
y5 = -(A1/√3)cos(ω1t + φ1),
y6 = (A1/√3)cos(ω1t + φ1).
これを第1振動モードと呼ぶ事にします。
A2 ≠ 0, A3 = A1 = 0 で定義される振動モードは、
y1 = (A2/√2)cos(ω2t + φ2),
y2 = (A2/√2)cos(ω2t + φ2),
y3 = -(A2/√2)cos(ω2t + φ2),
y4 = 0,
y5 = 0,
y6 = -(A2/√2)cos(ω2t + φ2).
これを第2振動モードと呼ぶ事にします。
A3 ≠ 0, A1 = A2 = 0 で定義される振動モードは、
y1 = (A3/√6)cos(ω2t + φ3),
y2 = -(A3/√6)cos(ω2t + φ3),
y3 = (A3/√6)cos(ω2t + φ3),
y4 = [A3√(2/3)]cos(ω2t + φ3),
y5 = -[A3√(2/3)]cos(ω2t + φ3),
y6 = -(A3/√6)cos(ω2t + φ3).
これを第3振動モードと呼ぶ事にします。
一般の振動については、Ai ≠ 0 ならば「その振動においては第 i 振動モードが励起されている」と言われます。
TEC-0-1-46-2に書かれている定義とCAN-1-1-20-2～20の内容を考え合わせると、上記の3つの振動モードは、以下の様に図示できます。
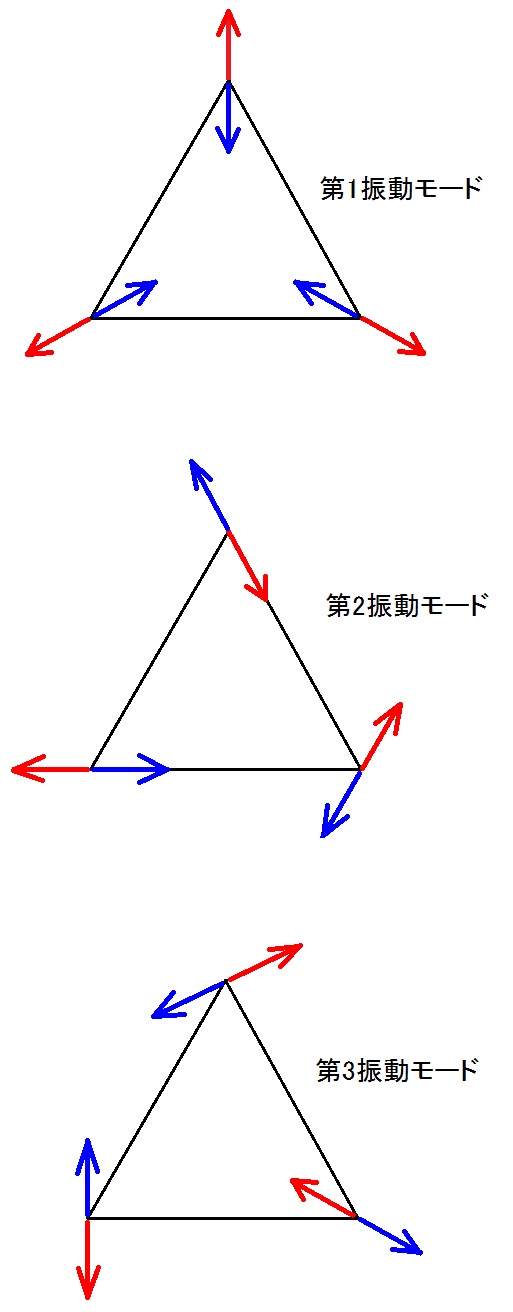2019.07.30TEC-0-1-49-10～19の図は、TEC-0-1-46-2やCAN-1-1-20-2～20を参照する為にページをめくらなくても、TEC-0-1-49-4～6の式から、これら3つの振動モードの図を思い描く事が出来る様にする為のメモです。2019.07.30;2019.08.02;2020.12.07
第2振動モードと第3振動モードは時間周期が等しいけれど、第1振動モードの時間周期は違います。
そのため、高校物理で習った「うなり」を思い出せば分かる様に、第1振動モードと他の振動モードが同時に励起されている場合には、各質点の振動状態は時間と共に変化します。
分かり難いかもしれないけれど、これは P1, P2, P3 だけで構成された質点系を媒質とする進行波を表現している、と解釈されてもよい事です。
各振動モードは高校物理で習った定常波に相当し、第2振動モードでは、y4 = y5 = 0 である事は、y4 と y5 が高校物理で習った定常波の節である事を意味します。
つまり、ここまでで扱った3質点系の問題は、弾性連続体中を伝わる波動(地震波をこれで近似できる)とか建築物や船体の固有振動といったテーマを扱う分野の中で最も簡単な問題だと見なせます。
したがって、ここまでで扱った3質点系の問題は、書道における永字八法の役割を、この分野において果たすでしょう。
ただし、当典には書かれていない面白いテクニックも、この分野には有ります。
個々の振動モードはいずれも定常波なのに複数の振動モードが同時に励起されると進行波が構成される事は、この分野の最大の見せ場のひとつでしょう。
加えて、CAN-1-1-12-25～CAN-1-1-13-5についての考察の結果を参考にするならば、建築物や船体のいずれかの振動モードの固有振動数に等しい振動数の外力は、建築物や船体の共振を引き起す、と推測できます。
その様な外力としては、建築物については地震が考えられ、船舶については推進用動力機関(エンジン)の振動が考えられます。
建築物は共振によって破損します。
また軍艦の光学式測距儀の設置環境には振動が少ない事が求められます。
化学の人にきいてみなければ分かりませんが、直接的な応用としては、3個の酸素原子Oで出来ているオゾン分子O3の性質を調べるのにTEC-0-1-49に書かれている結果を使う事が出来るのではないか、と思います。2019.08.02,04,09
【SEOテキスト】宇田雄一04.1.27,P-1 (y1 y2 y3)=(A1 cos(√ 3k/m t +φ1),A2 cos(√ 3k/m t +φ2),A3 cos(√ 3k/m t +φ3))∴(y1 y2 y4)=(-1/√3 1/√2 √ 1/6,1/√3 1/√2 -√ 1/6,1/√3 0 √ 2/3)(A1 cos(√ 3k/m t +φ1),A2 cos(√ 3k/m t +φ2),A3 cos(√ 3k/m t +φ3)),(y3 y5 y6)=(0 -1 0,0 0 -1,-1 0 0)(y1 y2 y4),y6=-y1,-y4=y5,y1,y4,y3=-y2,y2