次のページ
前のページ
目次
CAN-1-1-21
[補足説明欄]
3〜8行目の式は、CAN-1-1-21-8〜13の式を行列形式に書き直した物です。
ただし、TEC-0-1-46-2に書かれている様な、変数の名称変更、を前提としています。2019.07.29
9〜11行目の最も左の式の成立根拠は、CAN-1-1-21-21,22,24の式です。
CAN-1-1-21-21の式から、
(x12 + x21) - (x23 + x32) = 0
∴ x12 + x21 = x23 + x32 ・・・ (1)
CAN-1-1-21-22の式から、
(x13 + x31) - (x23 + x32) = 0
∴ x13 + x31 = x23 + x32 ・・・ (2)
CAN-1-1-21-24の式から、
(x12 + x21) + (x13 + x31) + (x23 + x32) = 0 ・・・ (3)
式(1)(2)を式(3)に代入すると、
3(x23 + x32) = 0
∴ x23 + x32 = 0 ・・・ (4)
この事と式(1)(2)より、
x12 + x21 = x13 + x31 = 0 ・・・ (5)
以上を見れば、ここまでの計算は暗算で出来る事、が分かるでしょう。
だから私はTEC-0-1-46-9〜11の最も左の式を書く際には暗算で済ませています。
式(4)(5)はTEC-0-1-46-9〜11の最も左の式です。2019.07.29
9〜11行目の最も右の式を導出できた時点で、微分方程式を(y1, y2, y4)だけについての形に変形できる事が約束されました。
よって、ここ以降は、まず微分方程式を解いて(y1, y2, y4)を求め、その結果を9〜11行目の最も右の式に代入して(y3, y5, y6)を得よう、という計画の実行です。2019.07.29
13行目の等号の成立は、3〜8行目の式の両辺の行列の行の意味での第1,2,4行目に着目すれば分かります。2019.07.29
18行目の縦等号の成立根拠は以下です。2019.07.29
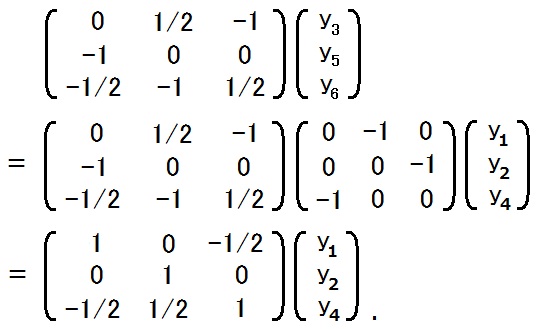2019.07.2927,28行目について。
もし M が対称行列に成らなかったなら、対角化出来ないので対角化を使った解法を使えなかったところですが、ここで M が対称行列に成ったのは偶然ではありません。
M が対称行列に成ったのは、三つのバネが皆等しいからでも、三つの質点の質量が皆等しいからでも、ありません。
仮にこれらが等しくなかったとしても、対角化を使った解法は有効です。
連結微小振動の問題は、常に対角化を使って解く事が出来ます。
当初等力学正典では、何故そうなのかを証明しませんが、たとえば、ゴールドスタイン著「新版・古典力学（上）」吉岡書店
の第 6-1 節を見れば、何故そうなのかが分かります。実対称行列はどれも対角化可能である事の証明は、例えば、マグロウヒル大学演習シリーズ「線形代数(下)」リプシュッツ著加藤明史訳358ページに演習問題13.32として書かれています。
そこでは線形作用素の言葉で証明が書かれているので、以下にそれを行列の言葉で書き直しておきます。2008.08.01,06;2021.01.17,18,20
Mを実対称N×N行列とする。
N = 1の場合には、Mは元々対角行列だから対角化可能である事は自明です。
N = nの場合にMが対角化可能ならばN = n+1の場合にもMは対角化可能である事、を示せば数学的帰納法によって一般のNに対してMが対角化可能である事を証明できた事に成るので、そうします。
N = n+1の場合、Mvn+1 = λn+1vn+1, vj・vk = δjk,
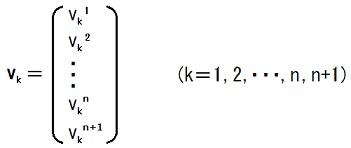
である様な実数λn+1と実列ベクトルv1, v2, ・・・, vn, vn+1が存在する(※1)。
P = (v1 v2 ・・・ vn vn+1)
とする。
Pは、第k列がvkである様な(n+1)×(n+1)行列です。
PtMP ＝ (v1 v2 ・・・ vn vn+1)tM(v1 v2 ・・・ vn vn+1)
＝ (v1 v2 ・・・ vn vn+1)t(Mv1 Mv2 ・・・ Mvn Mvn+1)
このうちで
v1・Mvn+1 = v2・Mvn+1 = ・・・ = vn・Mvn+1 = 0 ・・・ ※2
vn+1・Mv1 = vn+1・Mv2 = ・・・ = vn+1・Mvn = 0 ・・・ ※3
vn+1・Mvn+1 = λn+1 ・・・ ※4
だから、
このうちで
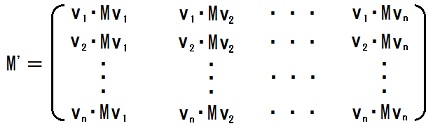
は実対称n×n行列だ(※5)から、数学的帰納法の仮定により、対角化可能です。
Q'を実n×n行列とし、λ1, λ2, ・・・, λnを実数として、
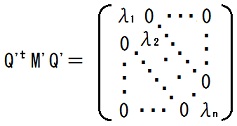
だとする。
ここで(n + 1)×(n + 1)行列Qを
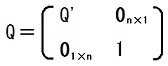
で定義すると、
(PQ)tM(PQ) ＝ Qt(PtMP)Q
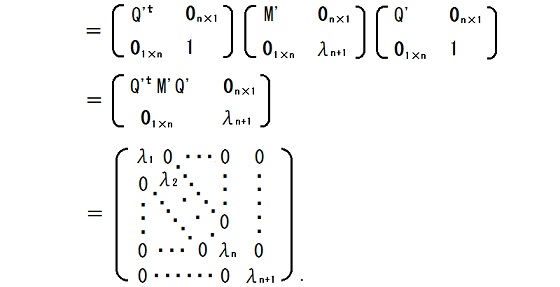
ただし、0n×1はn行1列のゼロ行列、01×nは1行n列のゼロ行列です。
※1の根拠は、以下です。
λについての方程式 |M - λ1n+1| = 0 は、1変数の代数方程式だから、複素数の範囲内に必ず解を少なくとも1つは持つ(∵代数学の基本定理)。
|M - λ1n+1| は M - λ1n+1 の行列式です。1n+1はn+1行n+1列の単位行列です。
λ = λn+1 を |M - λ1n+1| = 0 の解だとする。
すると、λn+1は、実対称行列Mの固有値だ(※6)から、実数だ(※7)。
Mvn+1 = λn+1vn+1
は、vn+11, vn+12, ・・・, vn+1n, vn+1n+1についての実係数の連立1次方程式だから、その解としては|vn+1|=1である様な実列ベクトルvn+1を選べる(※8)。
このvn+1に対して、{v1, v2, ・・・, vn, vn+1}が規格直交集合に成る様にn個の実列ベクトルv1, v2, ・・・, vnを補う事が必ず出来る(※9)。
※4の根拠は、vn+1・Mvn+1 = vn+1・(λn+1vn+1) = λn+1vn+1・vn+1 and vn+1・vn+1= δn+1, n+1 = 1 です。
※2の根拠は、vk・Mvn+1 = vk・(λn+1vn+1) = λn+1vk・vn+1 and vk・vn+1 = δk, n+1 です。
※3の根拠は、vn+1・Mvk = vn+1tMvk = (vn+1tMvk)t = vktMtvn+1 = vktMvn+1 = vk・Mvn+1 および※2です。
この推論の途中では、1×1行列は転置しても変わらない事と、Mt = M を、使いました。
Mt = M の根拠は、Mが対称行列である事です。
※5の根拠は、vj・Mvk = vjtMvk = (vjtMvk)t = vktMtvj = vktMvj = vk・Mvj です。
※6の根拠は以下です。
Mvn+1 = λn+1vn+1 はvn+11, vn+12, ・・・, vn+1n, vn+1n+1についての連立1次方程式であり、その中の独立な方程式の個数はn+1個より少ない。
なぜなら、 Mvn+1 = λn+1vn+1 は (M - λn+11n+1)vn+1 = 0 と同じであり、|M - λn+11n+1| = 0 だからです。
もし、M - λn+11n+1の逆行列(M - λn+11n+1)-1が存在するならば、
(M - λn+11n+1)-1(M - λn+11n+1) = 1n+1
∴ |(M - λn+11n+1)-1|×|M - λn+11n+1| = |1n+1| = 1.
しかし、これは |M - λn+11n+1| = 0 に反するから、M - λn+11n+1の逆行列は存在しません。
M - λn+11n+1の逆行列が存在しないという事は、(M - λn+11n+1)vn+1 = 0 の中の独立な方程式の個数がn+1個より少ないという事です(※10)。
変数はvn+11, vn+12, ・・・, vn+1n, vn+1n+1のn+1個なのに、独立な方程式の個数はn+1個より少ないので、 Mvn+1 = λn+1vn+1 は必ず vn+1 ≠ 0 である様な解を持つ。
※7の根拠は、実対称行列の固有値はどれも必ず実数である事、です。
実対称行列の固有値がどれも必ず実数である事の根拠は以下です。
Mv = λv, v ≠ 0 ならば
v*tv = Σk=1n+1 |vk|2 ≠0,
(λ* - λ)v*tv = λ*v*tv - λv*tv = (Mv)*tv - v*tMv = v*tM*tv - v*tMv = v*t(M*t - M)v = 0
∵ M*t = M ・・・ Mは実対称。
*は複素共役です。
※8の根拠は以下です。
Mvn+1 = λn+1vn+1 はvn+11, vn+12, ・・・, vn+1n, vn+1n+1についての連立1次方程式であり、その中の独立な方程式の個数はn+1個より少ない(※6の根拠)。
この事とλn+1が実数である事(※7)とMが実行列である事を考え合わせると、Mvn+1 = λn+1vn+1 は必ず vn+1 ≠ 0 である様な実列ベクトルを解に持つ、と分かります。
v'n+1がその様な解ならば、vn+1 = v'n+1/|v'n+1| は、実列ベクトルであり、|vn+1| = 1 である様な解です。
※9の根拠は以下です。
まず、与えられた実列ベクトルvn+1に対して、vn+1・vn = 0 and |vn| = 1 である様な実列ベクトルvnが必ず存在する。
なぜなら、vn+1・vn = 0 という方程式は、vn1, vn2, ・・・, vnn, vnn+1についての実係数の1次方程式だからです。
vn+11vn1 + vn+12vn2 + ・・・ + vn+1nvnn + vn+1n+1vnn+1 = 0.
この方程式は必ず vn ≠ 0 である様な実列ベクトルを解に持つ。
例えば、vn+1n+1≠0 ならば vn1 = vn2 = ・・・ = vnn = 1 and vnn+1 = -(vn+11 + vn+12 + ・・・ + vn+1n)÷vn+1n+1 が、vn+1n+1 = 0 ならば vn1 = vn2 = ・・・ = vnn = 0 and vnn+1 = 1 が、その様な解です。
v'nがその様な解ならば、vn = v'n/|v'n| は、実列ベクトルであり、|vn| = 1 である様な解です。
一般に、(n+1)-k個の実列ベクトルvk+1, ・・・, vn, vn+1が与えられた時、vk・vk+1 = ・・・ = vk・vn = vk・vn+1 = 0 and |vk| = 1 である様な実列ベクトルvkが必ず存在する。
なぜなら、vk・vk+1 = ・・・ = vk・vn = vk・vn+1 = 0 という方程式は、vk1, vk2, ・・・, vkn, vkn+1についての実係数の連立1次方程式だからです。
vk+11vk1 + vk+12vk2 + ・・・ + vk+1nvkn + vk+1n+1vkn+1 = 0,
・
・
・
vn1vk1 + vn2vk2 + ・・・ + vnnvkn + vnn+1vkn+1 = 0,
vn+11vk1 + vn+12vk2 + ・・・ + vn+1nvkn + vn+1n+1vkn+1 = 0.
この方程式は必ず vk ≠ 0 である様な実列ベクトルを解に持ちます。
なぜなら、変数はvk1, vk2, ・・・, vkn, vkn+1のn+1個なのに、方程式の個数は(n+1)-k個であり、これはn+1個より少ないからです。
v'kがその様な解ならば、vk = v'k/|v'k| は、実列ベクトルであり、|vk| = 1 である様な解です。
数学の解説を始めるとキリが無いので、本当は数学については数学の解説サイトや解説書で読んで欲しいけれど、せっかくだから、逆行列の存在と独立な方程式の個数の関係(※10)の証明を以下に書いておきます。
ああ、誰か、数学正典というタイトルで数学の解説記事を書いてくれないかな。2021.01.18,20,22,23,24,25,26,27,28,29,30,31;2021.02.01,02
Pを与えられた実N×N行列とし、aをN行1列の与えられた実列ベクトルとし、N行1列の列ベクトルxについての Px = a という方程式を考えます。
この方程式は以下の連立方程式を行列の言葉で書いた物です。
P11x1 + P12x2 + ・・・ + P1NxN = a1,
P21x1 + P22x2 + ・・・ + P2NxN = a2,
・
・
・
PN1x1 + PN2x2 + ・・・ + PNNxN = aN.
この連立方程式の中の独立な方程式の個数がNならば、解は1個だけなので、それを x = F(a) とします。
この列ベクトル値関数Fは以下の性質を持ちます。
F(a1 + a2) = F(a1) + F(a2) and F(ca) = cF(a) ・・・ ※11
この様な性質を線形性と言います。cは任意の実数です。
だから、第j成分がδjkである(第k成分のみ1でそれ以外は全てゼロである)様なN行1列の列ベクトルをδ□kと書けば、
F(a) ＝ F(a1δ□1 + a2δ□2 + ・・・ + aNδ□N) ∵ a = a1δ□1 + a2δ□2 + ・・・ + aNδ□N
＝ F(a1δ□1) + F(a2δ□2) + ・・・ + F(aNδ□N)
＝ a1F(δ□1) + a2F(δ□2) + ・・・ + aNF(δ□N)
この最後の式の最右辺のN×N行列をSと書けば、x = F(a) = Sa が Px = a の唯一の解なのだから、
PSa = a ・・・ (1)
これが任意のaに対して成り立つのだから、
PS = 1N ・・・ (2)
また、(1)の両辺に左からSを掛ければ、
SP(Sa) = Sa
ですが、どんな列ベクトルも必ずSaの形に書ける(※12)から、
SP = 1N ・・・ (3)
(2)(3)より、
S = P-1.
これで、独立な方程式の個数がNならばPの逆行列が存在する事、が証明されました。
逆に、Pの逆行列P-1が存在するならば、Px = a の両辺に左からP-1を掛ければ、x = P-1a が唯一の解だと分かるので、独立な方程式の個数はN個です。
なぜなら、独立な方程式の個数がN個より少なければ、解は1個よりも多く成るからです。
※11は、Px = a1 + a2 の解は x = F(a1) + F(a2) だけであり、Px = ca の解は x = cF(a) だけである事を意味します。
※11が正しい事は、x = F(a1) + F(a2) を Px = a1 + a2 に代入したり、x = cF(a) を Px = ca に代入したりして確認できます。
P[F(a1) + F(a2)] = PF(a1) + PF(a2) = a1 + a2,
P[cF(a)] = cPF(a) = ca.
独立な方程式の個数は、Px = a と Px = a1 + a2 と Px = ca で同じだから、Px = a の解が1つだけなら Px = a1 + a2 や Px = ca の解も1つだけです。
※12の根拠は以下です。
第j成分がSjkである様な列ベクトルをS□kと書く事にすると、
Sa = a1S□1 + a2S□2 + ・・・ + aNS□N.
この事とS□1, S□2, ・・・, S□Nが線形独立である事から※12が言えます(※13)。
S□1, S□2, ・・・, S□Nが線形独立である事は、(1)が任意のaに対して成り立つ事によって保証されています。
(1)に Sa = a1S□1 + a2S□2 + ・・・ + aNS□N を代入すると、
P(a1S□1 + a2S□2 + ・・・ + aNS□N) = a
ですが、
P(a1S□1 + a2S□2 + ・・・ + aNS□N) = a1PS□1 + a2PS□2 + ・・・ + aNPS□N
なので、
a1PS□1 + a2PS□2 + ・・・ + aNPS□N = a.
これが任意のaに対して成り立つのだから、
PS□1 = δ□1 and PS□2 = δ□2 and ・・・ and PS□N = δ□N.
このうちでδ□1, δ□2, ・・・, δ□NはN個の線形独立なベクトルだし、Pを作用させる事で線形独立なベクトルの個数は変わらないかまたは減るだけで増える事は無いので、S□1, S□2, ・・・, S□NもN個の線形独立なベクトルです。
この事情を以下に詳しく書いておきます。
Pu1, Pu2, ・・・, PuNは線形独立だとする。
a1u1 + a2u2 + ・・・ + aNuN = 0 ならば a1Pu1 + a2Pu2 + ・・・ + aNPuN = P(a1u1 + a2u2 + ・・・ + aNuN) = P0 = 0.
ところがPu1, Pu2, ・・・, PuNは線形独立なので、a1Pu1 + a2Pu2 + ・・・ + aNPuN = 0 ならば a = 0 です。
したがって、a1u1 + a2u2 + ・・・ + aNuN = 0 ならば a = 0 です。
これはu1, u2, ・・・, uNが線形独立である事に他なりません。
今の場合は、a1S□1 + a2S□2 + ・・・ + aNS□N = 0 ならば、
a = a1PS□1 + a2PS□2 + ・・・ + aNPS□N = P(a1S□1 + a2S□2 + ・・・ + aNS□N) = P0 = 0
と考える事も出来ます。
※13の根拠をまだ書いていませんが、それを言うなら、方程式の個数が変数の個数より少なければ非ゼロ解が存在する理由もまだ書いていません。
物理学の学習ではこれらを証明なしで使ってもよいけれど、数学の本に書かれていた証明が教訓的だったので、以下でそれを紹介します。2021.01.26,27,28,30,31;2021.02.02
※13を証明するに当たっては、証明の途中で根拠として※12を使わない様にする等の注意が必要です。
※13は※12の証明の途中で根拠として使われているので、※13の証明の途中で根拠として※12を使えば、循環論法とか論点先取と呼ばれる詭弁に成ってしまい、※13の証明も※12の証明も成立しません。
「あなたは精神病だから言ってる事が間違ってるから精神病です」こういうのが循環論法です。
本当は、支離滅裂とか意味不明とは、こういう言説の事であるはずです。
※13の根拠は、例えば、マグロウヒル大学演習シリーズ「線形代数(上)」リプシュッツ著加藤明史訳の104ページに補題5.4として書かれており、この補題の証明が演習問題5.14として116ページに書かれています。
N行1列の実列ベクトル全体の集合をVとします。
すると、Vはδ□1, δ□2, ・・・, δ□Nの線形結合全体の集合です。
この事を、{δ□1, δ□2, ・・・, δ□N}はVを生成する、と言います。
{δ□1, δ□2, ・・・, δ□N}はVを生成するので、{S□1, δ□1, δ□2, ・・・, δ□N}は線形従属でありかつVを生成します。
だから、{S□1, δ□1, δ□2, ・・・, δ□N}で自分よりも左に書かれているベクトルの線形結合で表されるベクトルがδ□1, δ□2, ・・・, δ□Nの中に必ず存在し(※14)、そのベクトルを{S□1, δ□1, δ□2, ・・・, δ□N}から削除して得られる集合もVを生成する(※15)。
そうして得られた集合を{S□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)}とする。
すると、{S□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)}はVを生成するので、{S□2, S□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)}は線形従属でありかつVを生成する。
だから、{S□2, S□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)}で自分よりも左に書かれているベクトルの線形結合で表されるベクトルがS□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)の中に必ず存在し、そのベクトルを{S□2, S□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)}から削除して得られる集合もVを生成するが、S□1がS□2の線形結合で表される事は無い(∵S□1, S□2, ・・・, S□Nは線形独立)ので、削除されるのはδ□p(1), δ□p(2), ・・・, δ□p(N-1)のうちのいずれかです。
削除して得られた集合を{S□2, S□1, δ□q(1), δ□q(2), ・・・, δ□q(N-2)}とする。
同様の作業を繰り返す事により、{S□N, ・・・, S□2, S□1}はVを生成する事、が分かる。
S□1, S□2, ・・・, S□Nは線形独立だから、・・・, S□2, S□1のうちのいずれのベクトルも自分より左に書かれているベクトルの線形結合ではなく、その為に、この作業の途中でS□1, S□2, ・・・, S□Nのいずれも削除される事は有りません。
※14の根拠は以下です。
まず、{δ□1, δ□2, ・・・, δ□N}も線形独立だし{S□1, S□2, ・・・, S□N}も線形独立だから、δ□1, δ□2, ・・・, δ□N, S□1, S□2, ・・・, S□Nのいずれもゼロベクトルではない。
u1, u2, ・・・, unは線形従属であり、いずれもゼロベクトルではないとする。
すると、線形従属性の定義によって、
c1u1+ c2u2 + ・・・ + cnun = 0 and not(c1 = c2 = ・・・ = cn = 0)
である様なn個の実数c1, c2, ・・・, cnが存在する。
c1, c2, ・・・, cnのうちのゼロでない物のうちで最も右に書かれている物はckだとする。
すると、j ＞ k ならば cj = 0 だから、
c1u1+ c2u2 + ・・・ + ckuk = 0.
ここで、もし k = 1 だとすると、c1u1 = 0 and c1 ≠ 0 ∴ u1 = 0
である事に成ってしまうが、これはu1がゼロベクトルではない事と矛盾するので k ＞ 1.
∴ uk = (-c1/ck)u1 + (-c2/ck)u2 + ・・・ + (-ck-1/ck)uk-1.
※15の根拠は、以下です。
削除されたベクトルをS□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)の線形結合で表す式を、S□1, δ□1, δ□2, ・・・, δ□Nの任意の線形結合の式に代入すれば、S□1, δ□1, δ□2, ・・・, δ□Nのどんな線形結合もS□1, δ□p(1), δ□p(2), ・・・, δ□p(N-1)の線形結合で表される、と分かる。
さて、※13の根拠は、線形独立なN個の実列ベクトルからなる集合はどれもN行1列の実列ベクトル全体の集合を生成する事ですが、物理学では3次元空間内の独立な3つの矢印ベクトルを思い浮かべてそれからの類推で「まあそうだわな」で済ませても構わないこの定理も、その証明が思ったほど簡単ではない事は、物理学への戒めとして教訓的です。
δ□1, δ□2, ・・・, δ□NのそれぞれをS□1, S□2, ・・・, S□Nのいずれかに1つずつ置き換えて行く事が出来る、という証明の骨子は単純明快なのですが、私は気付かなかったなあ。2021.01.30,31;2021.02.01,02
次ページ以降に、このページの記事の続きが書かれています。2019.07.30
【SEOテキスト】宇田雄一04.1.27,CAN-1-1-21-8〜13,21,22,24,y1≡x31,y2≡x32,y3≡x23,y4≡x21,y5≡x12,y6≡x13,m(y1 y2 y3 y4 y5 y6)=-k(1 -1/2 0 0 1/2 -1,-1/2 1 -1 1/2 0 0,1/2 -1 1 -1/2 0 0,0 0 -1/2 1 -1 1/2,0 0 1/2 -1 1 -1/2,-1 1/2 0 0 -1/2 1)(y1 y2 y3 y4 y5 y6),x23+x32=0∴y2+y3=0,x12+x21=0∴y4+y5=0,x13+x31=0∴y1+y6=0,(y3 y5 y6)=(0 -1 0,0 0 -1,-1 0 0)(y1 y2 y4),m(y1 y2 y4)=-k(1 -1/2 0,-1/2 1 1/2,0 0 1)(y1 y2 y4)-k(0 1/2 -1,-1 0 0,-1/2 -1 1/2)(y3 y5 y6),=(1 0 -1/2,0 1 0,-1/2 1/2 1)(y1 y2 y4),=-k(2 -1/2 -1/2,-1/2 2 1/2,-1/2 1/2 2)(y1 y2 y4),=M,Mは実対称だから、固有ベクトルを基底とする表現では対角行列となる。