
次のページ
前のページ
目次
[補足説明欄]
1行目の式の成立根拠は、TEC-0-1-47-28〜30の式です。
TEC-0-1-47-28〜30の式からは、TEC-0-1-48-1の式と独立な式は得られません。
TEC-0-1-47-14〜16の式から得られる独立な式の個数とTEC-0-1-47-28〜30の式から得られる独立な式の個数が異なる事は、TEC-0-1-47-11の式の左辺で(λ-3)の冪と(2λ-3)の冪が異なる事に対応しています。2020.12.06
2〜4行目に書かれているのは、x = y + z である様な2つの列ベクトルです。
これらがMの固有値3/2に属する固有空間の基底だ、と置いています。
x = y + z の根拠は1行目の式です。2020.12.06
7行目では、y1の値とz1の値を自由に選べる事を使っています。
ただし、(y1 + z1, y1, z1)が単位ベクトルに成る様にy1の値とz1の値を選んでいます。2020.12.06
(y1 + z1)2 + y12 + z12 = 1.
8行目の式は、7行目の値を6行目の式に代入する事によって得られます。2020.12.06
12行目の等号の成立根拠は、9行目の式です。2020.12.06
14〜16行目の式の右辺には、2〜4行目の2つの列ベクトルが書かれています。
TEC-0-1-47-28〜30の式の解は、無限個あり、これら2つだけではありませんが、どんな解も、これら2つの列ベクトルの線形結合です。
また、これら2つの列ベクトルのどんな線形結合も解です。
TEC-0-1-47-24〜26に対する補足説明と同様の理由で、TEC-0-1-48-13の2つの値 z2 = +√(2/3), -√(2/3) のうちから z2 = +√(2/3) を選んでいます。2020.12.06
14〜16行目の答えとしても、Mの固有値3/2に属する固有空間の基底なら何でも良く、直交性を課す事(5行目)も規格化する事(10行目)も必要では有りません。
答えの列ベクトルが2つに成ってしまった事は、Mの固有値3/2に属する固有空間が2次元である事を意味し、TEC-0-1-47-11の第2因子が2乗されている事に由来します。
この様に1つの固有値に属する固有空間の次元が1よりも大きく成る事、を「縮退」と呼びます。
私は証明しませんが、系の対称性は縮退を生じさせる、と言われます。
今扱っている問題の場合は、3つのバネが長さもバネ定数も全て等しく、かつ3つの質点の質量が全て等しい、こういうのが系の対称性です。
18〜20行目の行列の内容は、TEC-0-1-47-24〜26の列ベクトルとTEC-0-1-48-14〜16の列ベクトルを並べただけです。
こうすれば良い事は、数学から習いました。
ここで用いられる列ベクトルは規格化や直交化をされている必要が有ります。
21〜23行目で、対角化が成功している事が確認できたので、物理学としては、何故その方法で対角化できたのか知る必要は無い、という面が有ります。
しかし、大学1年生の数学なので、一応説明しておきます。
まず、行列の積の定義を思い出して下さい。
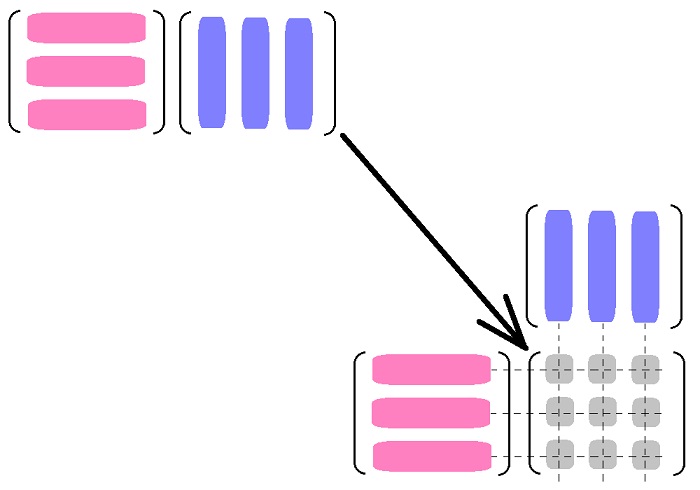
この様に、左の行列の行ベクトルと右の行列の列ベクトルの内積が、積行列の要素に成るのでした。
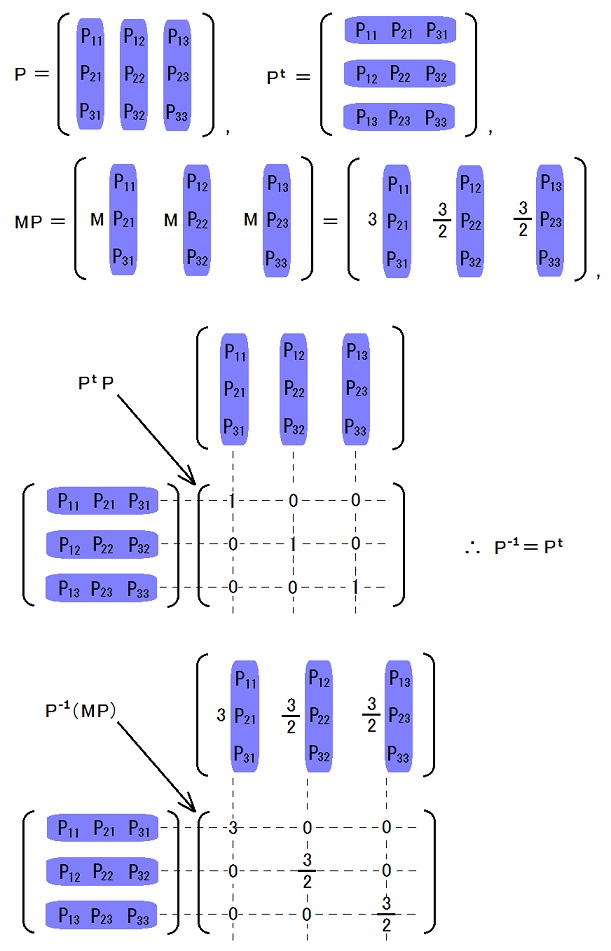
この事から、列ベクトルがどれも規格化されており互いに直交している行列の逆行列は転置行列に等しい事が分かるので、以下では、その事を使います。
P内の列ベクトルのうちで、固有値3/2に属する2つの列ベクトルが互いに直交する事は、5,6行目の条件によって保証されています。
固有値3に属する列ベクトルも固有値3/2に属する列ベクトルに直交しますが、これは異なる固有値に属するベクトルは互いに直交するからです。
Mt = M and Mx = λx and My = μy ⇒ (λ - μ)xty = (λx)ty - xt(μy) = (Mx)ty - xtMy = xt(Mt - M)y = 0
∴ λ≠μ ⇒ xty = 0.
 .2019.07.29;2019.08.02,05,06,14
.2019.07.29;2019.08.02,05,06,1424〜26行目の式は、TEC-0-1-46-12〜24の式の両辺に左からP-1を掛ける事によって得られます。
TEC-0-1-48-25のPP-1は単位行列に等しい事、に注意して下さい。2019.07.29;2020.12.06
27〜29行目の式は、24〜26行目の式に21〜23行目の行列を代入する事によって得られます。
だから、28,29行目の-3k/2mは-(3k/2)mではなく-3k/(2m)です。2020.12.06
次ページに、このページの記事の続きが書かれています。2019.07.30
【SEOテキスト】宇田雄一04.1.27,x-y-z=0,(y1+z1 y1 z1),(y2+z2 y2 z2)直交性を課すと、(y1+z1)(y2+z2)+y1y2+z1z2=0,y1=1/√2,z1=0とすると(y2+z2)/√2+y2/√2=0∴y2=-z2/2規格化すると1=(y2+z2)2+(y2)2+(z2)2=3(z2)2 /2∴|z2|=√ 2/3,(x y z)=(1/√2 1/√2 0),(√ 1/6 -√ 1/6 √ 2/3)従ってMを対角化する行列は、P=(-1/√3 1/√2 √ 1/6,1/√3 1/√2 -√ 1/6,1/√3 0 √ 2/3),P-1 MP=(3 0 0,0 3/2 0,0 0 3/2),mP-1(y1 y2 y4)=-k P-1 MP P-1 (y1 y2 y4),P-1 (y1 y2 y4)=(-3k/m 0 0,0 -3k/ 2m 0,0 0 -3k/ 2m) P-1 (y1 y2 y4)